���σx�N�g���E���σx�N�g���E���σe���\���E���σe���\��
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
K�n�̐��E�_x���A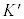 �n�ɍ��W�ϊ�����Đ��E�_
�n�ɍ��W�ϊ�����Đ��E�_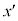 �ɂȂ����Ƃ��܂��B
�ɂȂ����Ƃ��܂��B
K�n�ɂ������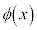 �̒l��
�̒l��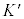 �n�ɂ������
�n�ɂ������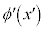 �̒l���������Ƃ��A�����A
�̒l���������Ƃ��A�����A
�ƂȂ�Ƃ��Aϕ���X�J���[�ƌ����܂��B
�A���藝���A
�k�����ď����ƁA
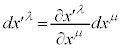 �@(����ɗ��Ă���
�@(����ɗ��Ă���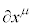 �̓Y��μ�͉��t���Y���̂悤�ɍl���Ă�������)
�̓Y��μ�͉��t���Y���̂悤�ɍl���Ă�������)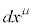 �̓Y��μ����ɏ����Ƃ��܂������̂ł��B���W
�̓Y��μ����ɏ����Ƃ��܂������̂ł��B���W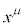 �̓Y��μ����ɏ����܂��B�܂��A���W�ϊ�
�̓Y��μ����ɏ����܂��B�܂��A���W�ϊ�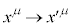 �ɑ��āA
�ɑ��āA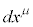 �Ɠ��l�̕ϊ��̎d��������x�N�g��
�Ɠ��l�̕ϊ��̎d��������x�N�g��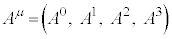 �C�܂�A
�C�܂�A
�̂悤�ɕϊ������x�N�g�������σx�N�g���ƌ����܂��B���σx�N�g���̐����̓Y���͉E��ɏ����܂��B�ׂ���̎w���ƕ���킵���̂Œ��ӂ��Ă��������B
����ɑ��A�X�J���[ϕ���e���W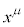 �Ŕ������Ăł���x�N�g��(4���Igrad�Ƃ����������)
�Ŕ������Ăł���x�N�g��(4���Igrad�Ƃ����������)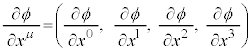 �́A�A���藝���A
�́A�A���藝���A
�k�ď����ƁA
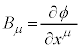 (�E�ӂ̓Y��μ�͕���ɂ���̂ʼn��t������)�Ə����ƁA
(�E�ӂ̓Y��μ�͕���ɂ���̂ʼn��t������)�Ə����ƁA
���̂悤�ɕϊ������x�N�g��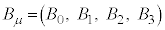 �����σx�N�g���ƌ����܂��B���σx�N�g���̐����̓Y���͉E���ɏ����܂��B
�����σx�N�g���ƌ����܂��B���σx�N�g���̐����̓Y���͉E���ɏ����܂��B
K�n�ō��W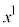 �̖ڐ����1m��1�C2m��2�ƂȂ�悤�Ɏ���Ă����̂��A
�̖ڐ����1m��1�C2m��2�ƂȂ�悤�Ɏ���Ă����̂��A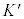 �n�ō��W
�n�ō��W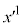 �̖ڐ����2m��1�C4m��2�ƂȂ�悤�Ɏ��ƁAK�n��
�̖ڐ����2m��1�C4m��2�ƂȂ�悤�Ɏ��ƁAK�n��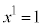 �������ʒu�́A
�������ʒu�́A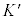 �n�ł�
�n�ł�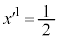 �ɂȂ�܂��B�ڐ���̎����ƍ��W�͔��̓��������܂��B�܂�A
�ɂȂ�܂��B�ڐ���̎����ƍ��W�͔��̓��������܂��B�܂�A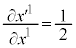 �ŁA���σx�N�g���̐���
�ŁA���σx�N�g���̐���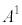 �́A
�́A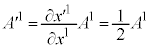 �ƁA�ڐ���̎����Ƃ͔��ɕϊ�����܂��B
�ƁA�ڐ���̎����Ƃ͔��ɕϊ�����܂��B
K�n�Ō��_��ʂ钼���̌X����1�̂Ƃ��A���̒����͓_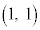 ��ʉ߂��܂��Bx���W��1���A
��ʉ߂��܂��Bx���W��1���A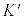 �n��
�n�� �ɂȂ�ƒ�����
�ɂȂ�ƒ�����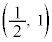 ��ʉ߂��܂��B
��ʉ߂��܂��B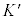 �n�ł́A�����̌X����2�ɂȂ�A�ڐ���̎����Ɠ������������܂��B�܂�A
�n�ł́A�����̌X����2�ɂȂ�A�ڐ���̎����Ɠ������������܂��B�܂�A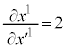 �ŁA���σx�N�g���̐����ł��钼���̌X��
�ŁA���σx�N�g���̐����ł��钼���̌X��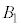 �́A
�́A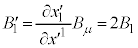 �ƁA�ڐ���̎����Ɠ����悤�ɕϊ�����܂��B
�ƁA�ڐ���̎����Ɠ����悤�ɕϊ�����܂��B
���σx�N�g���Ɠ��l�ɁA��t���Y����2�ɂȂ�A
�̂悤�ɕϊ�������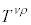 �����σe���\���ƌ����܂��B
�����σe���\���ƌ����܂��B
���σx�N�g���Ɠ��l�ɁA���t���Y����2�ɂȂ�A
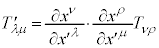 �@����@
�@����@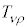 �����σe���\���ƌ����܂��B
�����σe���\���ƌ����܂��B
���ϐ����Ƌ��ϐ������������Ă��āA
�̂悤�ɕϊ�������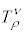 �������e���\���ƌ����܂��B
�������e���\���ƌ����܂��B
�������E�Ԋu��2��F
�Ƃ��Ē�`������v�ʃe���\��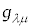 �͋��σe���\���ł��B�Ȃ��Ȃ�AK�n����
�͋��σe���\���ł��B�Ȃ��Ȃ�AK�n����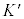 �n�ɕϊ������
�n�ɕϊ������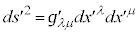 �ƂȂ�Ƃ��A���E�Ԋu��2��͕ω����Ȃ��̂ŁA
�ƂȂ�Ƃ��A���E�Ԋu��2��͕ω����Ȃ��̂ŁA
������A�v�ʃe���\��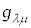 �́A
�́A
�Ƈ@�̂悤�ɕϊ������̂ŁA���σe���\���ł��B
���σx�N�g��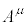 ���狤�σx�N�g��
���狤�σx�N�g��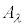 �����Ƃ��A�v�ʃe���\����p���āA
�����Ƃ��A�v�ʃe���\����p���āA
�Ƃ��܂��B�k�Ă���Y��μ��ν�ɓ���ւ���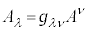 �̗��ӂɁA
�̗��ӂɁA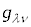 �̋t�s��
�̋t�s��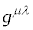 ��������ƁA
��������ƁA
�ƂȂ�A���̔��σx�N�g���ɖ߂�܂��B���l�ɋ��σx�N�g��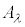 ���甽�σx�N�g��
���甽�σx�N�g��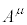 �����Ƃ��A
�����Ƃ��A
�Ƃ��܂��B���σe���\��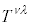 ���獬���e���\��
���獬���e���\��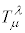 �����Ƃ��́A
�����Ƃ��́A
���σe���\��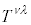 ���狤�σe���\��
���狤�σe���\��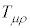 �����Ƃ��́A
�����Ƃ��́A
���σe���\��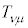 ���獬���e���\��
���獬���e���\��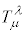 �����Ƃ��́A
�����Ƃ��́A
���σe���\��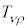 ���甽�σe���\��
���甽�σe���\��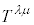 �����Ƃ��́A
�����Ƃ��́A
�Ƃ��܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@������b����TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 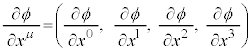 �́A�A���藝���A
�́A�A���藝���A