�v�ʃe���\��
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
������W�n�ɂ����āA�j���[�g���̉^���̑�1�@��(�����̖@��)�ɂ��ƁA�O�����������Ȃ����͓̂��������^���𑱂��܂��B�����������W�n�������n�ƌ����܂��B���銵���nK���猩�ē��������^�����镨�̂ɕt��������W�n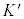 ���������n�ɂȂ�܂��B�����n���K�����C�n�Ƃ��A���W�n���K�����C�I�ł���A�Ƃ������܂��BK�n���猩��
���������n�ɂȂ�܂��B�����n���K�����C�n�Ƃ��A���W�n���K�����C�I�ł���A�Ƃ������܂��BK�n���猩��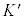 �n�����x���]��ɂ��傫���Ƃ��́A���W�ϊ��̓��[�����c�ϊ��ōl����K�v������܂��B
�n�����x���]��ɂ��傫���Ƃ��́A���W�ϊ��̓��[�����c�ϊ��ōl����K�v������܂��B
�A�C���V���^�C���̑��ΐ��̗v��(�����n�ɑ�����̂����ꑊ�ΐ��ƌ����܂�)�ɂ��ƁA�����@���́A�S�Ă̍��W�n�œ���̌`(���ςł���ƌ����܂�)�ɏ������K�v������܂��B�j���[�g���̉^��3�@���́A���[�����c�ϊ��ɑ��ċ��ςł͂���܂��A�}�N�X�E�F���̕������́A���[�����c�ϊ��ɑ��ċ��ςł��B���[�����c�ϊ��ł́A(�K�����C�I)��ԂƎ��ԂƂ��������Ă��܂��A�����čl���邱�Ƃ��ł��Ȃ��̂ŁA��ԂƎ��ԂƂ��܂Ƃ߂āA�~���R�t�X�L�[�����A�Ƃ����R�Ȏ���ƌ����܂��B��Ԃ����̏ꍇ�̓��[�N���b�h��Ԃƌ����܂��B
����ɑ��āA�����nK���猩�āA�����x�^�������Ă���n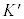 �����n�ƌ����܂��B���n�ɂ����Ă��A����������(������)�̓����ɂ���Ċ����n�Ƃ��Ĉ���(Newton�̉^��3�@���ʼn^�����l����)���Ƃ��ł��܂��B�A���A�����������n�ɂ���̂����n�ɂ���̂��f���邱�Ƃ͂ł��Ȃ��̂ł��B�������֎q�ɍ����ĕ��̂̉^���߂�Ƃ��A�����͊����n�ɂ���A�Ǝv���Ă��Ă��A�n���͎��]���Ă���̂ŁA�~�^��(�����x�^���ł�)�����Ă�����n�ł���n����ŕ��̂߂Ă���킯�ł��B�n�������z�̎���̌��]���Ă��邵�A���z�n����͌n�̒�����]�^�����Ă��邵�A�ǂ��Ɋ����n�����݂���̂��́A�������g�ł͂킩��܂���B�����ŁA�A�C���V���^�C���̑��ΐ��̗v���́A�����n�ł��낤���A���n�ł��낤���A�����@���͋��ςȌ`�ɕ\������˂Ȃ�Ȃ��A�Ƃ������ƂɂȂ�܂��B�������ʑ��ΐ��ƌ����܂��B
�����n�ƌ����܂��B���n�ɂ����Ă��A����������(������)�̓����ɂ���Ċ����n�Ƃ��Ĉ���(Newton�̉^��3�@���ʼn^�����l����)���Ƃ��ł��܂��B�A���A�����������n�ɂ���̂����n�ɂ���̂��f���邱�Ƃ͂ł��Ȃ��̂ł��B�������֎q�ɍ����ĕ��̂̉^���߂�Ƃ��A�����͊����n�ɂ���A�Ǝv���Ă��Ă��A�n���͎��]���Ă���̂ŁA�~�^��(�����x�^���ł�)�����Ă�����n�ł���n����ŕ��̂߂Ă���킯�ł��B�n�������z�̎���̌��]���Ă��邵�A���z�n����͌n�̒�����]�^�����Ă��邵�A�ǂ��Ɋ����n�����݂���̂��́A�������g�ł͂킩��܂���B�����ŁA�A�C���V���^�C���̑��ΐ��̗v���́A�����n�ł��낤���A���n�ł��낤���A�����@���͋��ςȌ`�ɕ\������˂Ȃ�Ȃ��A�Ƃ������ƂɂȂ�܂��B�������ʑ��ΐ��ƌ����܂��B
�����n�ɑ��������x�^�����Ă�����n�́A�����n�̃~���R�t�X�L�[����ɑ��āA���[�}������Ƃ��A�Ȃ�������Ԃƌ����܂��B�Ƃ���ŁA���n�ł́A��ʑ��ΐ������ł͕����w���\�z�ł��Ȃ��̂ŁA�A�C���V���^�C���́A�������̍l�����W�����āA������W�nK���d�������݂��Ă��AK�ɑ��������x�^��������W�n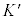 �����܂��ݒ肷����d���̌��ʂ���������
�����܂��ݒ肷����d���̌��ʂ���������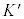 �������n�ɂł���A�Ƃ����l����(���������ƌ����܂�)�����āA��ʑ��ΐ����_�����܂����B����ɂ��ƁA������̂���1�_(���E�_�ƌ����܂�)�̎��͂ɋǏ��I�ɏd�͂������Ȃ��~���R�t�X�L�[����(���̌n���Ǐ������n�ƌ����܂�)��ݒ肵�āA���ꑊ�ΐ��Ɋ�Â������@�����\�z���A���̍��W�n�ɂ͈�ʍ��W�ϊ��ƌĂ����W�ϊ��Ŗ@����W�J���čs�����Ƃ��ł��܂��B
�������n�ɂł���A�Ƃ����l����(���������ƌ����܂�)�����āA��ʑ��ΐ����_�����܂����B����ɂ��ƁA������̂���1�_(���E�_�ƌ����܂�)�̎��͂ɋǏ��I�ɏd�͂������Ȃ��~���R�t�X�L�[����(���̌n���Ǐ������n�ƌ����܂�)��ݒ肵�āA���ꑊ�ΐ��Ɋ�Â������@�����\�z���A���̍��W�n�ɂ͈�ʍ��W�ϊ��ƌĂ����W�ϊ��Ŗ@����W�J���čs�����Ƃ��ł��܂��B
���[�}����Ԃł́A2�̐��E�_�̊Ԃ����������E�Ԋu�ƌ����܂��B�����ɗ��ꂽ2�̐��E�_�̊Ԃ̔������E�Ԋu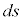 ��2����A�e���W���̔����ψ�
��2����A�e���W���̔����ψ�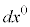 �C
�C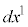 �C
�C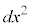 �C
�C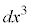 (�E��t���Y���͎w���ł͂���܂���B0�͎��ԁA1��x���W�A2��y���W�A3��z���W��\���Y���ł�)��p���āA
(�E��t���Y���͎w���ł͂���܂���B0�͎��ԁA1��x���W�A2��y���W�A3��z���W��\���Y���ł�)��p���āA
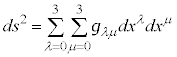 �@����@
�@����@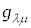 ���v�ʃe���\���ƌ����܂��B��ʓI�ɂ́A���W�n�̋Ȃ�����\���A���W
���v�ʃe���\���ƌ����܂��B��ʓI�ɂ́A���W�n�̋Ȃ�����\���A���W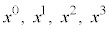 �̊��ł����Ē萔�ł͂���܂���B�A�C���V���^�C���͇@��Σ�����O���āA�@���A
�̊��ł����Ē萔�ł͂���܂���B�A�C���V���^�C���͇@��Σ�����O���āA�@���A
�Ə����܂����B��t���̓Y���Ɖ��t���̓Y���ɂ��āA��������λ�Cμ���o�Ă���ꍇ�ɂ́A �C
�C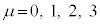 �Ƃ��ĉ������킹��A�Ɩ��܂����B������k���ƌ����܂��B
�Ƃ��ĉ������킹��A�Ɩ��܂����B������k���ƌ����܂��B
�������W�n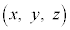 �ł́A
�ł́A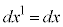 �C
�C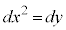 �C
�C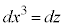 �Ƃ��āA�O�����̒藝���A
�Ƃ��āA�O�����̒藝���A
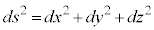 (
(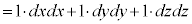 �C���̎���2�͎w����2�ł�)
�C���̎���2�͎w����2�ł�)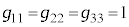 �C�v�ʃe���\���̑��̐�����0�ł��B
�C�v�ʃe���\���̑��̐�����0�ł��B
�~�����W�n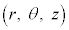 �ł́A
�ł́A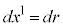 �C
�C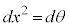 �C
�C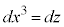 �Ƃ��āA
�Ƃ��āA
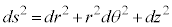 (
(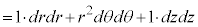 �C���̎���2���w����2�ł�)�@(���W�n���Q��)
�C���̎���2���w����2�ł�)�@(���W�n���Q��)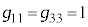 �C
�C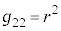 �C�v�ʃe���\���̑��̐�����0�ł��B
�C�v�ʃe���\���̑��̐�����0�ł��B
�����W�n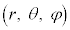 �ł́A
�ł́A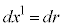 �C
�C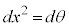 �C
�C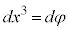 �Ƃ��āA
�Ƃ��āA
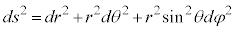 (
(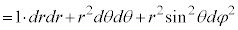 �C���̎���2���w����2�ł�)�@(���W�n���Q��)
�C���̎���2���w����2�ł�)�@(���W�n���Q��)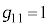 �C
�C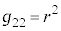 �C
�C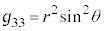 �C�v�ʃe���\���̑��̐�����0�ł��B
�C�v�ʃe���\���̑��̐�����0�ł��B
�~���R�t�X�L�[����ł́A��Ԃ�������2�悩������`�d������������ �ɑ�������������2��
�ɑ�������������2��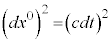 (c�F����)�������āA
(c�F����)�������āA
�ƂȂ�܂��B�E��̓Y������₱�����ł����A�J�b�R���̉E��̓Y���͎w���ł͂Ȃ��A�J�b�R�̊O�̉E��̐����͎w���ł��B���̏ꍇ�́A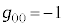 �C
�C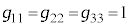 �C�v�ʃe���\���̑��̐�����0�ł��B�Ȃ��A
�C�v�ʃe���\���̑��̐�����0�ł��B�Ȃ��A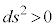 �Ƃ͌���܂���B
�Ƃ͌���܂���B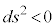 �̂Ƃ����E�Ԋu�͎��ԓI�A
�̂Ƃ����E�Ԋu�͎��ԓI�A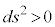 �̂Ƃ����E�Ԋu�͋�ԓI�A�ƌ����܂��B
�̂Ƃ����E�Ԋu�͋�ԓI�A�ƌ����܂��B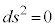 �̂Ƃ�
�̂Ƃ�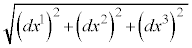 ����ԓI��������������
����ԓI��������������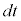 ����������c�Ői���Ƃ��Ӗ����܂��B
����������c�Ői���Ƃ��Ӗ����܂��B
�v�ʃe���\��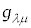 �́A���̒�`�@����Aλ�Cμ�̓���ւ��ł͒l��ς����A�s���ŕ\�������4���̐����s��ŁA10�̓Ɨ��Ȑ��������Ώ̍s��ł��B�܂��A
�́A���̒�`�@����Aλ�Cμ�̓���ւ��ł͒l��ς����A�s���ŕ\�������4���̐����s��ŁA10�̓Ɨ��Ȑ��������Ώ̍s��ł��B�܂��A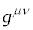 ��
��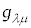 �̋t�s��ŁA
�̋t�s��ŁA
�ƂȂ�܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@������b����TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 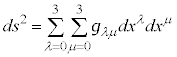 �@����@
�@����@