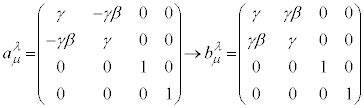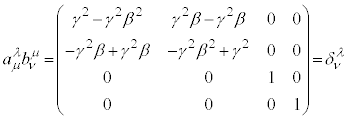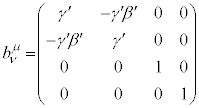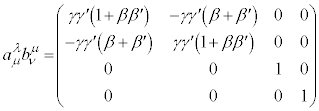���[�����c�ϊ�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
����Î~�nK�ɑ�������v�œ��������^��������W�n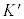 �ւ̍��W�ϊ����l���܂��B
�ւ̍��W�ϊ����l���܂��B
K�n�����Wx��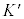 �n�����W
�n�����W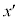 �ɕϊ������Ƃ��āA
�ɕϊ������Ƃ��āA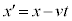 �ƂȂ�ϊ����K�����C�ϊ��ƌ����܂��B�j���[�g���̉^���������́A�K�����C�ϊ��ɑ��ċ��ςł��B�Ƃ��낪�A�}�N�X�E�F���̕������́A���̓K�����C�ϊ��ɑ��ċ��ςł͂���܂���BK�n�����x�ɐ���������(�������xB)�����݂���ꍇ�A
�ƂȂ�ϊ����K�����C�ϊ��ƌ����܂��B�j���[�g���̉^���������́A�K�����C�ϊ��ɑ��ċ��ςł��B�Ƃ��낪�A�}�N�X�E�F���̕������́A���̓K�����C�ϊ��ɑ��ċ��ςł͂���܂���BK�n�����x�ɐ���������(�������xB)�����݂���ꍇ�A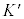 �n�ŐÎ~���Ă����d��q�ɂ��d���U���̖@���ɂ���N�d��
�n�ŐÎ~���Ă����d��q�ɂ��d���U���̖@���ɂ���N�d��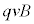 ����������͂��ł����A
����������͂��ł����A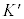 �n�ł��d�����Î~���Ă���̂ł����N�d���������܂���B�A�C���V���^�C���͍��Z���̍����炱�̓_�ɂ��ċ^��������Ă����Ƃ����`��������܂����A1905�N�̘_���ŁA
�n�ł��d�����Î~���Ă���̂ł����N�d���������܂���B�A�C���V���^�C���͍��Z���̍����炱�̓_�ɂ��ċ^��������Ă����Ƃ����`��������܂����A1905�N�̘_���ŁA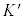 �n�ɂ��d��
�n�ɂ��d��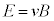 ����������A�ƌ��_���Ă��܂��B���ꂪ�A�A�C���V���^�C���̑��ΐ����_�̏o���_�ɂȂ��Ă��܂��B
����������A�ƌ��_���Ă��܂��B���ꂪ�A�A�C���V���^�C���̑��ΐ����_�̏o���_�ɂȂ��Ă��܂��B
�d�����d�������z���Ă��Ȃ��^��(�U�d��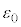 �C������
�C������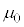 )�ł́A�}�N�X�E�F���̕��������g���������ƂȂ�A�`�d���x
)�ł́A�}�N�X�E�F���̕��������g���������ƂȂ�A�`�d���x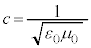 ���d���g��\���܂��B�`�d���x��������d���g��1��ł���ƍl�����܂����B19���I�ɂ́A�����`�d���x�͐�ΐÎ~�G�[�e���ɑ�����̂��ƍl�����Ă���A�n����̊ϑ��҂���ΐÎ~�G�[�e���ɑ��Ăǂ�قǂ����x�ňړ����Ă��邩�����o���悤�Ƃ����������s���܂������A1880�N��ɍs��ꂽ�}�C�P���\���E���[���[�̎����ɂ����Ă��A�������x�͌��o����܂���ł����B���[�����c�́A�ϑ��҂̈ړ������ɒ������k��(���[�����c���k�ƌ����܂�)�A�Ƃ��Ď������ʂ�������܂����B
���d���g��\���܂��B�`�d���x��������d���g��1��ł���ƍl�����܂����B19���I�ɂ́A�����`�d���x�͐�ΐÎ~�G�[�e���ɑ�����̂��ƍl�����Ă���A�n����̊ϑ��҂���ΐÎ~�G�[�e���ɑ��Ăǂ�قǂ����x�ňړ����Ă��邩�����o���悤�Ƃ����������s���܂������A1880�N��ɍs��ꂽ�}�C�P���\���E���[���[�̎����ɂ����Ă��A�������x�͌��o����܂���ł����B���[�����c�́A�ϑ��҂̈ړ������ɒ������k��(���[�����c���k�ƌ����܂�)�A�Ƃ��Ď������ʂ�������܂����B
����ɑ��āA�A�C���V���^�C���́A1905�N�̘_���ŁA�����@���͂��ׂĂ̊����n�œ������̂ł���A����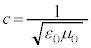 �͉^������ǂ̍��W�n�ɂ����Ă����ł���A�Ƃ��āA�K�����C�ϊ��ɑ���A�}�N�X�E�F���̕����������ςƂȂ���W�ϊ��̌����o���܂����B
�͉^������ǂ̍��W�n�ɂ����Ă����ł���A�Ƃ��āA�K�����C�ϊ��ɑ���A�}�N�X�E�F���̕����������ςƂȂ���W�ϊ��̌����o���܂����B
�����ŁA���銵���nK�ɑ��āAK�n��x��������������v�Ői�ފ����n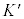 ���l���AK�ɂ�����x���W������t �ƁA
���l���AK�ɂ�����x���W������t �ƁA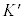 �ɂ�����x���W
�ɂ�����x���W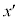 ������
������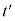 �Ƃ̊Ԃ̊W�ׂ܂��B
�Ƃ̊Ԃ̊W�ׂ܂��B
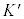 �n�ɂ�����x���ɐ����ȕ���������
�n�ɂ�����x���ɐ����ȕ���������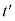 �̊ԂɌ�������h�i�ނƂ��A
�̊ԂɌ�������h�i�ނƂ��A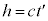 �ł��B�����K�n���猩��ƁA����t �̊ԂɁAx�������ɂ�����
�ł��B�����K�n���猩��ƁA����t �̊ԂɁAx�������ɂ�����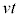 �����i�ނ悤�Ɍ�����̂Ō��̐i������
�����i�ނ悤�Ɍ�����̂Ō��̐i������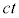 �ɂ��āA�O�����̒藝���A
�ɂ��āA�O�����̒藝���A
�@�́A�^�����Ă���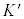 �n�ɂ����������́AK�n�ɂ��������������Z�����Ƃ��Ӗ����Ă��܂��B�u�^�����Ă��鎞�v�͒x���v�ƌ����܂��B
�n�ɂ����������́AK�n�ɂ��������������Z�����Ƃ��Ӗ����Ă��܂��B�u�^�����Ă��鎞�v�͒x���v�ƌ����܂��B
����0�ɁAK�n��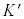 �n�̌��_����v���Ă��āA���_�Ō����_�����A
�n�̌��_����v���Ă��āA���_�Ō����_�����A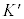 �n�ɂ����āA�ʒu
�n�ɂ����āA�ʒu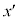 �ɒu���ꂽ���Ŕ��˂�������
�ɒu���ꂽ���Ŕ��˂�������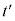 ��
��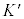 �̌��_
�̌��_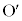 �ɖ߂��Ă����Ƃ��܂��B���̂Ƃ�
�ɖ߂��Ă����Ƃ��܂��B���̂Ƃ�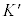 �n�Ō��āA���͉����^�����邾���Ȃ̂ŁA
�n�Ō��āA���͉����^�����邾���Ȃ̂ŁA
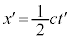 �@����A
�@����A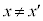 �ł��邱�Ƃɒ���)������
�ł��邱�Ƃɒ���)������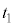 �̊Ԃ��ʒu
�̊Ԃ��ʒu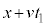 �ɗ����Ƃ��Ɍ������˂���Ƃ��āA
�ɗ����Ƃ��Ɍ������˂���Ƃ��āA
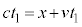 �@��
�@�� 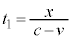
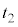 �̊ԂɁA�ʒu
�̊ԂɁA�ʒu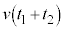 �܂ŗ��Ă���_
�܂ŗ��Ă���_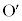 �ɖ߂�Ƃ��āA���̐i��������
�ɖ߂�Ƃ��āA���̐i��������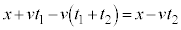 �Ȃ̂ŁA
�Ȃ̂ŁA
�����i�������ɂ��āAK�n��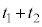 ��
��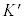 �n��
�n��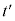 �ɑΉ�����̂ŁA�@���A
�ɑΉ�����̂ŁA�@���A
�A���A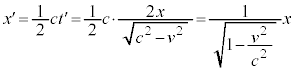 �@����B
�@����B
�B�́A�^�����Ă���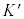 �n�ɂ���������
�n�ɂ���������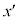 �́AK�n�Ō����
�́AK�n�Ō����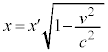 �ƂȂ�A�Z���ϑ�����邱�Ƃ��Ӗ����Ă��܂��B�������āA���[�����c���k����������܂��B
�ƂȂ�A�Z���ϑ�����邱�Ƃ��Ӗ����Ă��܂��B�������āA���[�����c���k����������܂��B
����0�ɂ����āA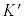 �n�̌��_
�n�̌��_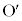 ��K�n�̌��_O�Ɉ�v���Ă����Ƃ��܂��B
��K�n�̌��_O�Ɉ�v���Ă����Ƃ��܂��B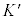 �n��K�n�ɑ���x������������v�ňړ����Ă����Ƃ���ƁA�_
�n��K�n�ɑ���x������������v�ňړ����Ă����Ƃ���ƁA�_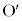 �́AK�n�ɂ����āA����t �ɂ������ʒu
�́AK�n�ɂ����āA����t �ɂ������ʒu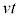 �ɂ���܂��B
�ɂ���܂��B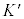 �n�ɂ��������W
�n�ɂ��������W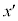 �́AK�n�ɂ�����
�́AK�n�ɂ�����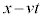 �ɑΉ����Ă���A���[�����c���k�̎��F�B���A
�ɑΉ����Ă���A���[�����c���k�̎��F�B���A
������A
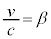 �C
�C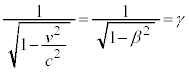 �@����C
�@����C
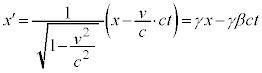 �@����D
�@����D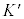 �n�Ƃ����ւ��Č���ƁA
�n�Ƃ����ւ��Č���ƁA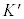 �n����K�n������v��x���������ɓ����Ă���̂ŁAx��
�n����K�n������v��x���������ɓ����Ă���̂ŁAx��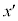 �����ւ���ƇD��
�����ւ���ƇD��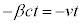 ��
��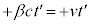 �ɕς��܂��B�����A
�ɕς��܂��B�����A
�D��������ƁA
K�n�ɑ�������v��x�������ɕ��i�^�����Ă���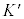 �ɂ�����4�����W
�ɂ�����4�����W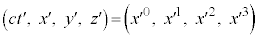 �́AK�n�����W
�́AK�n�����W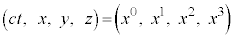 ��p���āA
��p���āA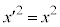 �C
�C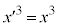 �Ƃ���(�Y���ׂ͂���̎w���ł͂Ȃ�4�����W�̂ǂꂩ�������ԍ��ł��B���σx�N�g���E���σx�N�g�����Q��)�A�s���p���ĕ\���ƁA
�Ƃ���(�Y���ׂ͂���̎w���ł͂Ȃ�4�����W�̂ǂꂩ�������ԍ��ł��B���σx�N�g���E���σx�N�g�����Q��)�A�s���p���ĕ\���ƁA
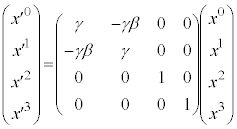 �@����E
�@����E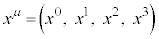 �C
�C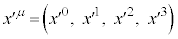 �Ə����ƁA����
�Ə����ƁA����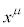 ����
����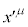 �ւ̕ϊ������[�����c�ϊ��ƌ����܂��B���[�����c�ϊ���\���s���
�ւ̕ϊ������[�����c�ϊ��ƌ����܂��B���[�����c�ϊ���\���s���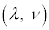 ����(
����(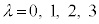 �C
�C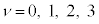 )��
)��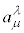 �Ə����ƁA
�Ə����ƁA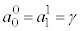 �C
�C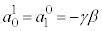 �C
�C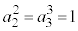 �C����
�C����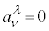 �ł��B���̂Ƃ��A���[�����c�ϊ��E���A
�ł��B���̂Ƃ��A���[�����c�ϊ��E���A
�ƕ\�����Ƃ��ł��܂��B
�~���R�t�X�L�[����(���R�Ȏ���)�ɂ��������E�Ԋus�́A
�Ƃ��Ē�`����܂�(�v�ʃe���\�����Q��)�B�~���R�t�X�L�[����ɂ�����v�ʃe���\���́A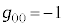 �C
�C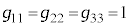 �C���̐�����0�Ȃ̂ŁA���[�����c�ϊ��F
�C���̐�����0�Ȃ̂ŁA���[�����c�ϊ��F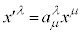 �C
�C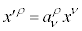 �ɂ��A
�ɂ��A
����āA���E�Ԋu��2��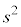 �́A���[�����c�ϊ��Ɋւ��ĕs�ςł��B�t�Ɍ����ƁA���E�Ԋu��2��
�́A���[�����c�ϊ��Ɋւ��ĕs�ςł��B�t�Ɍ����ƁA���E�Ԋu��2��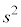 ��s�ςɂ���ϊ������[�����c�ϊ��ł��B�C��
��s�ςɂ���ϊ������[�����c�ϊ��ł��B�C��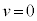 �̂Ƃ��A
�̂Ƃ��A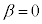 �C
�C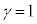 �ɂȂ�̂ŁA���[�����c�ϊ���\���s��
�ɂȂ�̂ŁA���[�����c�ϊ���\���s��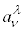 �͒P�ʍs��
�͒P�ʍs��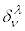 (
(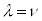 �̂Ƃ���1�C���̑���0�ƂȂ��e���\��)�ɂȂ�܂��B
�̂Ƃ���1�C���̑���0�ƂȂ��e���\��)�ɂȂ�܂��B
�܂��A�C��v ��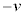 �Ƃ���ƁA
�Ƃ���ƁA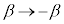 �C
�C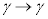 �ƂȂ�A
�ƂȂ�A
�ƂȂ�܂����A�C���A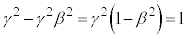 �Ȃ̂ŁA
�Ȃ̂ŁA
�܂�A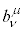 ��
��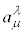 �̋t�s��ɂȂ��Ă��܂��B�܂��A
�̋t�s��ɂȂ��Ă��܂��B�܂��A
���Ƃ���ƁA
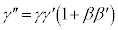 �C
�C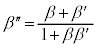 �Ƃ݂�A
�Ƃ݂�A
�Ə�����̂ŁA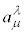 �Ɠ��l�̌`�����Ă��܂��B�܂�A���[�����c�ϊ�
�Ɠ��l�̌`�����Ă��܂��B�܂�A���[�����c�ϊ�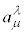 �̑S�̂́A�P�ʌ�
�̑S�̂́A�P�ʌ� �Ƌt���������A2�̌��̐ς��܂����[�����c�ϊ��ƂȂ�̂ŁA�Q���Ȃ��܂��B��������[�����c�Q�ƌ����܂��B
�Ƌt���������A2�̌��̐ς��܂����[�����c�ϊ��ƂȂ�̂ŁA�Q���Ȃ��܂��B��������[�����c�Q�ƌ����܂��B
���D���m�Ɍ����ƁA�E�̓��[�����c�E�u�[�X�g�ƌĂ�܂��B���m�ɂ́A�E�ɋ�ԓI�ȉ�]���{�������̂����[�����c�ϊ��ƌ����A���̕ϊ��S�̂Ń��[�����c�Q�����܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@������b����TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B  �@����@
�@����@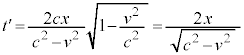
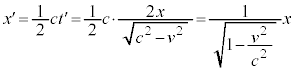 �@����B
�@����B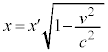 �ƂȂ�A�Z���ϑ�����邱�Ƃ��Ӗ����Ă��܂��B�������āA���[�����c���k����������܂��B
�ƂȂ�A�Z���ϑ�����邱�Ƃ��Ӗ����Ă��܂��B�������āA���[�����c���k����������܂��B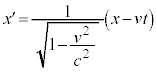
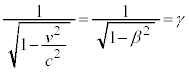 �@����C
�@����C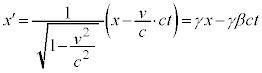 �@����D
�@����D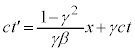 �C
�C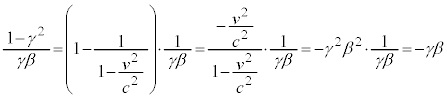
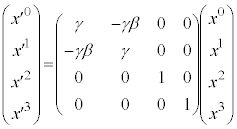 �@����E
�@����E