センター数学IA '06年第1問
[1] 2次方程式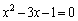
の解がα，β で、
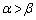とするとき、
，
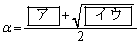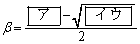
である。また、
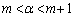を満たす整数mの値は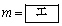
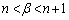を満たす整数nの値は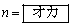
である。
次に、
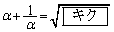
であり、
である。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 2次方程式の解の公式より、2次方程式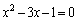
の解は、
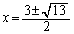
よって、[ア]は3，[イウ]は13
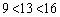より、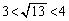
，
∴ 
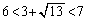
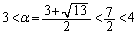
よって、[エ]は3
また、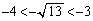
，
∴ 
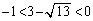
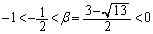
よって、[オカ]は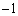
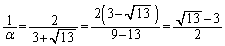(分母の有理化を参照)
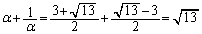
よって、[キク]は13
∴ 
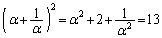
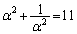
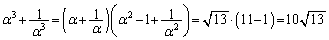
よって、[ケコ]は10，[サシ]は13
[別解]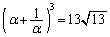 
，
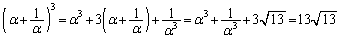より、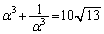
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[2] aは実数とし、bは0でない実数とする。aとbに関する条件p，q，rを次のように定める。
p： a，bはともに有理数である
q：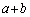 
，
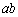はともに有理数である
r：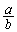 
は有理数である
(1) 次の
に当てはまるものを、下の
〜
のうちから一つ選べ。
条件pの否定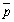
は
である。
「a，bはともに有理数である」
「a，bはともに無理数である」
「a，bの少なくとも一方は有理数である」
「a，bの少なくとも一方は無理数である」
(2) 次の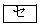
に当てはまるものを、下の〜のうちから一つ選べ。
条件「qかつr」は条件pが成り立つための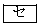
。
必要十分条件である
必要条件であるが十分条件ではない
十分条件であるが必要条件ではない
必要条件でも十分条件でもない
(3) 次の〜
のうち、正しいものは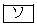
である。
「
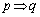」は真、「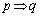
」の逆は真、「
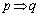」の対偶は真である。
「
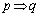」は真、「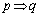
」の逆は真、「
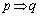」の対偶は偽である。
「
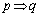」は真、「
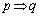」の逆は偽、「
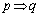」の対偶は真である。
「
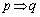」は真、「
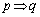」の逆は偽、「
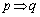」の対偶は偽である。
「
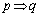」は偽、「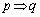
」の逆は真、「
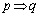」の対偶は真である。
「
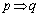」は偽、「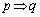
」の逆は真、「
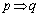」の対偶は偽である。
「
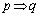」は偽、「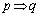
」の逆は偽、「
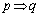」の対偶は真である。
「
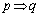」は偽、「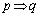
」の逆は偽、「
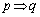」の対偶は偽である。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
(1) 「ともに云々」の否定は「どちらかは云々でない」なので、「ともに有理数」の否定は「どちらか一方は有理数でない」、つまり「どちらか一方は無理数」であって(条件・命題を参照)、[ス]は
(2) 「qかつr」⇒p の反例を見つけるのには、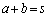
，
，
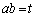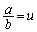(s，t，uは有理数)とおいて、a，bが無理数になる組み合わせを考えます。
a，bは、解と係数の関係より、2次方程式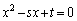
の2解で、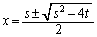
より、仮に、
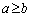だとして、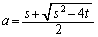
，
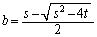
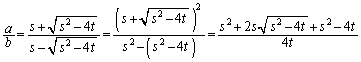
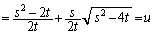
こうなるためには、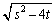
が有理数になるか、
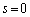であればよいのですが、
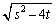が有理数だとすると、a，bも有理数になってしまうので、
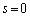とすればよいことがわかります。このとき、
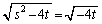が無理数、例えば、
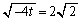とすると、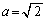
，
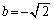となります。このとき、
，
，
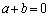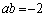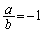はいずれも有理数ですが、a，bは無理数です。
よって、「qかつr」⇒p の反例は、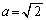
，
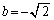であり、「qかつr」⇒pは偽です。
一方、a，bが有理数であれば、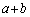
，
，
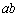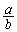はいずれも有理数であって、p⇒「qかつr」は、真です。
このとき、「qかつr」はpの必要条件であって十分条件ではありません。
よって、[セ]は、です。
試験会場では、ここまでていねいに考えると時間がなくなります。[1]がヒントになっていることをつかんで勘を働かせる必要があります。
(3) (2)で検討したように、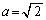
，
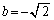のとき、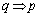
は成り立たないので、
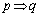の 逆 は偽です。
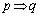は真です。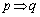
の対偶は、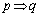
と同値なので、対偶も真です。
よって、[ソ]は、です。
センター試験の準備は、教科書の基礎事項をしっかりマスターし、ある程度、センター用の練習問題を解いたら、東京出版「センター試験必勝マニュアル 数学IA」(9月頃発売になります)を一通り読んでおきましょう。
数学TOP TOPページに戻る
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。