センター試験数学IA 2011年問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1][1] 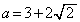 ,
,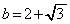 とすると
とすると
である。このとき、不等式
を満たすxの値の範囲は
となる。
[2] 実数a,bに関する条件p,qを次のように定める。
(1) 次の ~
~ のうち、命題「q ⇒ p」に対する反例になっているのは
のうち、命題「q ⇒ p」に対する反例になっているのは である。
である。 (2) 命題「p ⇒ q」の対偶は「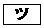 ⇒
⇒  」である。
」である。  ,
, に当てはまるものを、次の
に当てはまるものを、次の ~
~ のうちから一つずつ選べ。
のうちから一つずつ選べ。
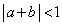 かつ
かつ 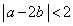

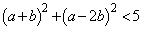

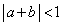 または
または 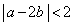

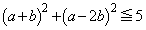

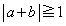 かつ
かつ 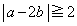

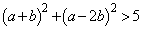

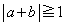 または
または 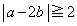

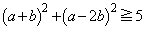
(3) pはqであるための 。
。  に当てはまるものを、次の
に当てはまるものを、次の ~
~ のうちから一つ選べ。
のうちから一つ選べ。 必要十分条件である
必要十分条件である 必要条件であるが、十分条件ではない
必要条件であるが、十分条件ではない 十分条件であるが、必要条件ではない
十分条件であるが、必要条件ではない 必要条件でも十分条件でもない
必要条件でも十分条件でもない
[2] a,b,cを定数とし、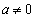 ,
,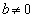 とする。xの2次関数
とする。xの2次関数
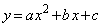 ・・・①
・・・①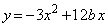 のグラフと同じ軸をもつとき
のグラフと同じ軸をもつとき
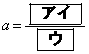 ・・・②
・・・②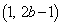 を通るとき
を通るとき
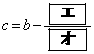 ・・・③
・・・③
以下、②,③のとき、2次関数①とそのグラフGを考える。
(1) Gとx軸が異なる2点で交わるようなbの値の範囲は
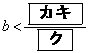 ,
,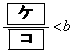
である。さらに、Gとx軸の正の部分が異なる2点で交わるようなbの値の範囲は
である。
(2) 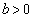 とする。
とする。 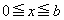 における2次関数①の最小値が
における2次関数①の最小値が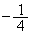 であるとき、
であるとき、
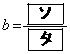 である。一方、
である。一方、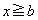 における2次関数①の最大値が3であるとき、
における2次関数①の最大値が3であるとき、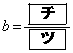 である。
である。
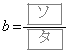 ,
,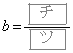 のときの①のグラフをそれぞれ
のときの①のグラフをそれぞれ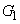 ,
,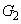 とする。
とする。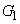 をx軸方向に
をx軸方向に ,y軸方向に
,y軸方向に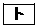 だけ平行移動すれば、
だけ平行移動すれば、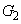 と一致する。
と一致する。
[3] 点Oを中心とする円Oの円周上に4点A,B,C,Dがこの順にある。四角形ABCDの辺の長さは、それぞれ
であるとする。
(1) 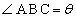 ,
,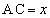 とおくと、△ABCに着目して
とおくと、△ABCに着目して となる。また、△ACDに着目して
となる。よって、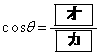 ,
,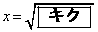 であり、円Oの半径は
であり、円Oの半径は である。
である。
また、四角形ABCDの面積は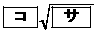 である。
である。
(2) 点Aにおける円Oの接線と点Dにおける円Oの接線の交点をEとすると、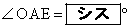 である。また、線分OEと辺ADの交点をFとすると、
である。また、線分OEと辺ADの交点をFとすると、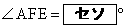 であり、
であり、 である。
さらに、辺ADの延長と線分OCの延長の交点をGとする。点Eから直線OGに垂線を下ろし、直線OGとの交点をHとする。4点E,G, は同一円周上にある。
は同一円周上にある。 に当てはまるものを次の
に当てはまるものを次の ~
~ から一つ選べ。
から一つ選べ。 C,F
C,F  H,D
H,D  H,F
H,F  H,A
H,A  O,Aしたがって
O,Aしたがって である。
[解答へ]
[4] 1個のさいころを投げるとき、4以下の目が出る確率pは であり、5以上の目が出る確率qは
であり、5以上の目が出る確率qは である。
である。
以下では、1個のさいころを8回繰り返して投げる。
(1) 8回の中で4以下の目がちょうど3回出る確率は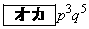 である。
である。 第1回目に4以下の目が出て、さらに次の7回の中で4以下の目がちょうど2回出る確率は である。
である。
第1回目に5以上の目が出て、さらに次の7回の中で4以下の目がちょうど3回出る確率は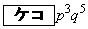 である。
である。
(2) 次の ~
~ のうち
のうち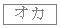 に等しいものは
に等しいものは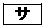 と
と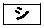 である。ただし、
である。ただし、 と
と は解答の順序を問わない。
は解答の順序を問わない。
(3) 得点を次のように定める。
8回の中で4以下の目がちょうど3回出た場合、
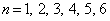 について、第n回目に初めて4以下の目が出たとき、得点はn点とする。
について、第n回目に初めて4以下の目が出たとき、得点はn点とする。また、4以下の目が出た回数がちょうど3回とならないときは、得点を0点とする。
このとき、得点が6点となる確率は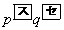 であり、得点が3点となる確率は
であり、得点が3点となる確率は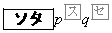 である。また、得点の期待値は
である。また、得点の期待値は である。
である。 [解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。  ・・・②
・・・② ・・・③
・・・③ ,
,
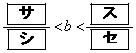
 である。一方、
である。一方、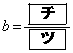 である。
である。 ,
, のときの①のグラフをそれぞれ
のときの①のグラフをそれぞれ ,
, であり、5以上の目が出る確率qは
であり、5以上の目が出る確率qは である。
である。 である。
である。