センター数学IA '11年第2問
a,b,cを定数とし、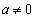 ,
,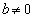 とする。xの2次関数
とする。xの2次関数
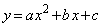 ・・・①
・・・①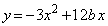 のグラフと同じ軸をもつとき
のグラフと同じ軸をもつとき
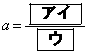 ・・・②
・・・②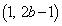 を通るとき
を通るとき
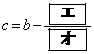 ・・・③
・・・③
以下、②,③のとき、2次関数①とそのグラフGを考える。
(1) Gとx軸が異なる2点で交わるようなbの値の範囲は
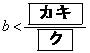 ,
,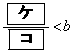
である。さらに、Gとx軸の正の部分が異なる2点で交わるようなbの値の範囲は
である。
(2) 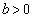 とする。
とする。 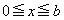 における2次関数①の最小値が
における2次関数①の最小値が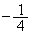 であるとき、
であるとき、
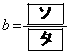 である。一方、
である。一方、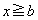 における2次関数①の最大値が3であるとき、
における2次関数①の最大値が3であるとき、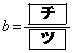 である。
である。
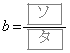 ,
,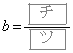 のときの①のグラフをそれぞれ
のときの①のグラフをそれぞれ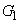 ,
,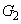 とする。
とする。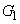 をx軸方向に
をx軸方向に ,y軸方向に
,y軸方向に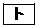 だけ平行移動すれば、
だけ平行移動すれば、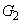 と一致する。
と一致する。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 計算がラクになるように配慮されていますが、センター試験としては、比較的高度な問題です。a,b,cの値、相互関係に注意して解答を進めます。
①右辺を平方完成して、
①のグラフGの軸は、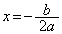 です。
です。
の軸は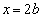 ですが、
ですが、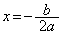 と一致するので、
と一致するので、
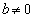 より、
より、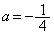
(ア) - (イ) 1 (ウ) 4 ......[答]
これで①は、
となりますが、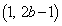 を通るので、
を通るので、
∴ 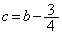
(エ) 3 (オ) 4 ......[答]
これも入れると、①は、
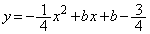 ・・・④
・・・④
(1) Gとx軸が異なる2点で交わるので、④で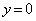 としてできる2次方程式、
としてできる2次方程式、 は、相異なる2実数解をもち、判別式Dについて、
∴ 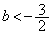 ,
,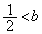 ・・・⑤(カ) - (キ) 3 (ク) 2 (ケ) 1 (コ) 2 ......[答]さらに、Gとx軸の正の部分が異なる2点で交わるので、⑤に付け加えて、
・・・⑤(カ) - (キ) 3 (ク) 2 (ケ) 1 (コ) 2 ......[答]さらに、Gとx軸の正の部分が異なる2点で交わるので、⑤に付け加えて、
④の軸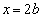 について、
について、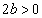 ・・・⑥ (2次方程式の解の配置を参照)
・・・⑥ (2次方程式の解の配置を参照)
Gのグラフが上に凸であることから、区間端(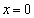 )において
)において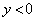 であって、
であって、 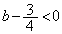 ・・・⑦
・・・⑦⑤ かつ ⑥ かつ ⑦より、
(サ) 1 (シ) 2 (ス) 3 (セ) 4 ......[答]
(2) Gの軸が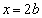 にあって、上に凸なので、
にあって、上に凸なので、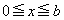 においては、2次関数①は単調増加です。④より、①は
においては、2次関数①は単調増加です。④より、①は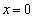 で最小値
で最小値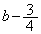 をとり、これが
をとり、これが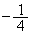 となることから、
となることから、 ∴ 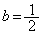
(ソ) 1 (タ) 2 ......[答]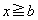 という範囲はGの軸の位置を含むので、④を平方完成して、
という範囲はGの軸の位置を含むので、④を平方完成して、 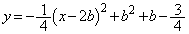 ・・・⑥
・・・⑥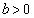 より、
より、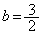 (チ) 3 (ツ) 2 ......[答]④で
(チ) 3 (ツ) 2 ......[答]④で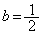 として、
として、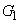 は、
は、⑥で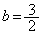 として、
として、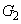 は、
は、 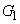 から
から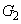 への平行移動は、頂点の移動で考えます。
への平行移動は、頂点の移動で考えます。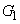 の頂点は
の頂点は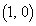 ,
,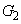 の頂点は
の頂点は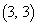 にあり、
にあり、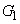 をx軸方向に2,y軸方向に3だけ平行移動すれば、
をx軸方向に2,y軸方向に3だけ平行移動すれば、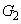 と一致します。(テ) 2 (ト) 3 ......[答]
と一致します。(テ) 2 (ト) 3 ......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。  ・・・②
・・・② ・・・③
・・・③ ,
,
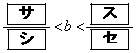
 である。一方、
である。一方、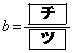 である。
である。 ,
, のときの①のグラフをそれぞれ
のときの①のグラフをそれぞれ