センター試験数学IA 2012年問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1][1](1) 不等式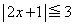 の解は
の解は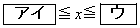 である。
である。 以下、aを自然数とする。
(2) 不等式
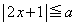 ・・・①
・・・①の解は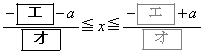 である。
である。 (3) 不等式①を満たす整数xの個数をNとする。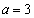 のとき、
のとき、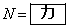 である。また、aが4,5,6,・・・と増加するとき、Nが初めて
である。また、aが4,5,6,・・・と増加するとき、Nが初めて より大きくなるのは、
より大きくなるのは、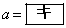 のときである。
のときである。
[2] kを定数とする。自然数m,nに関する条件p,q,rを次のように定める。
(1) 次の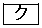 に当てはまるものを、下の
に当てはまるものを、下の ~
~ のうちから一つ選べ。
のうちから一つ選べ。 (2) 次の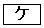 ~
~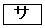 に当てはまるものを、下の
に当てはまるものを、下の ~
~ のうちから一つずつ選べ。ただし、同じものを繰り返し選んでもよい。
のうちから一つずつ選べ。ただし、同じものを繰り返し選んでもよい。 (i) 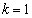 とする。
とする。 pはqであるための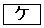 。
。 (ii) 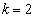 とする。
とする。 pはrであるための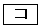 。pはqであるための
。pはqであるための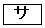 。
。  必要十分条件である
必要十分条件である
 必要条件であるが、十分条件でない
必要条件であるが、十分条件でない
 十分条件であるが、必要条件でない
十分条件であるが、必要条件でない
 必要条件でも十分条件でもない
必要条件でも十分条件でもない
[2] a,bを定数として2次関数
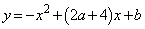 ・・・①
・・・①
である。以下、この頂点が直線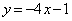 上にあるとする。このとき、
上にあるとする。このとき、
である。
(1) グラフGがx軸と異なる2点で交わるようなaの値の範囲は
である。また、Gがx軸の正の部分と負の部分の両方で交わるようなaの値の範囲は
である。
(2) 関数①の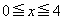 における最小値が
における最小値が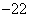 となるのは
となるのは  または
または 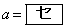
のときである。また、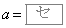 のとき、関数①の
のとき、関数①の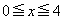 における最大値は
における最大値は である。
である。
一方、 のときの①のグラフをx軸方向に
のときの①のグラフをx軸方向に ,y軸方向に
,y軸方向に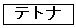 だけ平行移動すると、
だけ平行移動すると、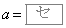 のときのグラフと一致する。
のときのグラフと一致する。 [解答へ]
[3] △ABCにおいて、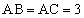 ,
,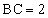 であるとき
であるとき
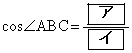 ,
,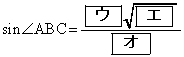
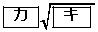 ,△ABCの内接円Iの半径は
,△ABCの内接円Iの半径は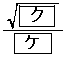 である。
である。
また、円Iの中心から点Bまでの距離は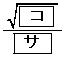 である。
である。
(1) 辺AB上の点Pと辺BC上の点Qを、BP=BQかつ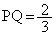 となるようにとる。このとき、△PBQの外接円Oの直径は
となるようにとる。このとき、△PBQの外接円Oの直径は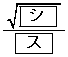 であり、円Iと円Oは
であり、円Iと円Oは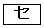 。ただし、
。ただし、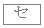 には次の
には次の ~
~ から当てはまるものを一つ選べ。
から当てはまるものを一つ選べ。  重なる(一致する)
重なる(一致する)  内接する
内接する  外接する
外接する 異なる2点で交わる
異なる2点で交わる  共有点をもたない
共有点をもたない
(2) 円I上に点Eと点Fを、3点C,E,Fが一直線上にこの順に並び、かつ、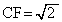 となるようにとる。このとき
となるようにとる。このとき 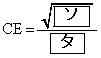 ,
,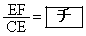
である。
さらに、円Iと辺BCとの接点をD,線分BEと線分DFとの交点をG,線分CGの延長と線分BFとの交点をMとする。このとき、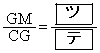 である。
である。 [解答へ]
[4] 1から9までの数字が一つずつ書かれた9枚のカードから5枚のカードを同時に取り出す。このようなカードの取り出し方は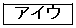 通りある。
通りある。
(1) 取り出した5枚のカードの中に5と書かれたカードがある取り出し方は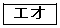 通りであり、5と書かれたカードがない取り出し方は
通りであり、5と書かれたカードがない取り出し方は 通りである。
通りである。
(2) 次のように得点を定める。
・取り出した5枚のカードの中に5と書かれたカードがない場合は、得点を0点とする。
・取り出した5枚のカードの中に5と書かれたカードがある場合、この5枚を書かれている数の小さい順に並べ、5と書かれたカードが小さい方からk番目にあるとき、得点をk点とする。
得点が0点となる確率は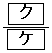 である。得点が1点となる確率は
である。得点が1点となる確率は で、得点が2点となる確率は
で、得点が2点となる確率は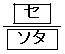 ,得点が3点となる確率は
,得点が3点となる確率は である。
である。
また、得点の期待値は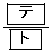 点である。
点である。 [解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 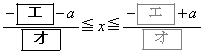 である。
である。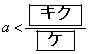
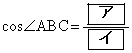 ,
,
 である。
である。 である。
である。 であり、円Iと円Oは
であり、円Iと円Oは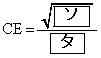 ,
,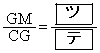 である。
である。 である。得点が1点となる確率は
である。得点が1点となる確率は で、得点が2点となる確率は
で、得点が2点となる確率は ,得点が3点となる確率は
,得点が3点となる確率は である。
である。 点である。
点である。