センター試験数学IA 2013年問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1][1] 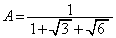 ,
,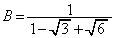 とする。
とする。 [2] 三角形に関する条件p,q,rを次のように定める。
p:三つの内角がすべて異なる。q:直角三角形でないr: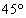 の内角は一つもない
の内角は一つもない
条件pの否定を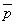 で表し、同様に
で表し、同様に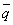 ,
,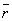 はそれぞれ条件q,rの否定を表すものとする。
はそれぞれ条件q,rの否定を表すものとする。 (1) 命題「r ⇒ (p または q)」の対偶は「 ⇒
⇒ 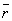 」である。
」である。  に当てはまるものを、次の
に当てはまるものを、次の ~
~ のうちから一つ選べ。
のうちから一つ選べ。
 (p かつ q)
(p かつ q)  (
(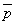 かつ
かつ 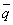 )
) (
(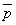 または q)
または q)  (
(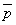 または
または 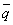 )
)(2) 次の ~
~ のうち、命題「(p または q) ⇒ r」に対する反例となっている三角形は
のうち、命題「(p または q) ⇒ r」に対する反例となっている三角形は と
と である。
である。  と
と に当てはまるものを、
に当てはまるものを、 ~
~ のうちから一つずつ選べ。ただし、
のうちから一つずつ選べ。ただし、 と
と の解答の順序は問わない。
の解答の順序は問わない。
 直角二等辺三角形
直角二等辺三角形
 内角が
内角が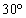 ,
,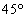 ,
,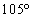 の三角形
の三角形
 正三角形
正三角形
 三辺の長さが3,4,5の三角形
三辺の長さが3,4,5の三角形
 頂角が
頂角が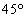 の二等辺三角形
の二等辺三角形(3) rは(p または q)であるための 。
。  に当てはまるものを、次の
に当てはまるものを、次の ~
~ のうちから一つ選べ。
のうちから一つ選べ。
 必要十分条件である
必要十分条件である
 必要条件であるが、十分条件ではない
必要条件であるが、十分条件ではない
 十分条件であるが、必要条件ではない
十分条件であるが、必要条件ではない
 必要条件でも十分条件でもない
必要条件でも十分条件でもない
[2] 座標平面上にある点Pは、点A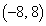 から出発して、直線
から出発して、直線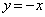 上をx座標が1秒あたり2増加するように一定の速さで動く。また、同じ座標平面上にある点Qは、点PがAを出発すると同時に原点Oから出発して、直線
上をx座標が1秒あたり2増加するように一定の速さで動く。また、同じ座標平面上にある点Qは、点PがAを出発すると同時に原点Oから出発して、直線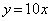 上をx座標が1秒あたり1増加するように一定の速さで動く。出発してからt秒後の2点P,Qを考える。点PがOに達するのは
上をx座標が1秒あたり1増加するように一定の速さで動く。出発してからt秒後の2点P,Qを考える。点PがOに達するのは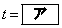 のときである。以下、
のときである。以下、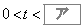 で考える。
で考える。 (1) 点Pとx座標が等しいx軸上の点を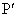 ,点Qとx座標が等しいx軸上の点を
,点Qとx座標が等しいx軸上の点を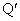 とおく。
とおく。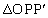 と
と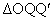 の面積の和Sをt で表せば
の面積の和Sをt で表せば となる。これより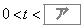 においては、
においては、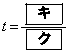 でSは最小値
でSは最小値 をとる。
をとる。
次に、aを を満たす定数とする。以下、
を満たす定数とする。以下、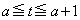 におけるSの最小・最大について考える。
におけるSの最小・最大について考える。 (i) Sが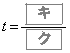 で最小となるようなaの値の範囲は
で最小となるようなaの値の範囲は 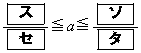 である。
である。(ii) Sが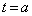 で最大となるようなaの値の範囲は
で最大となるようなaの値の範囲は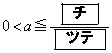 である。
である。 (2) 3点O,P,Qを通る2次関数のグラフが関数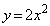 のグラフを平行移動したものになるのは、
のグラフを平行移動したものになるのは、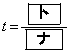 のときであり、x軸方向に
のときであり、x軸方向に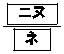 ,y軸方向に
,y軸方向に だけ平行移動すればよい。
だけ平行移動すればよい。 [解答へ]
[3] 点Oを中心とする半径3の円Oと、点Oを通り、点Pを中心とする半径1の円Pを考える。円Pの点Oにおける接線と円Oとの交点をA,Bとする。また、円Oの周上に、点Bと異なる点Cを、弦ACが円Pに接するようにとる。弦ACと円Pの接点をDとする。このとき
 ,
,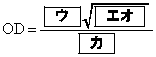
である。さらに、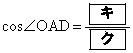 であり、
であり、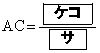 である。
である。
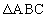 の面積は
の面積は であり、
であり、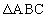 の内接円の半径は
の内接円の半径は である。
である。(1) 円Oの周上に、点Eを線分CEが円Oの直径となるようにとる。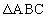 の内接円の中心をQとし、
の内接円の中心をQとし、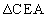 の内接円の中心をRとする。このとき、
の内接円の中心をRとする。このとき、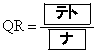 である。したがって、内接円Qと内接円Rは
である。したがって、内接円Qと内接円Rは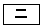 。
。  に当てはまるものを、次の
に当てはまるものを、次の ~
~ のうちから一つ選べ。
のうちから一つ選べ。
 内接する
内接する  異なる2点で交わる
異なる2点で交わる
 外接する
外接する  共有点を持たない
共有点を持たない(2) 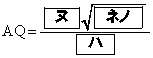 であるから、
であるから、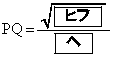 となる。
となる。 したがって、 。
。
 に当てはまるものを、次の
に当てはまるものを、次の ~
~ のうちから一つ選べ。
のうちから一つ選べ。
 点Pは内接円Qの周上にある
点Pは内接円Qの周上にある
 点Qは円Pの周上にある
点Qは円Pの周上にある
 点Pは内接円Qの内部にあり、点Qは円Pの内部にある
点Pは内接円Qの内部にあり、点Qは円Pの内部にある
 点Pは内接円Qの内部にあり、点Qは円Pの外部にある
点Pは内接円Qの内部にあり、点Qは円Pの外部にある [解答へ]
[4](1) 1から4までの数字を、重複を許して並べてできる4桁の自然数は、全部で 個ある。
個ある。 (2) (1)の 個の自然数のうちで、1から4までの数字を重複なく使ってできるものは
個の自然数のうちで、1から4までの数字を重複なく使ってできるものは 個ある。
個ある。 (3) (1)の 個の自然数のうちで、1331のように、異なる二つの数字を2回ずつ使ってできるものの個数を、次の考え方に従って求めよう。
個の自然数のうちで、1331のように、異なる二つの数字を2回ずつ使ってできるものの個数を、次の考え方に従って求めよう。 (i) 1から4までの数字から異なる二つを選ぶ。この選び方は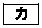 通りある。
通りある。 (ii) (i)で選んだ数字のうち小さい方を、一・十・百・千の位のうち、どの2箇所に置くか決める。置く2箇所の決め方は 通りある。小さい方の数字を置く場所を決めると、大きい方の数字を置く場所は残りの2箇所に決まる。
通りある。小さい方の数字を置く場所を決めると、大きい方の数字を置く場所は残りの2箇所に決まる。 (iii) (i)と(ii)により、求める個数は 個である。
個である。 (4) (1)の 個の自然数を、それぞれ別々のカードに書く。できた
個の自然数を、それぞれ別々のカードに書く。できた 枚のカードから1枚引き、それに書かれた数の四つの数字に応じて、得点を次のように定める。
枚のカードから1枚引き、それに書かれた数の四つの数字に応じて、得点を次のように定める。 ・四つとも同じ数字のとき 9点
・2回現れる数字が二つあるとき 3点
・3回現れる数字が一つと、
1回だけ現れる数字が一つあるとき 2点
・2回現れる数字が一つと、
1回だけ現れる数字が二つあるとき 1点
・数字の重複がないとき 0点
(i) 得点が9点となる確率は ,得点が3点となる確率は
,得点が3点となる確率は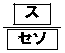 である。
である。 (ii) 得点が2点となる確率は ,得点が1点となる確率は
,得点が1点となる確率は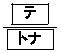 である。
である。 (iii) 得点の期待値は 点である。
点である。 [解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
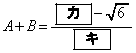
 でSは最小値
でSは最小値 をとる。
をとる。 で最小となるようなaの値の範囲は
で最小となるようなaの値の範囲は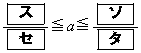 である。
である。 である。
である。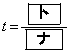 のときであり、x軸方向に
のときであり、x軸方向に ,y軸方向に
,y軸方向に だけ平行移動すればよい。
だけ平行移動すればよい。
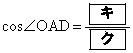 であり、
であり、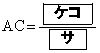 である。
である。 であり、
であり、 である。
である。 である。したがって、内接円Qと内接円Rは
である。したがって、内接円Qと内接円Rは であるから、
であるから、 となる。
となる。 ,得点が3点となる確率は
,得点が3点となる確率は である。
である。 ,得点が1点となる確率は
,得点が1点となる確率は である。
である。 点である。
点である。