大学入学共通テスト数学IA 2025年問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1][1] a,bを実数とする。xについての方程式
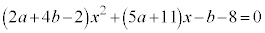 ・・・①
・・・①を考える。
(1) 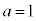 とする。
とする。 bに着目すると、①の左辺は
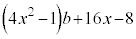 ・・・②
・・・②と表せる。よって、②を因数分解すると
となる。したがって、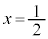 は①の解の一つであることがわかる。
は①の解の一つであることがわかる。
(2) 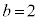 とする。
とする。 (i) ①の左辺を因数分解すると
となる。
(ii) 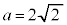 のとき、①の解は
のとき、①の解は となる。
(iii) 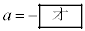 であることは、(1)の解が
であることは、(1)の解が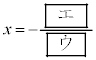 だけであるための
だけであるための 。
。  の解答群
の解答群 必要条件であるが、十分条件ではない
必要条件であるが、十分条件ではない
 十分条件であるが、必要条件ではない
十分条件であるが、必要条件ではない
 必要十分条件である
必要十分条件である
 必要条件でも十分条件でもない
必要条件でも十分条件でもない
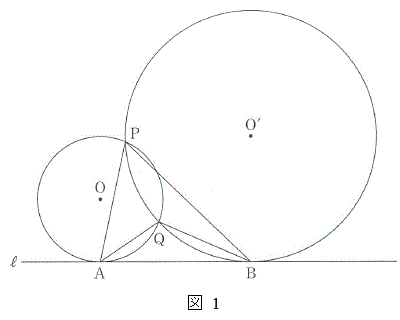 [2] 図1のように、直線
[2] 図1のように、直線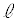 上の点Aにおいて
上の点Aにおいて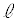 に接する半径2の円を円Oとし、
に接する半径2の円を円Oとし、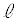 上の点Bにおいて
上の点Bにおいて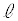 に接する半径4の円を円
に接する半径4の円を円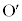 とする。円Oと円
とする。円Oと円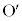 は2点で交わるとし、その交点をP,Qとする。ただし、
は2点で交わるとし、その交点をP,Qとする。ただし、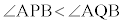 とする。さらに、
とする。さらに、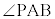 は鋭角であるとする。このとき、△PABと△QABについて考えよう。
は鋭角であるとする。このとき、△PABと△QABについて考えよう。
(1) 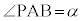 ,
,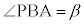 とおく。
とおく。 円Oの中心Oから直線PAに引いた垂線と直線PAとの交点をHとする。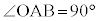 であるから、
であるから、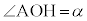 である。よって、△OAHに着目すると、
である。よって、△OAHに着目すると、 であるから
であるから 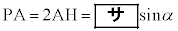 ・・・①
・・・①である。
同様にして、円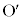 の中心
の中心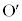 から直線PBに引いた垂線と直線PBとの交点を
から直線PBに引いた垂線と直線PBとの交点を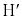 とすると
とすると 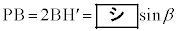 ・・・②
・・・②であることもわかる。
また、△PABの外接円の半径を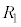 とおくと、正弦定理により
とおくと、正弦定理により が成り立つので
である。この式に①と②を代入することにより
となることがわかる。さらに
が得られる。
 ,
,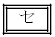 の解答群(同じものを繰り返し選んでもよい)
の解答群(同じものを繰り返し選んでもよい) α
α  β
β
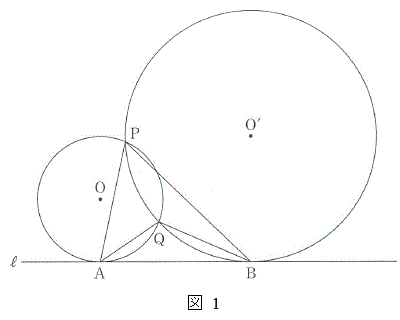 (2) 太郎さんと花子さんは、(1)の考察を振り返っている。
(2) 太郎さんと花子さんは、(1)の考察を振り返っている。
太郎:△QABの外接円の半径も求められるかな。
花子:(1)の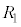 の求め方を参考にすればよさそうだね。
の求め方を参考にすればよさそうだね。 △PAB,△QABの外接円の半径をそれぞれ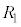 ,
,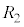 とおく。このとき、
とおく。このとき、 である。さらに、
である。さらに、 であることもわかる。
であることもわかる。  ,
, の解答群(同じものを繰り返し選んでもよい)
の解答群(同じものを繰り返し選んでもよい)
(3) 太郎さんと花子さんは、これまでの考察をもとに、△PABと△QABの辺の長さについて考えている。
太郎:ABの長さが与えられれば、PAとQAの長さが求められそうだね。
花子: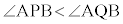 に注意して求めてみようよ。
に注意して求めてみようよ。 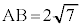 とする。このとき
とする。このときである。(1)より、 であるから
であるから である。
同様に、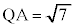 であることがわかる。
であることがわかる。
[解答へ]
 [2][1] [1] 花子さんと太郎さんは、公園にある二つの小さな噴水と大きな噴水の高さについて話している。
[2][1] [1] 花子さんと太郎さんは、公園にある二つの小さな噴水と大きな噴水の高さについて話している。
花子:あの中央の噴水の高さは何メートルだろう。
太郎:実際に高さを測定するのは難しそうだね。噴水の水がえがく曲線は、放物線になると聞いたことがあるよ。
花子:じゃあ、放物線と仮定して、およその高さを考えてみよう。
花子さんと太郎さんは、噴水の高さについて次のように考えることにした。
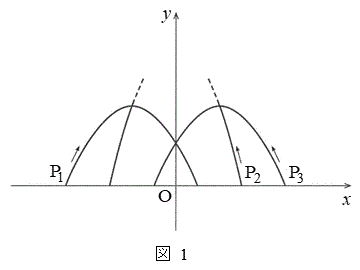 噴水のえがく曲線は三つとも放物線とする。三つの噴水の水が出る位置は水平な地面にある。図1のように座標軸が定められた平面上に、三つの噴水を正面から見た図をかく。左右の小さな噴水の水がえがく放物線については後の仮定1を、中央の大きな噴水の水がえがく放物線については後の仮定2を設定する。図1の
噴水のえがく曲線は三つとも放物線とする。三つの噴水の水が出る位置は水平な地面にある。図1のように座標軸が定められた平面上に、三つの噴水を正面から見た図をかく。左右の小さな噴水の水がえがく放物線については後の仮定1を、中央の大きな噴水の水がえがく放物線については後の仮定2を設定する。図1の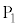 ,
,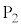 ,
,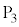 は噴水の水が出る位置である。なお、長さの単位はメートルであるが、以下では省略する。
は噴水の水が出る位置である。なお、長さの単位はメートルであるが、以下では省略する。
-仮定1----------------- ・左側の小さな噴水の水がえがく放物線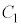 は、x軸上の点
は、x軸上の点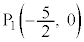 から出て点
から出て点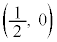 に至る。
に至る。 ・右側の小さな噴水の水がえがく放物線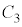 は、x軸上の点
は、x軸上の点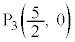 から出て点
から出て点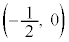 に至る。
に至る。 --------------------
-仮定2-----------------
中央の大きな噴水の水がえがく放物線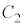 は、x軸上の点
は、x軸上の点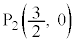 から出て
から出て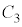 の頂点と
の頂点と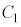 の頂点を通る。
の頂点を通る。
--------------------
(1) 仮定1と仮定2のもとで考える。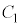 をグラフにもつ2次関数を
をグラフにもつ2次関数を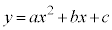 とする。このとき
とする。このとき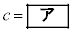 であり、また
であり、また である。
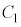 の頂点のy座標は
の頂点のy座標は である。このことを用いると、
である。このことを用いると、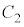 の頂点のy座標は
の頂点のy座標は であることがわかる。
であることがわかる。
したがって、大きな噴水の高さは、小さな噴水の高さの である。
である。
 については、最も適当なものを、次の
については、最も適当なものを、次の ~
~ のうちから一つ選べ。
のうちから一つ選べ。
(2) 花子さんと太郎さんは、大きな噴水の高さについて話している。
花子:正面から見たとき、大きな噴水が小さな噴水の頂点を通って見えるというデザインは変えずに、大きな噴水の高さを変えることはできるのかな。
太郎:左右の二つの小さな噴水は変えずに、大きな噴水の水が出る位置を変えてみたらどうかな。
花子:大きな噴水の高さが5メートルになるときの水が出る位置を考えてみよう。
仮定2の代わりに次の仮定2'をおく。
-仮定2'---------------
・中央の大きな噴水の水がえがく放物線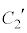 は、x軸の正の部分の点
は、x軸の正の部分の点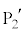 から出て
から出て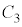 の頂点と
の頂点と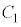 の頂点を通る。
の頂点を通る。 ・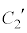 の頂点のy座標は5である。
の頂点のy座標は5である。 -------------------
仮定1と仮定2'のもとで考える。このとき、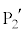 は
は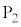 より
より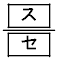 だけ
だけ の方にある。
の方にある。
 の解答群
の解答群
[2] 以下の問題を解答するにあたっては、与えられたデータに対して、次の値を外れ値とする。
------------------------
「(第1四分位数)-1.5×(四分位範囲)」以下の値
「(第3四分位数)+1.5×(四分位範囲)」以上の値
------------------------
太郎さんは、47都道府県における外国人宿泊者数と日本人宿泊者数の動向を調べるため、それらに関するデータを分析することにした。外国人宿泊者数を、日本国内に住所を有しない宿泊者数の人数の1年間の合計とし、日本人宿泊者数を、日本国内に住所を有する宿泊者の人数の1年間の合計とする。宿泊者数に関するデータは千の位を四捨五入し、1万人の単位で表したものとし、以下においては単位(万人)を省略して用いることとする。例えば、「4567890人」は「457」とする。
なお、以下の図や表については、国土交通省のWebページをもとに作成している。
(1)
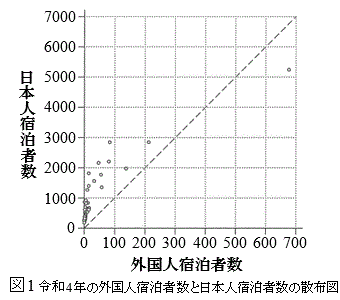 (i) 図1は、47都道府県における令和4年の外国人宿泊者数と日本人宿泊者数の散布図である。なお、散布図には原点を通り、傾きが10の直線(破線)を付加している。また、日本人宿泊者数が1000を超える都道府県の数は12である。
(i) 図1は、47都道府県における令和4年の外国人宿泊者数と日本人宿泊者数の散布図である。なお、散布図には原点を通り、傾きが10の直線(破線)を付加している。また、日本人宿泊者数が1000を超える都道府県の数は12である。
次の(a),(b)は、図1に関する記述である。
(a) 令和4年について、外国人宿泊者数が100を超え、かつ日本人宿泊者数が2500を超える都道府県の数は2である。
(b) 令和4年について、日本人宿泊者数が外国人宿泊者数の10倍未満である都道府県の割合は50%未満である。
(a),(b)の正誤の組み合わせとして正しいものは である。
である。
 の解答群
の解答群
(ii) 47都道府県における令和4年の外国人宿泊者数を分析した結果、外れ値となる都道府県の数は8であった。
一方、表1は47都道府県における令和4年の日本人宿泊者数を、値の小さい順に並べ、その順に都道府県P1,P2,・・・,P47としたものである。この中で、外国人宿泊者数で外れ値となる都道府県(P37,P40,P42,P43,P44,P45,P46,P47)に印*を付けている。
表1 47都道府県における令和4年の日本人宿泊者数
| 都道府県 | 日本人宿泊者数 |
| 都道府県 | 日本人宿泊者数 |
| 都道府県 | 日本人宿泊者数 |
| 都道府県 | 日本人宿泊者数 |
| P1 | 182 |
| P13 | 373 |
| P25 | 620 |
| P37* | 1339 |
| P2 | 187 |
| P14 | 388 |
| P26 | 625 |
| P38 | 1399 |
| P3 | 197 |
| P15 | 395 |
| P27 | 646 |
| P39 | 1547 |
| P4 | 204 |
| P16 | 401 |
| P28 | 670 |
| P40* | 1765 |
| P5 | 255 |
| P17 | 405 |
| P29 | 683 |
| P41 | 1814 |
| P6 | 270 |
| P18 | 452 |
| P30 | 705 |
| P42* | 1970 |
| P7 | 276 |
| P19 | 458 |
| P31 | 831 |
| P43* | 2158 |
| P8 | 286 |
| P20 | 501 |
| P32 | 832 |
| P44* | 2195 |
| P9 | 303 |
| P21 | 522 |
| P33 | 839 |
| P45* | 2831 |
| P10 | 321 |
| P22 | 537 |
| P34 | 876 |
| P46* | 2839 |
| P11 | 328 |
| P23 | 605 |
| P35 | 925 |
| P47* | 5226 |
| P12 | 351 |
| P24 | 613 |
| P36 | 1251 |
| | |
表1のデータにおいて、四分位範囲は となることから、令和4年の外国人宿泊者数と日本人宿泊者数の両方で外れ値となる都道府県の数は
となることから、令和4年の外国人宿泊者数と日本人宿泊者数の両方で外れ値となる都道府県の数は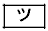 である。
である。
 の解答群
の解答群  320
320  450
450  597
597  638
638  900
900  966
966  1253
1253  1261
1261 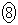 1603
1603 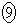 1864
1864
(2) 47都道府県におけるある都市の外国人宿泊者数をx,日本人宿泊者数をyとし、xとyの値の組を、それぞれ
と表す。x,yの平均値をそれぞれ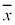 ,
,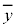 とし、x,yの分散をそれぞれ
とし、x,yの分散をそれぞれ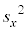 ,
,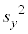 とする。また、xとyの共分散を
とする。また、xとyの共分散を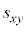 とする。47都道府県それぞれにおける外国人宿泊者数と日本人宿泊者数を足し合わせた合計宿泊者数をzとし、その値を
とする。47都道府県それぞれにおける外国人宿泊者数と日本人宿泊者数を足し合わせた合計宿泊者数をzとし、その値を 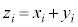 (
(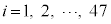 )
)と表す。例えば、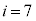 のときは
のときは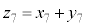 である。zの平均値を
である。zの平均値を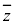 とするとき
とするとき である。このことに着目すると、zの分散を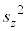 とするとき、
とするとき、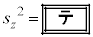 となる。
となる。
 また、令和4年のxとyの間には正の相関があることが図1からわかる。このことから、令和4年について、
また、令和4年のxとyの間には正の相関があることが図1からわかる。このことから、令和4年について、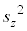 と
と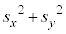 の関係として、後の
の関係として、後の ~
~ のうち、正しいものは
のうち、正しいものは であることがわかる。
であることがわかる。
 の解答群
の解答群  の解答群
の解答群
(3) 太郎さんが住む地域では、その地域に宿泊を促すためのキャンペーンとして、キャンペーンA,Bが実施されている。
太郎さんは、キャンペーンAの方がよいと思っている人が多いといううわさを聞いた。このうわさのとおり、キャンペーンAの方がよいと思っている人が多いといえるかどうか確かめることにした。そこで、かたよりなく選んだ人たちに、キャンペーンA,Bののどちらがよいかについて、二択のアンケートを行ったところ、アンケートに回答した35人のうち、23人が「キャンペーンAの方がよい」と答えた。この結果から、一般にキャンペーンAの方がよいとと思っている人が多いといえるかどうかを、次の方針で考えることにした。
-方針-----------------
・"「キャンペーンAの方がよい」と回答する割合と「キャンペーンBの方がよい」と回答する割合は等しい"という仮説を立てる。
・この仮説のもとで、かたよりなく選ばれた35人のうち23人以上が「キャンペーンAの方がよい」と回答する確率が5%未満であれば、その仮説は誤っていると判断し、5%以上であればその仮説は誤っているとは判断しない。
--------------------
後の実験結果は、35枚の硬貨を投げる実験を1000回行ったとき、表が出た枚数ごとの回数の割合を示したものである。実験結果 | 表の枚数(枚) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 割合(%) | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.1 | 0.1 | 0.8 | 1.3 |
| 表の枚数(枚) | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 割合(%) | 2.2 | 4.5 | 6.9 | 9.5 | 12.3 | 13.0 | 12.9 | 11.2 | 9.6 | 7.2 | 4.1 | 2.4 |
| 表の枚数(枚) | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 |
| 割合(%) | 0.9 | 0.5 | 0.4 | 0.0 | 0.1 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
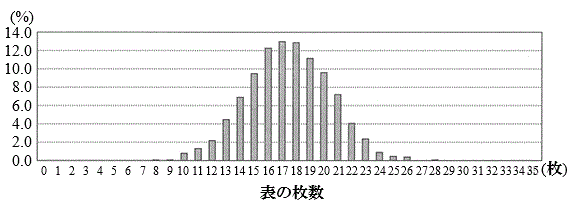 実験結果を用いると、35枚の硬貨のうち23枚以上が表となった割合は、
実験結果を用いると、35枚の硬貨のうち23枚以上が表となった割合は、 %である。これを、35人のうち23人以上が「キャンペーンAの方がよい」と回答する確率とみなし、方針に従うと、"「キャンペーンAの方がよい」と回答する割合と「キャンペーンBの方がよい」と回答する割合は等しい"という仮説は
%である。これを、35人のうち23人以上が「キャンペーンAの方がよい」と回答する確率とみなし、方針に従うと、"「キャンペーンAの方がよい」と回答する割合と「キャンペーンBの方がよい」と回答する割合は等しい"という仮説は 。したがって、今回のアンケート結果からは、キャンペーンAの方がよいと思っている人が
。したがって、今回のアンケート結果からは、キャンペーンAの方がよいと思っている人が 。
。
 ,
, については、最も適当なものを、次のそれぞれの解答群から一つずつ選べ。
については、最も適当なものを、次のそれぞれの解答群から一つずつ選べ。
 の解答群
の解答群  誤っていると判断する
誤っていると判断する
 誤っているとは判断しない
誤っているとは判断しない の解答群
の解答群 多いといえる
多いといえる
 多いとはいえない
多いとはいえない
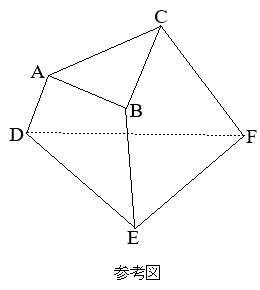 [3] 6点A,B,C,D,E,Fを頂点とし、三角形ABCとDEF,および四角形ABED,ACFD,BCFEを面とする五面体がある。ただし、直線ADとBEは平行でないとする。
[3] 6点A,B,C,D,E,Fを頂点とし、三角形ABCとDEF,および四角形ABED,ACFD,BCFEを面とする五面体がある。ただし、直線ADとBEは平行でないとする。
以下では、例えば、面ABCを含む平面を平面ABC,面ABEDを含む平面を平面ABED,などということにする。
(1) 3直線AD,BE,CFは1点で交わる。これを証明しよう。
直線ADとBEは平面ABED上にあり、平行でないので1点で交わる。その交点をPとする。
点Pは直線AD上にあり、直線ADは平面ABEDと平面 との交線であるから、点Pは平面
との交線であるから、点Pは平面 上にあることがわかる。
上にあることがわかる。
また、点Pは直線BE上にあり、直線BEは平面ABEDと平面 との交線であるから、点Pは平面
との交線であるから、点Pは平面 上にあることがわかる。
上にあることがわかる。
平面 と平面
と平面 との交線は直線CFであるから、点Pは直線CF上にもあることがわかる。したがって、3直線AD,BE,CFは点Pで交わる。
との交線は直線CFであるから、点Pは直線CF上にもあることがわかる。したがって、3直線AD,BE,CFは点Pで交わる。
 ,
, の解答群(同じものを繰り返し選んでもよい)
の解答群(同じものを繰り返し選んでもよい)
(2) 五面体において、面ABCは一辺の長さが3の正三角形であり
であるとする。また、6点A,B,C,D,E,Fはある1つの球面上にあるとし、その球面をSとする。直線ADとBEの交点をPとする。
(i) 平面ABEDと球面Sが交わる部分は円であり、4点A,B,E,Dはその円周上にある。このことから、三角形PABとPEDは相似であることがわかり、その相似比は1: である。したがって
である。したがって が成り立つ。よって
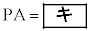 ,
,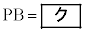
となる。
(ii) 平面BCFEと球面Sが交わる部分に着目すると、方べきの定理より
となる。したがって
 ,
,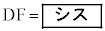
となる。
(iii) 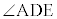 ,
,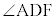 ,
,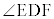 の大きさに着目すると、次の命題(a),(b),(c)の真偽の組み合わせとして正しいものは
の大きさに着目すると、次の命題(a),(b),(c)の真偽の組み合わせとして正しいものは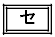 であることがわかる。
であることがわかる。
(a) 平面ABEDと平面DEFは垂直である。
(b) 直線DEは平面ACFDに垂直である。
(c) 直線ACと直線DEは垂直である。
 の解答群
の解答群
| |  |  |  |  |  |  |  |  |
| (a) | 真 | 真 | 真 | 真 | 偽 | 偽 | 偽 | 偽 |
| (b) | 真 | 真 | 偽 | 偽 | 真 | 真 | 偽 | 偽 |
| (c) | 真 | 偽 | 真 | 偽 | 真 | 偽 | 真 | 偽 |
[4] ある行事で、主催者が次のゲームを企画している。
-ゲーム----------------
参加者はくじを最大3回引き、当たりが出たら、1200円相当の景品を主催者から受け取り、以降はくじを引かない。参加者はくじを1回目、2回目、3回目で異なる箱から引く。1回目のくじ引きであたりが出なかった場合は2回目のくじを引き、2回目のくじ引きでもあたりが出なかった場合は3回目のくじを引く。主催者は、当たりの出る確率について次のとおり設定する。
・1回目に当たりが出る確率は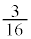 である。
である。
・1回目に当たりが出ず、かつ2回目に当たりが出る確率は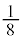 である。
である。 ・1回目、2回目ともに当たりが出ず、かつ3回目に当たりが出る確率は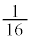 である。
である。 --------------------
ゲームの参加料について、主催者は2種類の支払い方法を考えている。参加料に関する設定の妥当性について、主催者は判断を行う。
(1) 1回目または2回目に当たりが出る確率は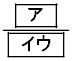 である。このことから、1回目、2回目ともに当たりが出ない確率は
である。このことから、1回目、2回目ともに当たりが出ない確率は であることがわかる。1回もあたりが出ない確率は
であることがわかる。1回もあたりが出ない確率は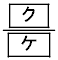 である。
である。
以下では、主催者が参加者に対して負担する金額をX円とする。すなわち、参加者がゲームで景品を受け取るとき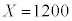 ,参加者がゲームで景品を受け取らないとき
,参加者がゲームで景品を受け取らないとき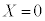 である。
である。
(2)
(i) 数量Xの期待値は である。なお、必要に応じて、次に示す表を用いて考えてもよい。
である。なお、必要に応じて、次に示す表を用いて考えてもよい。
(ii) 次の支払方法1を考える。
-支払方法1--------------
参加者は1回目のくじを引く直前に参加料500円を支払う。
--------------------支払方法1の場合、主催者が負担する金額X円の期待値が、参加料の金額500円未満であるとき、主催者の設定は妥当であると判断し、参加料の金額500円以上であるとき、参加料の設定は妥当ではないと判断する。(i)で求めたX円の期待値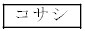 円は参加料の金額500円
円は参加料の金額500円 。したがって、主催者は参加料500円という設定について
。したがって、主催者は参加料500円という設定について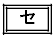 と判断する。
と判断する。
 の解答群
の解答群
 未満である
未満である  以上である
以上である
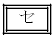 の解答群
の解答群
 妥当である
妥当である  妥当ではない
妥当ではない
(3) aを正の整数とする。次の支払方法2を考える。
-支払方法2--------------
参加者は1回目、2回目、3回目のくじを引く直前にそれぞれ料金a円を支払う。なお、この料金をくじ引き料といい、当たりが出た後は、くじを引かないため、くじ引き料を支払わないことになる。
--------------------
次の支払方法2で、ゲームを通して参加者が支払うくじ引き料の合計を参加料とし、Y円で表す。
(i) 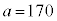 とする。このとき、次が成り立つ。
とする。このとき、次が成り立つ。 ・1回目に当たりが出るとき、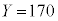 である。
である。 ・1回目に当たりが出ず、かつ2回目に当たりが出るとき、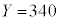 である。
である。 ・1回目、2回目ともに当たりが出ないとき、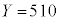 である。
である。 数量Yの期待値は である。なお、必要に応じて、次に示す表を用いて考えてもよい。
である。なお、必要に応じて、次に示す表を用いて考えてもよい。
(ii) 支払方法2の場合、主催者が負担する金額X円の期待値が、参加料Y円の期待値未満であるとき、主催者はくじ引き料の設定は妥当であると判断し、参加料Y円の期待値以上であるとき、くじ引き料の設定は妥当ではないと判断する。
(2)の(i)で求めたX円の期待値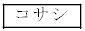 円は、
円は、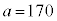 と設定した場合の支払方法2で参加者が支払う参加料Y円の期待値
と設定した場合の支払方法2で参加者が支払う参加料Y円の期待値 円
円 。したがって、主催者はくじ引き料170円という設定について
。したがって、主催者はくじ引き料170円という設定について と判断する。
と判断する。
また、主催者がくじ引き料の設定が妥当であると判断するのは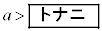 のときであり、主催者がくじ引き料の設定が妥当ではないと判断するのは
のときであり、主催者がくじ引き料の設定が妥当ではないと判断するのは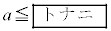 のときである。
のときである。
 の解答群
の解答群
 未満である
未満である  以上である
以上である
 の解答群
の解答群
 妥当である
妥当である  妥当ではない
妥当ではない
[解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2025(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
 だけであるための
だけであるための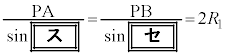
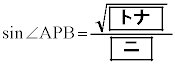
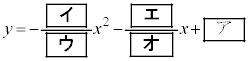
 である。このことを用いると、
である。このことを用いると、 であることがわかる。
であることがわかる。 だけ
だけ である。このことから、1回目、2回目ともに当たりが出ない確率は
である。このことから、1回目、2回目ともに当たりが出ない確率は であることがわかる。1回もあたりが出ない確率は
であることがわかる。1回もあたりが出ない確率は である。
である。