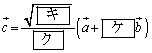センター試験数学IIB 2006年問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1][1] 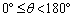 の範囲で関数
の範囲で関数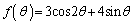 を考える。
を考える。
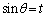 とおけば
とおけば
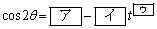
であるから、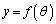 とおくと
とおくと
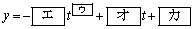
である。したがって、yの最大値は であり、最小値は
であり、最小値は である。
である。
また、αが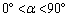 を満たす角度で
を満たす角度で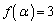 のとき
のとき
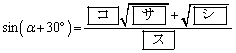
である。
[2] 不等式
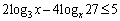 ・・・・・・(*)
・・・・・・(*)
が成り立つようなxの値の範囲を求めよう。
(1) 不等式(*)において、xは対数の底であるから
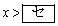 かつ
かつ 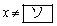
を満たさなければならない。また
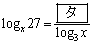
である。
(2) 不等式(*)は
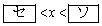 のとき
のとき

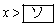 のとき
のとき

と変形できる。したがって、求めるxの値の範囲は
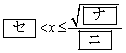 ,
,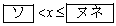
である。
[解答へ]
[2] aを正の実数として、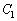 ,
,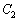 をそれぞれ次の2次関数のグラフとする。
をそれぞれ次の2次関数のグラフとする。
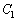 :
: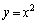
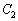 :
: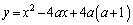
また、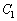 と
と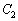 の両方に接する直線をlとする。
の両方に接する直線をlとする。
(1) 点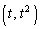 における
における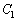 の接線の方程式は
の接線の方程式は
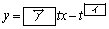
であり、この直線が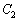 に接するのは
に接するのは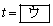 のときである。
のときである。
したがって、直線lの方程式は
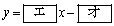
であり、lと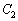 の接点の座標は
の接点の座標は

である。
(2) 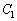 と
と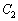 の交点をPとすると、Pの座標は
の交点をPとすると、Pの座標は
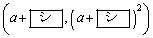
である。点Pを通って直線lに平行な直線をmとする。直線mの方程式は
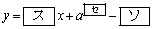
である。直線mとy軸との交点のy座標が正となるようなaの値の範囲は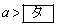 である。
である。
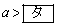 のとき、
のとき、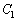 の
の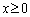 の部分と直線mおよびy軸で囲まれた図形の面積Sはaを用いて
の部分と直線mおよびy軸で囲まれた図形の面積Sはaを用いて
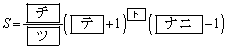
と表される。
[解答へ]
[3] a,b,cを相異なる実数とする。数列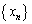 は等差数列で、最初の3項が順にa,b,cであるとし、数列
は等差数列で、最初の3項が順にa,b,cであるとし、数列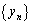 は等比数列で、最初の3項が順にc,a,bであるとする。
は等比数列で、最初の3項が順にc,a,bであるとする。
(1) bとcはaを用いて
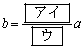 ,
,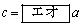
と表され、等差数列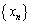 の公差は
の公差は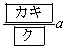 である。
である。
(2) 等比数列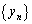 の公比は
の公比は であるから、
であるから、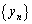 の初項から第8項までの和は、aを用いて
の初項から第8項までの和は、aを用いて

と表される。
(3) 数列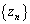 は最初の3項が順にb,c,aであり、その階差数列
は最初の3項が順にb,c,aであり、その階差数列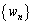 が等差数列であるとする。このとき、
が等差数列であるとする。このとき、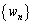 の公差は
の公差は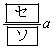 であり、
であり、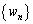 の一般項は
の一般項は
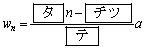
である。したがって、数列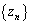 の一般項は、aを用いて
の一般項は、aを用いて
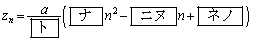
と表される。
[解答へ]
[4] 平面上の三つのベクトル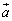 ,
,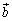 ,
,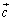 は
は
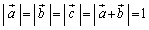
を満たし、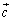 は
は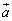 に垂直で、
に垂直で、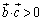 であるとする。
であるとする。
(1) 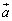 と
と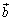 の内積は
の内積は
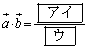
である。また
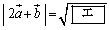
であり、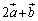 と
と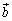 のなす角は
のなす角は である。
である。
(2) ベクトル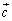 を
を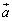 と
と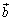 で表すと
で表すと
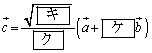
である。
(3) x,yを実数とする。ベクトル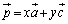 が
が
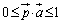 ,
,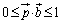
を満たすための必要十分条件は
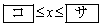 ,
,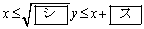
である。xとyが上の範囲を動くとき、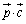 は最大値
は最大値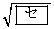 をとり、この最大値をとるときの
をとり、この最大値をとるときの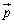 を
を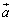 と
と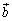 で表すと
で表すと
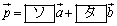
である。
[解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
 ,
,