センター試験数学IIB 2007年問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1][1] 不等式
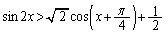
を満たすxの範囲を求めよう。ただし、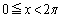 とする。
とする。
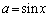 ,
,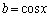 とおくと、与えられた不等式は
とおくと、与えられた不等式は
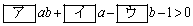
となる。左辺の因数分解を利用してxの範囲を求めると
 または
または 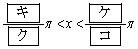
である。
[2] 不等式
[解答へ]
[2] 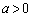 として、xの関数
として、xの関数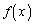 と
と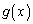 を
を
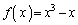
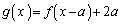
とする。
(1) 二つの関数の差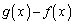 は
は 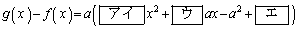
と表され、xの方程式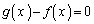 が異なる二つの実数解をもつようなaの範囲は
が異なる二つの実数解をもつようなaの範囲は
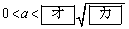
である。
また、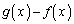 は
は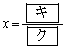 のとき、最大値
のとき、最大値

をとる。 (2) (1)で得られた最大値を
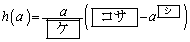
と表す。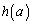 をaの関数と考えるとき、
をaの関数と考えるとき、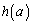 は
は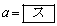 で最大値
で最大値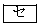 をとる。
をとる。 (3) 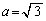 のとき、曲線
のとき、曲線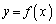 と曲線
と曲線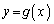 の二つの交点P,Qの座標は
の二つの交点P,Qの座標は P ,Q
,Q であり、二つの曲線
であり、二つの曲線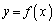 ,
,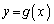 で囲まれた部分の面積Sは
で囲まれた部分の面積Sは
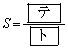
である。
さらに、交点P における曲線
における曲線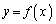 の接線と曲線
の接線と曲線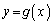 の接線がなす角をθ (
の接線がなす角をθ (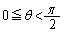 )とすると
)とすると
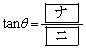
である。 [解答へ]
[3] 三つの数列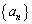 ,
,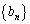 ,
,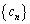 がある。
がある。
(1) 数列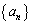 は、初項が
は、初項が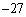 で、漸化式
で、漸化式 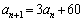 (
(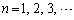 )を満たすとする。このとき
)を満たすとする。このとき
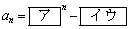
である。数列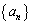 の初項から第n項までの和
の初項から第n項までの和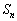 は
は
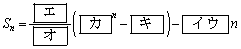
である。また、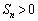 となる最小の自然数nは
となる最小の自然数nは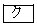 である。
である。
(2) 第n項が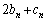 で与えられる数列
で与えられる数列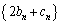 は、初項が0で公差がdの等差数列になり、第n項が
は、初項が0で公差がdの等差数列になり、第n項が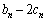 で与えられる数列
で与えられる数列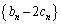 は、初項がxで公比がrの等比数列になるとする。このとき
は、初項がxで公比がrの等比数列になるとする。このとき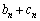 は
は 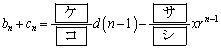
と表される。
(3) 数列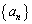 ,
,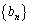 ,
,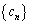 は(1),(2)を満たすとする。さらに、第n項が
は(1),(2)を満たすとする。さらに、第n項が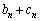 で与えられる数列
で与えられる数列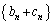 の階差数列は、数列
の階差数列は、数列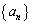 であるとする。このとき
であるとする。このとき 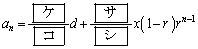
であるから、(1)より
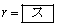 ,
,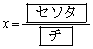 ,
,
である。したがって、数列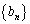 ,
,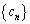 の第n項は、それぞれ
の第n項は、それぞれ
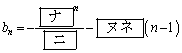
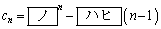
である。 [解答へ]
[4] 点Oを原点とする座標空間に4点A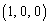 ,B
,B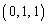 ,C
,C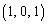 ,D
,D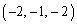 がある。
がある。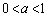 とし、線分ABをa:
とし、線分ABをa: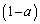 に内分する点をE,線分CDをa:
に内分する点をE,線分CDをa: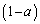 に内分する点をFとする。
に内分する点をFとする。
(1)  はaを用いて
はaを用いて 
と表される。さらに、 が
が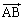 に垂直であるのは
に垂直であるのは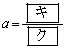 のときである。
のときである。 (2) 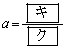 とする。
とする。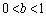 として、線分EFをb:
として、線分EFをb: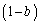 に内分する点をGとすると、
に内分する点をGとすると、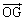 はbを用いて
はbを用いて 
と表される。 (3) (2)において、直線OGと直線BCが交わるときのbの値と、その交点Hの座標を求めよう。
点Hは直線BC上にあるから、実数sを用いて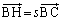 と表される。また、ベクトル
と表される。また、ベクトル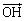 は実数tを用いて
は実数tを用いて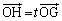 と表される。よって
と表される。よって
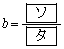 ,
,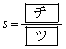 ,
,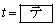
である。したがって、点Hの座標は
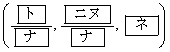
である。また、点Hは線分BCを :1に外分する。
:1に外分する。 [解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。