センター数学IIB '07年第2問
として、xの関数
と
を
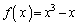
とする。
(1) 二つの関数の差
は 
と表され、xの方程式
が異なる二つの実数解をもつようなaの範囲は
である。
また、
は
のとき、最大値
をとる。 (2) (1)で得られた最大値を
と表す。
をaの関数と考えるとき、
は
で最大値
をとる。 (3) 
のとき、曲線
と曲線
の二つの交点P，Qの座標は P
，Q
であり、二つの曲線
，
で囲まれた部分の面積Sは
である。
さらに、交点P
における曲線
の接線と曲線
の接線がなす角をθ (
)とすると
である。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 単なる計算問題ですが、ボリュームがあるので、計算速度が問われます。
(ア)〜(エ)をミスすると全滅になるので、ここを丁寧に何度も確認してください。
の展開をミスしたばかりに、ペースを崩し、東大どころか、センター試験以降の入試を全て失敗してしまう、という悪夢が起こりうるのです。
途中で枠にはまらなくなったら、必ず、一番最初から見直すこと。
(1) 
(アイ) −3 (ウ) 3 (エ) 3
とすると、
これの判別式Dが
より(2次方程式の一般論を参照)、
より、
(オ) 2 (カ) 3 ......[答]
これは、
のとき、最大値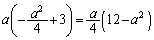
をとります(2次関数の最大最小を参照)。(キ) a (ク) 2 (ケ) 4 (コサ) 12 (シ) 2 ......[答]
(2) 
増減表より、
のとき、最大値は4 (3次関数の最大最小を参照)
(ス) 2 (セ) 4 ......[答]
(3) 
のとき、 
∴ 
，
より、
交点は、P
，Q
(ソ) 0 (タ) 3 (チ) 2 (ツ) 3 ......[答]二つの曲線
，
で囲まれた部分は、
の範囲にあり、この範囲において、
(
は、この範囲内で正の最大値
をとります)であることから、求める面積は(定積分と面積を参照)、
(テ) 9 (ト) 2 ......[答]
P
における、曲線
の接線の傾きを
，曲線
の接線の傾きを
として、
，
，
ここで、両接線のなす角
の正接を、
(正接の加法定理を参照)として計算すると、
になっているので、
(
)として、
(ナ) 9 (ニ) 7 ......[答]ここで、不運にも、
と計算した場合には、
は鈍角なので、
という条件に合わせて、補角の方を考え、
を解答にします。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
