�@�Z���^�[���wIIB '07�N��3��@
�O�̐���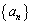 �C
�C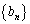 �C
�C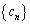 ������B
������B
(1) ����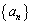 �́A������
�́A������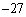 �ŁA�Q����
�ŁA�Q���� �@�@�@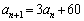 �@(
�@( )�����Ƃ���B���̂Ƃ�
)�����Ƃ���B���̂Ƃ�
�@�@�@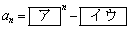
�ł���B����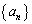 �̏��������n���܂ł̘a
�̏��������n���܂ł̘a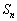 ��
��
�@�@�@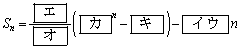
�ł���B�܂��A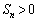 �ƂȂ�ŏ��̎��R��n��
�ƂȂ�ŏ��̎��R��n��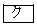 �ł���B
�ł���B
(2) ��n����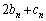 �ŗ^�����鐔��
�ŗ^�����鐔��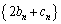 �́A������0�Ō�����d�̓�������ɂȂ�A��n����
�́A������0�Ō�����d�̓�������ɂȂ�A��n����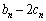 �ŗ^�����鐔��
�ŗ^�����鐔��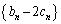 �́A������x�Ō��䂪r�̓��䐔��ɂȂ�Ƃ���B���̂Ƃ�
�́A������x�Ō��䂪r�̓��䐔��ɂȂ�Ƃ���B���̂Ƃ�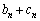 ��
�� �@�@�@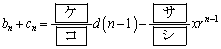
�ƕ\�����B
(3) ����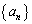 �C
�C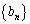 �C
�C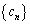 ��(1)�C(2)�����Ƃ���B����ɁA��n����
��(1)�C(2)�����Ƃ���B����ɁA��n����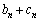 �ŗ^�����鐔��
�ŗ^�����鐔��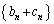 �̊K������́A����
�̊K������́A����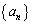 �ł���Ƃ���B���̂Ƃ�
�ł���Ƃ���B���̂Ƃ� �@�@�@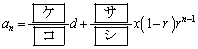
�ł��邩��A(1)���
�@�@�@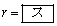 �C
�C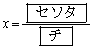 �C
�C
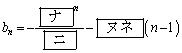
�ł���B���������āA����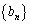 �C
�C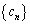 �̑�n���́A���ꂼ��
�̑�n���́A���ꂼ��
�@�@�@
�@�@�@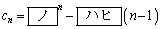
�ł���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
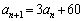 �@����@�@(
�@����@�@(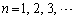 )�ɂ����āA
)�ɂ����āA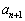 �C
�C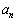 ��x�ɒu�������A
��x�ɒu�������A
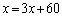 �@����A
�@����A
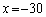
�@�|�A�����ƁA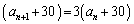
����́A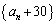 ���A�����F
���A�����F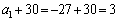 �C����F3�����䐔���ł��邱�Ƃ��Ӗ����܂��B
�C����F3�����䐔���ł��邱�Ƃ��Ӗ����܂��B
�� 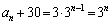 ��
�� 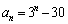 �@����B(�A) 3�@(�C�E) 30�@......[��]����
�@����B(�A) 3�@(�C�E) 30�@......[��]����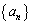 �̏��������n���܂ł̘a
�̏��������n���܂ł̘a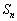 ��(���䐔�����Q��)�A
��(���䐔�����Q��)�A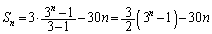 (�G) 3�@(�I) 2�@(�J) 3�@(�L) 1�@......[��]
(�G) 3�@(�I) 2�@(�J) 3�@(�L) 1�@......[��]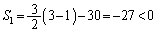 �C
�C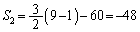 �C
�C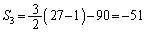 �C
�C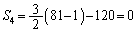 �C
�C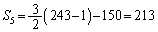
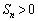 �ƂȂ�ŏ��̎��R��n��5
�ƂȂ�ŏ��̎��R��n��5
(�N) 5�@......[��]
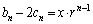 �@����D
�@����D
�C�~2�{�D���A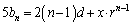
�� 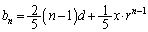 �@����E
�@����E
�C�|�D�~2���A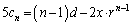
�� 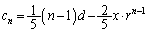 �@����E
�@����E
�D�{�E���A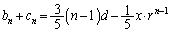 �@����F(�P) 3�@(�R) 5�@(�T) 1�@(�V) 5�@......[��]
�@����F(�P) 3�@(�R) 5�@(�T) 1�@(�V) 5�@......[��]
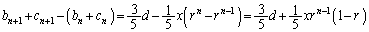 ���ꂪ�A
���ꂪ�A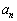 �ɓ������̂ŁA�B���A
�ɓ������̂ŁA�B���A
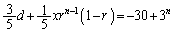
���ӂ�����ׂāA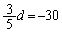
�� 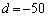
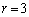
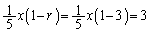 ��
�� 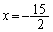
(�X) 3�@(�Z�\�^) �|15�@(�`) 2�@(�c�e�g) �|50�@......[��]�E���A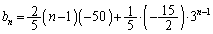
�� 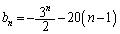 �F���A
�F���A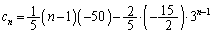
�� 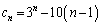
(�i) 3�@(�j) 2�@(�k�l) 20�@(�m) 3�@(�n�q) 10�@......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 