センター数学IIB '08年第2問
aを正の実数とし、xの2次関数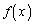 ,
,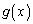 を
を
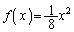
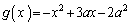
とする。また、放物線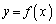 および
および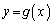 をそれぞれ
をそれぞれ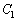 ,
,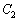 とする。
とする。
(1) 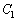 と
と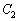 の共有点をPとすると、点Pの座標は
の共有点をPとすると、点Pの座標は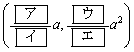 である。また、点Pにおける
である。また、点Pにおける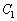 の接線の方程式は
の接線の方程式は 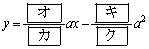
である。
(2)  とx軸および直線
とx軸および直線 で囲まれた図形の面積は
で囲まれた図形の面積は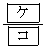 である。また、
である。また、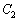 とx軸の交点のx座標は
とx軸の交点のx座標は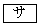 ,
, であり、
であり、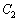 とx軸で囲まれた図形の面積は
とx軸で囲まれた図形の面積は である。
である。
(3) 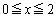 の範囲で、二つの放物線
の範囲で、二つの放物線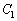 ,
,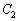 と2直線
と2直線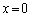 ,
,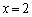 で囲まれた図形をRとする。Rの中で、
で囲まれた図形をRとする。Rの中で、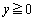 を満たすすべての部分の面積
を満たすすべての部分の面積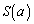 は
は である。したがって、aが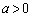 の範囲を動くとき、
の範囲を動くとき、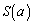 は
は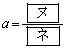 で最小値
で最小値 をとる。
をとる。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 こういう問題は、私には賛成できません。いかに手抜きをして要領よく計算するかというずる賢さが問われているわけで、まるで、世渡り上手なお役人さんを奨励しているような問題です。以下の解答のように丁寧にやっていては、他の問題にかける時間がなくなります。
(1) 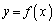 と
と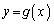 を連立すると、
を連立すると、 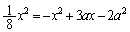
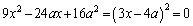 ∴
∴ 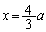 (重解だということは、
(重解だということは、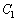 ,
,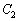 は接しているということです)
は接しているということです)このとき、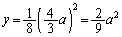
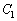 ,
,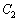 の共有点(接点)Pの座標は、
の共有点(接点)Pの座標は、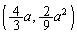 (ア) 4 (イ) 3 (ウ) 2 (エ) 9 ......[答]
(ア) 4 (イ) 3 (ウ) 2 (エ) 9 ......[答]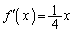 ,
,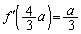 より、点Pにおける
より、点Pにおける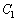 の接線(実は、共通接線です)は、
の接線(実は、共通接線です)は、 (オ) 1 (カ) 3 (キ) 2 (ク) 9 ......[答]
(2) 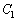 とx軸および直線
とx軸および直線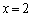 で囲まれた図形Fの面積は、
で囲まれた図形Fの面積は、 (ケ) 1 (コ) 3 ......[答]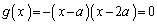 とすると、
とすると、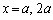 (サ) a (シス)
(サ) a (シス) 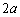 ......[答]
......[答]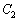 とx軸で囲まれた図形Gの面積は、
とx軸で囲まれた図形Gの面積は、 (セ) 1 (ソ) 6 ......[答]
(3) 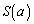 の計算は、図形Gが、
の計算は、図形Gが、 (iii) 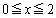 から全部が右側に出てしまう(
から全部が右側に出てしまう(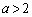 )
) の3つの場合に分けて行います。
(タ) 1 (チ) 2 ......[答]
(i) 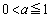 の場合は、
の場合は、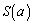 は、図形Fの面積から図形Gの面積を引いたものとなり、
は、図形Fの面積から図形Gの面積を引いたものとなり、 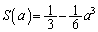 (問題文に書いてあります)
(問題文に書いてあります)(iii) 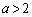 の場合は、
の場合は、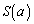 は、図形Fの面積に等しく、
は、図形Fの面積に等しく、 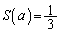 (問題文に書いてあります)
(問題文に書いてあります)(ii) 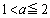 の場合、
の場合、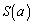 は、図形Fの面積から、
は、図形Fの面積から、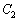 :
: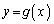 とx軸と直線
とx軸と直線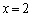 で囲む面積を引いたものになり、
で囲む面積を引いたものになり、 (ツ) 5 (テ) 6 (ト) 4 (ナ) 6 (ニ) 3 ......[答]
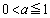 における最小値は、
における最小値は、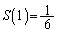 です。
です。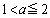 においては、
においては、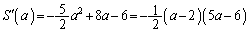
増減表より、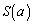 は、
は、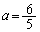 で最小値
で最小値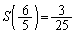 をとります(3次関数の最大最小を参照)。(ヌ) 6 (ネ) 5 (ノ) 3 (ハヒ) 25 ......[答]注意 センター試験の会場では、
をとります(3次関数の最大最小を参照)。(ヌ) 6 (ネ) 5 (ノ) 3 (ハヒ) 25 ......[答]注意 センター試験の会場では、 最小は、引く方の面積:
最小は、引く方の面積: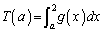 が最大のときと最初から決めつけて計算してください。最小値は、
が最大のときと最初から決めつけて計算してください。最小値は、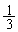 から
から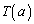 の最大値
の最大値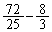 (通分しないでおく)を引いて求めます。
(通分しないでおく)を引いて求めます。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。  である。また、点Pにおける
である。また、点Pにおける