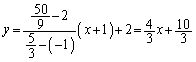�@�Z���^�[���wIIB '09�N��2��@
������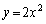 ��C�C�_
��C�C�_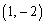 ��A�Ƃ���B
��A�Ƃ���B
�_Q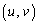 �Ɋւ��āA�_A�ƑΏ̂ȓ_��P
�Ɋւ��āA�_A�ƑΏ̂ȓ_��P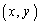 �Ƃ���ƁA
�Ƃ���ƁA
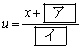 �C
�C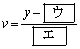
�ł���B
��̕�����C��D�̌�_��R��S�Ƃ���B�������Ax���W�̏���������R�Ƃ���B�_R�CS��x���W�͂��ꂼ�� �C
�C �ŁA�_R�CS�ɂ����������D�̐ڐ��̕������͂��ꂼ��
�ŁA�_R�CS�ɂ����������D�̐ڐ��̕������͂��ꂼ��
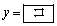 �C
�C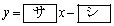
P�������D��̓_�Ƃ��AP��x���W��a�Ƃ����BP����x���Ɉ����������ƕ�����C�Ƃ̌�_��H�Ƃ���B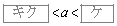 �̂Ƃ��A�O�p�`PHR�̖ʐ�
�̂Ƃ��A�O�p�`PHR�̖ʐ�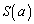 ��
��
�ƕ\�����B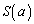 ��
��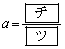 �̂Ƃ��A�ő�l���Ƃ�B
�̂Ƃ��A�ő�l���Ƃ�B
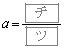 �̂Ƃ��A����HR�ƕ�����D�̌�_�̂����AR�ƈقȂ�_��x���W��
�̂Ƃ��A����HR�ƕ�����D�̌�_�̂����AR�ƈقȂ�_��x���W��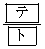 �ł���B���̂Ƃ��A
�ł���B���̂Ƃ��A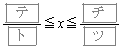 �͈̔͂ŁA������D�ƒ���PH����ђ���HR�ň͂܂ꂽ�}�`�̖ʐς�
�͈̔͂ŁA������D�ƒ���PH����ђ���HR�ň͂܂ꂽ�}�`�̖ʐς� �ł���B
�ł���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�S���̗\���Z�T�C�g�⍂�Z�̐搶���̒c�̂ł́A������������K�ȗǖ�Ǝ����グ��̂ł��傤����ǂ��A�����������̂��߂ɖ���ł��ӂ���Ă��܂��˔\���v���ƁA���E�F�u�T�C�g�́A���N�J��Ԃ���Ă��邱������������ꍏ��������߂�ׂ����A�ƁA�咣�v���܂��B
�v�Z�̃{�����[��������̂ɁA�O���̃~�X���ꐶ��_�ɐU��v�����ɂȂ��Ă��܂��̂ŁA��֍������ڎw���F����́A���Z���@�Ȃǂ��H�v����ƂƂ��ɁA�{�Ԃł͑O�����~�X���Ȃ��悤�ɏ[���ɒ��ӂ��Ă��������B�������Ԃ��l����ƁA����I�ɂ͍Ō��(�i)�`(�m)���p�X���邱�Ƃ������ł��B
P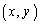 ��A
��A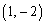 �̒��_��Q
�̒��_��Q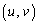 �ɂȂ�܂��B
�ɂȂ�܂��B
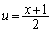 �C
�C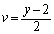
Q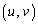 ��C����̂ŁA
��C����̂ŁA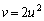 ���A
���A
�������āA
D�F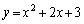 �@����@
�@����@ (�I) 2�@(�J) 3 ......[��]
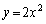 �ƘA������ƁA
�ƘA������ƁA
�������āA
�� 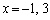
(�L) �|�@(�N) 1�@(�P) 3 ......[��]
�@��������āA
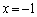 �̂Ƃ��A
�̂Ƃ��A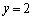 �C
�C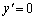
R�ɂ������ڐ��́A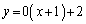
�� 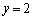
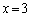 �̂Ƃ��A
�̂Ƃ��A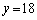 �C
�C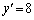
S�ɂ�����ڐ��́A
�� 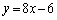
(�R) 2�@(�T) 8�@(�V) 6 ......[��]
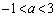 �ɂ����ẮA
�ɂ����ẮA
�Ȃ̂ŁAD��C�̏�ɗ��܂��BP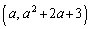 �CH
�CH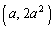 ���A�O�p�`PHR�̒��PH�́A
���A�O�p�`PHR�̒��PH�́A
�O�p�`PHR�̍����́AP��R��x���W�̍���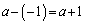
�� 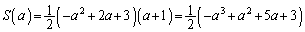
(�X) 2�@(�Z) �|�@(�\) 5�@(�^) 3
 �����\���A
�����\���A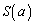 ��
��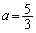 �̂Ƃ��A�ő�l���Ƃ�܂�(3�����̍ő�ŏ����Q��)�B
�̂Ƃ��A�ő�l���Ƃ�܂�(3�����̍ő�ŏ����Q��)�B
(�`) 5�@(�c) 3 ......[��]
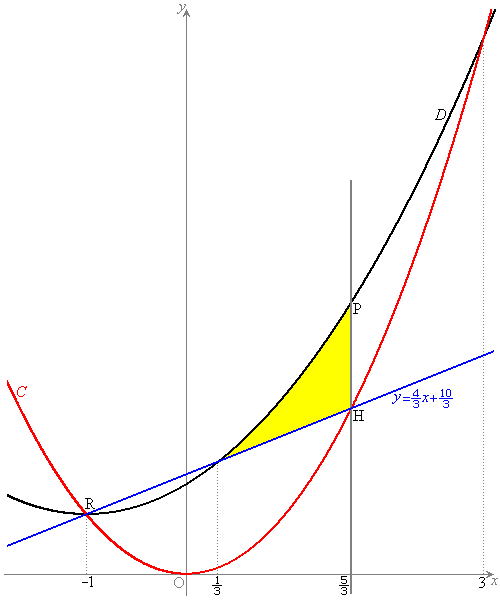
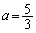 �̂Ƃ��AH�̍��W��
�̂Ƃ��AH�̍��W��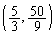 �ƂȂ�܂��BR
�ƂȂ�܂��BR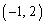 ��H�����������́A
��H�����������́A
����Ƈ@��A�����āA
�������āA
�� 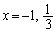
R�ƈقȂ��_��x���W��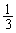 �ł��B
�ł��B
(�e) 1�@(�g) 3 ......[��]
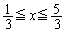 �͈̔͂ŁA������D�ƒ���PH (
�͈̔͂ŁA������D�ƒ���PH (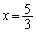 )����ђ���HR�ň͂܂ꂽ�}�`(�E�}�̉��F���F����)���ʐ��́A
)����ђ���HR�ň͂܂ꂽ�}�`(�E�}�̉��F���F����)���ʐ��́A
(�i) 1�@(�j) 6�@(�k) 0�@(�l) 8�@(�m) 1 ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B