センター試験数学IIB 2010年問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1][1] 連立方程式
(*) 
を満たす正の実数x,yを求めよう。ただし、 ,
,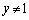 とする。①の両辺で2を底とする対数をとると
とする。①の両辺で2を底とする対数をとると が成り立つ。これと②より
である。
したがって、 ,
, は2次方程式
は2次方程式  ・・・③
・・・③の解である。③の解は である。ただし、
である。ただし、 ,
, は解答の順序を問わない。よって、連立方程式(*)の解は
は解答の順序を問わない。よって、連立方程式(*)の解は
 または
または である。
である。 [2]  の範囲で
の範囲で  ・・・①
・・・①を満たすθ と の値を求めよう。
の値を求めよう。
一般に、すべてのxについて である。 に当てはまるものを、次の
に当てはまるものを、次の ~
~ のうちから一つ選べ。
のうちから一つ選べ。




 したがって、①が成り立つとき、
したがって、①が成り立つとき、 となり、
となり、 の範囲で
の範囲で ,
, のとり得る値の範囲を考えれば、
のとり得る値の範囲を考えれば、 または
または となる。よって、①を満たすθ は
となる。よって、①を満たすθ は または
または である。
である。
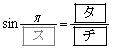 である。
である。 の値を求めよう。①より
の値を求めよう。①より となり、この式の左辺を2倍角の公式を用いて変形すれば
となる。ここで であるから
であるから  ・・・②
・・・②が成り立つ。 は②を満たしている。
は②を満たしている。 とすると、
とすると、 であるから
であるから となる。ここで、 より
より である。
[解答へ]
[2] kを実数とし、座標平面上に点P をとる。曲線
をとる。曲線
をCとする。
(1) 点Q における曲線Cの接線が点Pを通るとすると
における曲線Cの接線が点Pを通るとすると が成り立つ。

とおくと、関数 は
は で極小値
で極小値 をとり、
をとり、 で極大値
で極大値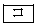 をとる。
をとる。
したがって、点Pを通る曲線Cの接線の本数がちょうど2本となるのは、kの値が または
または のときである。また、点Pを通る曲線Cの接線の本数は
のときである。また、点Pを通る曲線Cの接線の本数は のとき
のとき 本、
本、 のとき
のとき 本、
本、 のとき
のとき 本となる。
本となる。 (2)  とする。曲線
とする。曲線 をDとする。曲線CとDの交点のx座標は と
と である。
である。
 の範囲において、2曲線C,Dおよび2直線
の範囲において、2曲線C,Dおよび2直線 ,
, で囲まれた二つの図形の面積の和は
で囲まれた二つの図形の面積の和は である。
である。 [解答へ]
[3] 自然数の列1,2,3,4,・・・ を、次のように群に分ける。
1 | 2,3,4,5 | 6,7,8,9,10,11,12 | ・・・
ここで、一般に第n群は 個の項からなるものとする。第n群の最後の項を
個の項からなるものとする。第n群の最後の項を で表す。
で表す。
 (
(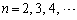 )
)が成り立ち
 (
( )
)である。
よって、600は、第 群の小さい方から
群の小さい方から 番目の項である。
番目の項である。 (2)  に対し、第
に対し、第 群の小さい方から
群の小さい方から 番目の項を
番目の項を で表すと
で表すと であり
が成り立つ。これより
 (
( )
)となる。
[解答へ]
 [4] 二つずつ平行な三組の平面で囲まれた立体を平行六面体という。辺の長さがすべて1の平行六面体ABCD-EFGHがあり、
[4] 二つずつ平行な三組の平面で囲まれた立体を平行六面体という。辺の長さがすべて1の平行六面体ABCD-EFGHがあり、 ,
, である。
である。 ,
, ,
, とおく。
とおく。
 ,
, とする。辺ABをa:
とする。辺ABをa: の比に内分する点をX,辺BFをb:
の比に内分する点をX,辺BFをb: の比に内分する点をYとする。点Xを通り直線AHに平行な直線と辺GHとの交点をZとする。三角形XYZを含む平面をαとする。
の比に内分する点をYとする。点Xを通り直線AHに平行な直線と辺GHとの交点をZとする。三角形XYZを含む平面をαとする。
(1)  ,
,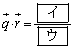 である。ベクトル
である。ベクトル は、a,b,
は、a,b, ,
,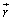 を用いて
を用いて と表される。
と表される。  である。
である。(2) 直線ECと平面αが垂直に交わるとし、交点をKとする。 が三角形XYZの2辺と垂直であることから、
が三角形XYZの2辺と垂直であることから、 が成り立つ。
が成り立つ。 以下では、 とする。このとき
とする。このとき である。
である。 を実数cを用いて
を実数cを用いて と表すと、
と表すと、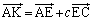 である。一方、点Kは平面α上にあるから、
である。一方、点Kは平面α上にあるから、 は実数s,tを用いて
は実数s,tを用いて [解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 




 となる。
となる。