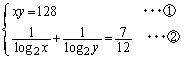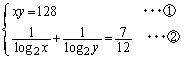センター数学IIB '10年第1問
[1] 連立方程式
(*) 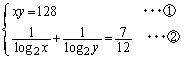
を満たす正の実数x,yを求めよう。ただし、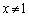 ,
,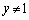 とする。①の両辺で2を底とする対数をとると
とする。①の両辺で2を底とする対数をとると が成り立つ。これと②より
である。
したがって、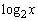 ,
,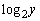 は2次方程式
は2次方程式 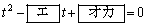 ・・・③
・・・③の解である。③の解は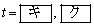 である。ただし、
である。ただし、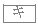 ,
,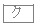 は解答の順序を問わない。よって、連立方程式(*)の解は
は解答の順序を問わない。よって、連立方程式(*)の解は
 または
または である。
である。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 対数方程式に関する基本問題です。なお、対数関数を参照してください。
①の両辺で2を底とする対数をとると
これと、②より、
∴ 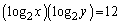
(ア) 7 (イ) 1 (ウ) 2 ......[答]
従って、解と係数の関係より、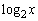 ,
,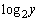 は2次方程式
は2次方程式
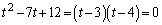 ・・・③
・・・③
③の解は、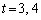
従って、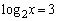 ,
,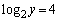 ,または、
,または、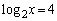 ,
,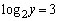
即ち、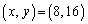 または
または 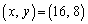
(エ) 7 (オ) 1 (カ) 2 (キ) 3 (ク) 4 (ケ) 8 (コ) 1 (サ) 6 ......[答]
注.問題文の指定より、(キ) 4 (ク) 3でも正解です。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[2] 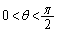 の範囲で
の範囲で 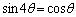 ・・・①
・・・①を満たすθ と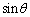 の値を求めよう。
の値を求めよう。
一般に、すべてのxについて である。 に当てはまるものを、次の
に当てはまるものを、次の ~
~ のうちから一つ選べ。
のうちから一つ選べ。
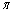

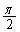

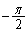 したがって、①が成り立つとき、
したがって、①が成り立つとき、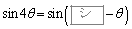 となり、
となり、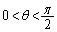 の範囲で
の範囲で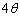 ,
,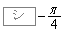 のとり得る値の範囲を考えれば、
のとり得る値の範囲を考えれば、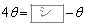 または
または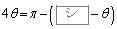 となる。よって、①を満たすθ は
となる。よって、①を満たすθ は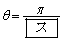 または
または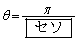 である。
である。
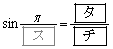 である。
である。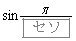 の値を求めよう。①より
の値を求めよう。①より となり、この式の左辺を2倍角の公式を用いて変形すれば
となる。ここで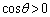 であるから
であるから  ・・・②
・・・②が成り立つ。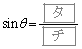 は②を満たしている。
は②を満たしている。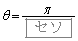 とすると、
とすると、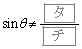 であるから
であるから となる。ここで、 より
より である。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 三角関数の問題ですが、問題文が錯綜しているので、読み間違いに注意しましょう。
より、一般に、すべてのxについて、
が成り立ちます。
(シ) 
①が成り立つとき、
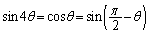 ・・・③
・・・③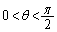 の範囲で
の範囲で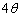 ,
,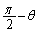 のとり得る値の範囲は、
のとり得る値の範囲は、
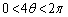 ,
,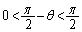
ここで、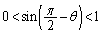 ですが、
ですが、
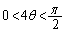 ,
,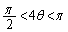 のいずれにおいても、
のいずれにおいても、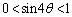 となるので、
となるので、
・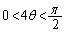 のとき、③より、
のとき、③より、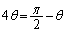
∴ 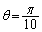
∴ 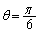
(ス) 6 (セ) 1 (ソ) 0 ......[答]
(タ) 1 (チ) 2 ......[答]
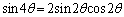 (2倍角の公式を参照)と①より、
(2倍角の公式を参照)と①より、
(ツ) 2 ......[答]
さらに、2倍角の公式を用いて変形すれば、
(テ) 4 (ト) 8 ......[答]
ここで、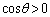 より、
より、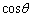 で両辺を割ることにより、
で両辺を割ることにより、
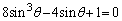 ・・・②
・・・②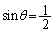 が②を満たすので、②左辺は
が②を満たすので、②左辺は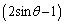 で割り切れます。割り算を実行することにより、
で割り切れます。割り算を実行することにより、
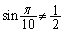 より、
より、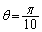 のとき
のとき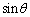 は、
は、
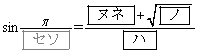
を満たします。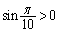 より、
より、
(ナ) 4 (ニ) 2 (ヌ) - (ネ) 1 (ノ) 5 (ハ) 4 ......[答]
数学TOP TOPページに戻る
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。