センター試験数学IIB 2012年問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1][1] 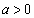 ,
,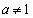 として、不等式
として、不等式
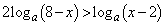 ・・・①
・・・①を満たすxの値の範囲を求めよう。
真数は正であるから、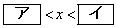 が成り立つ。ただし、対数
が成り立つ。ただし、対数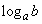 に対し、aを底といい、bを真数という。
に対し、aを底といい、bを真数という。
底aが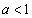 を満たすとき、不等式①
を満たすとき、不等式① 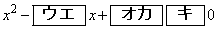 ・・・②
・・・②となる。ただし、 については、当てはまるものを、次の
については、当てはまるものを、次の ~
~ のうちから一つ選べ。
のうちから一つ選べ。
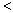

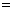

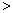 したがって、真数が正であることと②から、
したがって、真数が正であることと②から、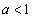 のとき、不等式①を満たすxのとり得る値の範囲は
のとき、不等式①を満たすxのとり得る値の範囲は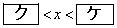 である。
である。
同様にして、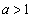 のときには、不等式①を満たすxのとり得る値の範囲は
のときには、不等式①を満たすxのとり得る値の範囲は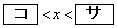 であることがわかる。
であることがわかる。
[2] 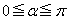 として
として を満たすβ について考えよう。ただし、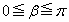 とする。
とする。
たとえば、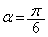 のとき、β のとり得る値は
のとき、β のとり得る値は と
と の二つである。
の二つである。
このように、αの各値に対して、β のとり得る値は二つある。そのうちの小さい方を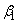 ,大きい方を
,大きい方を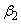 とし
とし が最大となるαの値とそのときのyの値を求めよう。
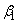 ,
,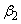 をαを用いて表すと、
をαを用いて表すと、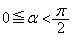 のときは
のときは 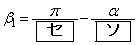 ,
,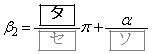
となり、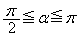 のときは
のときは 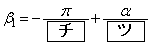 ,
,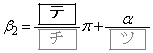
となる。
したがって、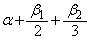 のとり得る値の範囲は
のとり得る値の範囲は である。よって、yが最大となるαの値は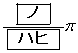 であり、そのときのyの値は
であり、そのときのyの値は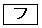 であることがわかる。
であることがわかる。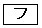 に当てはまるものを、次の
に当てはまるものを、次の ~
~ のうちから一つ選べ。
のうちから一つ選べ。
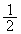
 1
1 
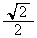

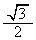
[解答へ]
[2] 座標平面上で曲線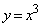 をCとし、放物線
をCとし、放物線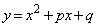 をDとする。
をDとする。
(1) 曲線C上の点P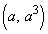 におけるCの接線の方程式は
におけるCの接線の方程式は である。放物線Dは点Pを通り、DのPにおける接線と、CのPにおける接線が一致するとする。このとき、pとqをaを用いて表すと
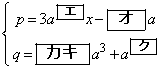 ・・・①
・・・①となる。
以下、p,qは①を満たすとする。
(2) 放物線Dがy軸上の与えられた点Q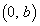 を通るとき
を通るとき 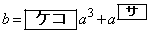 ・・・②
・・・②が成り立つ。与えられたbに対して、②を満たすaの値の個数を調べよう。
そのために、関数
の増減を調べる。関数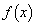 は、
は、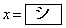 で極小値
で極小値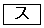 をとり、
をとり、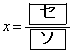 で極大値
で極大値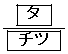 をとる。
をとる。
関数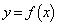 のグラフをかくことにより、
のグラフをかくことにより、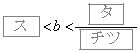 のとき、②を満たすaの値の個数は
のとき、②を満たすaの値の個数は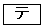 であることがわかる。
であることがわかる。
(3) 放物線Dの頂点がx軸上にあるのは、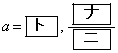 の二つの場合である。
の二つの場合である。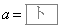 のときの放物線を
のときの放物線を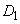 ,
,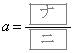 のときの放物線を
のときの放物線を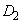 とする。
とする。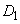 ,
,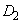 とx軸で囲まれた図形の面積は
とx軸で囲まれた図形の面積は である。
である。 [解答へ]
[3] 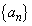 を
を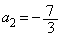 ,
,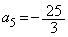 である等差数列とし、自然数nに対して、
である等差数列とし、自然数nに対して、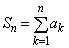 とおく。
とおく。
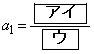 であり、
であり、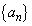 の公差は
の公差は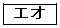 である。したがって
である。したがって
である。
次に、数列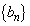 は
は
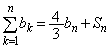 (
(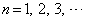 ) ・・・①
) ・・・①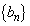 の一般項を求めよう。①から
の一般項を求めよう。①から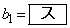 である。さらに、
である。さらに、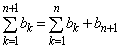 に注意して、①を利用すると
に注意して、①を利用すると
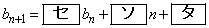 (
(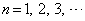 )
)
と変形できる。ここで
 (
(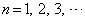 ) ・・・②
) ・・・②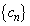 は、
は、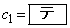 ,公比が
,公比が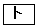 の等比数列であるから、②により
の等比数列であるから、②により
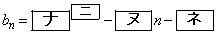 (
(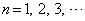 )
)
である。ただし、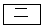 については、当てはまるものを、次の
については、当てはまるものを、次の ~
~ のうちから一つ選べ。
のうちから一つ選べ。

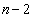

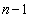
 n
n 
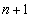

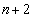
[解答へ]
[4] 空間に異なる4点O,A,B,Cを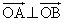 ,
,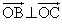 ,
,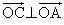 となるようにとり、
となるようにとり、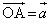 ,
,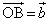 ,
,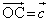 とおく。さらに、3点D,E,Fを、
とおく。さらに、3点D,E,Fを、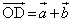 ,
,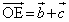 ,
,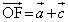 となるようにとり、線分BDの中点をL,線分CEの中点をMとし、線分ADを3:1に内分する点をNとする。
となるようにとり、線分BDの中点をL,線分CEの中点をMとし、線分ADを3:1に内分する点をNとする。
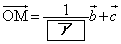 ,
,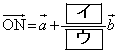
と表される。
(2) 2直線FL,MNが交わることを確かめよう。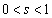 とし、線分FLをs:
とし、線分FLをs: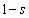 に内分する点をPとする。
に内分する点をPとする。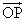 は、sと
は、sと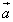 ,
,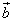 ,
,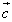 を用いて
を用いて と表される。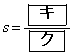 のとき、
のとき、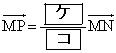 となるので、M,N,Pは一直線上にある。よって、2直線FL,MNは交わることがわかる。
となるので、M,N,Pは一直線上にある。よって、2直線FL,MNは交わることがわかる。
(3) 2直線FL,MNの交点をGとする。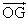 ,
,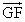 は、
は、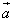 ,
,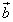 ,
,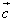 を用いて
を用いて と表される。
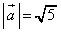 ,
,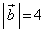 ,
,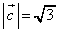 とする。このとき、
とする。このとき、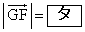 ,
,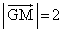 となる。
となる。
次に、直線OC上に点Hをとり、実数t を用いて、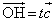 と表す。
と表す。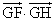 ,
,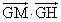 は、t を用いて
は、t を用いて 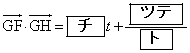 ・・・①
・・・①
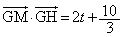 ・・・②
・・・②と表される。
さらに、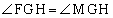 とする。このときのt の値を求めよう。
とする。このときのt の値を求めよう。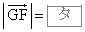 ,
,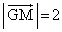 と
と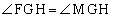 であることから
であることから 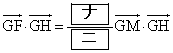 ・・・③
・・・③が成り立つ。①,②,③から、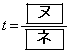 である。
である。 [解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。  の二つである。
の二つである。

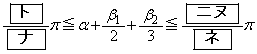
 であり、そのときのyの値は
であり、そのときのyの値は ・・・①
・・・①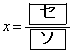 で極大値
で極大値 をとる。
をとる。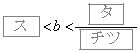 のとき、②を満たすaの値の個数は
のとき、②を満たすaの値の個数は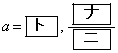 の二つの場合である。
の二つの場合である。 のときの放物線を
のときの放物線を である。
である。 であり、
であり、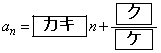 (
(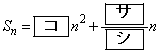 (
(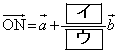
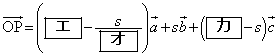
 のとき、
のとき、 となるので、M,N,Pは一直線上にある。よって、2直線FL,MNは交わることがわかる。
となるので、M,N,Pは一直線上にある。よって、2直線FL,MNは交わることがわかる。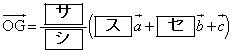
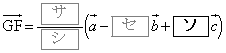
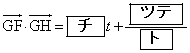 ・・・①
・・・① ・・・③
・・・③ である。
である。