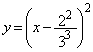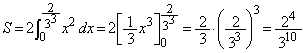センター数学IIB '12年第2問
座標平面上で曲線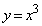 をCとし、放物線
をCとし、放物線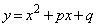 をDとする。
をDとする。
(1) 曲線C上の点P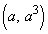 におけるCの接線の方程式は
におけるCの接線の方程式は である。放物線Dは点Pを通り、DのPにおける接線と、CのPにおける接線が一致するとする。このとき、pとqをaを用いて表すと
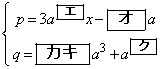 ・・・①
・・・①となる。
以下、p,qは①を満たすとする。
(2) 放物線Dがy軸上の与えられた点Q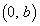 を通るとき
を通るとき 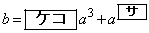 ・・・②
・・・②が成り立つ。与えられたbに対して、②を満たすaの値の個数を調べよう。
そのために、関数
の増減を調べる。関数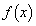 は、
は、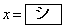 で極小値
で極小値 をとり、
をとり、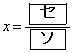 で極大値
で極大値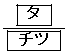 をとる。
をとる。
関数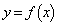 のグラフをかくことにより、
のグラフをかくことにより、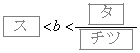 のとき、②を満たすaの値の個数は
のとき、②を満たすaの値の個数は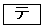 であることがわかる。
であることがわかる。
(3) 放物線Dの頂点がx軸上にあるのは、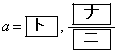 の二つの場合である。
の二つの場合である。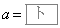 のときの放物線を
のときの放物線を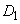 ,
,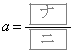 のときの放物線を
のときの放物線を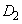 とする。
とする。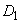 ,
,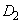 とx軸で囲まれた図形の面積は
とx軸で囲まれた図形の面積は である。
である。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 最後の面積のところの答え方に驚かされますが、数学Ⅱの微積分の基本問題です。
C: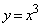 ・・・③D:
・・・③D: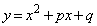 ・・・④
・・・④
(1) ③を微分して、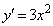
(ア) 2 (イ) 2 (ウ) 3 ......[答]④を微分して、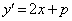 DのPにおける接線と、CのPにおける接線が等しいとき、両者の
DのPにおける接線と、CのPにおける接線が等しいとき、両者の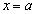 におけるy座標と接線の傾きが等しく、
におけるy座標と接線の傾きが等しく、 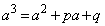 ・・・⑤
・・・⑤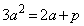
これより、
⑤に代入して、
∴ 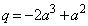
(エ) 2 (オ) 2 (カ) - (キ) 2 (ク) 2 ......[答]
(2) 放物線Dは、
Q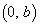 を通るので、
を通るので、 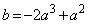 ・・・②
・・・②(ケ) - (コ) 2 (サ) 2 ......[答]
増減表より、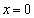 で極大値:0,
で極大値:0,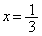 で極小値:
で極小値: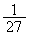 (3次関数の増減を参照)
(3次関数の増減を参照)
(シ) 0 (ス) 0 (セ) 1 (ソ) 3 (タ) 1 (チ) 2 (ツ) 7 ......[答]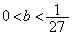 のとき、②を満たすaの値の個数は3。(テ) 3 ......[答]
のとき、②を満たすaの値の個数は3。(テ) 3 ......[答]
(3)⑥より、
放物線Dの頂点がx軸上にあるとき、
∴ 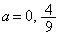
(ト) 0 (ナ) 4 (ニ) 9 ......[答]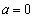 のとき、
のとき、 より、放物線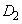 は
は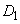 をx軸正方向に、
をx軸正方向に、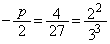 だけ平行移動した放物線で、
だけ平行移動した放物線で、 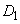 ,
,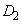 とx軸で囲まれた図形の面積Sは、放物線が軸に関して対称なことから、
とx軸で囲まれた図形の面積Sは、放物線が軸に関して対称なことから、(ヌ) 4 (ネ) 1 (ノ) 0 ......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。  ・・・①
・・・①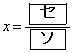 で極大値
で極大値 をとる。
をとる。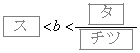 のとき、②を満たすaの値の個数は
のとき、②を満たすaの値の個数は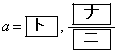 の二つの場合である。
の二つの場合である。 のときの放物線を
のときの放物線を である。
である。