�@�Z���^�[�������wIIB 2013�N���@
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
[1][1]�@O�����_�Ƃ�����W���ʏ��2�_A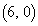 �CB
�CB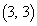 ���Ƃ�A����AB��2�F1�ɓ�������_��P�C1�F2�ɊO������_��Q�Ƃ���B3�_O�CP�CQ��ʂ�~��C�Ƃ���B
���Ƃ�A����AB��2�F1�ɓ�������_��P�C1�F2�ɊO������_��Q�Ƃ���B3�_O�CP�CQ��ʂ�~��C�Ƃ���B
(1) P�̍��W��( �C
�C )�ł���AQ�̍��W��(
)�ł���AQ�̍��W��( �C
�C )�ł���B
)�ł���B (2) �~C�̕����������̂悤�ɋ��߂悤�B����OP�̒��_��ʂ�AOP�ɐ����Ȓ����̕�������
�ł���A����PQ�̒��_��ʂ�APQ�ɐ����Ȓ����̕�������
�ł���B
������2�����̌�_���~C�̒��S�ł��邱�Ƃ���A�~C�̕�������
�ł��邱�Ƃ��킩��B
(3) �~C��x���̓�̌�_�̂����A�_O�ƈقȂ��_��R�Ƃ���ƁAR�͐���OA�� �F1�ɊO������B
�F1�ɊO������B
[2]�@�A��������
(��) 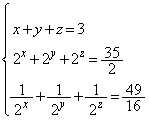
��������x�Cy�Cz�����߂悤�B�������A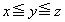 �Ƃ���B
�Ƃ���B
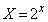 �C
�C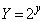 �C
�C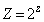 �Ƃ����ƁA
�Ƃ����ƁA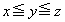 �ɂ��
�ɂ��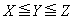 �ł���B(��)����AX�CY�CZ�̊W��
�ł���B(��)����AX�CY�CZ�̊W�� ��������B
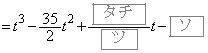
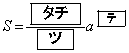
���̊W���𗘗p����ƁAt ��3����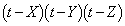 ��
�� �ƂȂ�B���������āA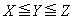 �ɂ��
�ɂ�� �ł���
[��]
[2]�@a�𐳂̎����Ƃ��āAx�̊�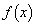 ��
��
�Ƃ���B
��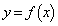 �́A
�́A �ŋɑ�l
�ŋɑ�l ���Ƃ�A
���Ƃ�A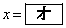 �ŋɏ��l
�ŋɏ��l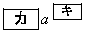 ���Ƃ�B���̂Ƃ��A2�_
���Ƃ�B���̂Ƃ��A2�_
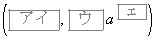 �C
�C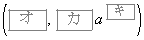
��C�Ƃ���B���_�ɂ�����C�̐ڐ�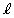 �̕�������
�̕�������
�ł���B�܂��A���_��ʂ�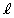 �ɐ����Ȓ���m�̕�������
�ɐ����Ȓ���m�̕�������
�ł���B
x���Ɋւ��ĕ�����C�ƑΏ̂ȕ�����
��D�Ƃ���BD��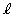 �ň͂܂ꂽ�}�`�̖ʐ�S��
�ň͂܂ꂽ�}�`�̖ʐ�S��
�ł���B
������C�ƒ���m�̌�_��x���W�́A0��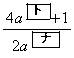 �ł���BC��m�ň͂܂ꂽ�}�`�̖ʐς�T�Ƃ���B
�ł���BC��m�ň͂܂ꂽ�}�`�̖ʐς�T�Ƃ���B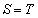 �ƂȂ�̂�
�ƂȂ�̂�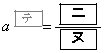 �̂Ƃ��ł���A���̂Ƃ��A
�̂Ƃ��ł���A���̂Ƃ��A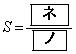 �ł���B
�ł���B
[��]
[3](1) ����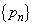 �͎������Ƃ���B
�͎������Ƃ���B
����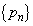 �̈�ʍ��ƁA���������n���܂ł̘a�����߂悤�B�܂��A�@����
�̈�ʍ��ƁA���������n���܂ł̘a�����߂悤�B�܂��A�@���� 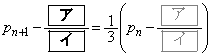 �@(
�@(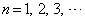 )
)�ƂȂ�̂ŁA����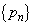 �̈�ʍ���
�̈�ʍ��� �ł���B���������āA���R��n�ɑ���
�ł���B
(2) ���̐�����Ȃ鐔��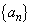 �́A���������3����
�́A���������3����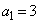 �C
�C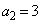 �C
�C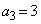 �ł���A���ׂĂ̎��R��n�ɑ���
�ł���A���ׂĂ̎��R��n�ɑ��� 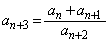 �@����A
�@����A�����Ƃ���B�܂��A����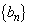 �C
�C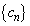 ���A���R��n�ɑ��āA
���A���R��n�ɑ��āA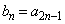 �C
�C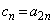 �Œ�߂�B����
�Œ�߂�B����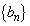 �C
�C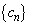 �̈�ʍ������߂悤�B�܂��A�A����
�̈�ʍ������߂悤�B�܂��A�A���� �ł���B���������āA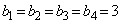 �ƂȂ�̂�
�ƂȂ�̂� 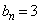 �@(
�@(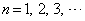 )�@����B
)�@����B�Ɛ���ł���B
�B���������߂ɂ́A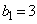 ����A���ׂĂ̎��R��n�ɑ���
����A���ׂĂ̎��R��n�ɑ��� 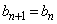 �@����C
�@����C�ł��邱�Ƃ������Ηǂ��B���̂��Ƃ��u�܂��A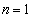 �̂Ƃ��C�����藧���Ƃ������A���ɁA
�̂Ƃ��C�����藧���Ƃ������A���ɁA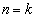 �̂Ƃ��C�����藧�Ɖ��肷��ƁA
�̂Ƃ��C�����藧�Ɖ��肷��ƁA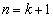 �̂Ƃ����C�����藧���Ƃ��������@�v��p���ďؖ����悤�B���̕��@��
�̂Ƃ����C�����藧���Ƃ��������@�v��p���ďؖ����悤�B���̕��@��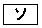 �Ƃ����B
�Ƃ����B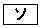 �ɓ��Ă͂܂���̂��A����
�ɓ��Ă͂܂���̂��A���� �`
�` �̂��������I�ׁB
�̂��������I�ׁB
 �@�g�����@�@�@
�@�g�����@�@�@ �@�ʓx�@�@�@
�@�ʓx�@�@�@ �@���w�I�A�[�@�@�@
�@���w�I�A�[�@�@�@ �@�w���@
�@�w���@
[�T]�@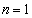 �̂Ƃ��A
�̂Ƃ��A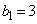 �C
�C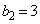 �ł��邱�Ƃ���C�͐��藧�B
�ł��邱�Ƃ���C�͐��藧�B [�U]�@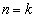 �̂Ƃ��A�C�����藧�A���Ȃ킿�A
�̂Ƃ��A�C�����藧�A���Ȃ킿�A 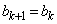 �@����D
�@����D�Ɖ��肷��B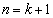 �̂Ƃ��A�A��n��
�̂Ƃ��A�A��n��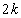 �������ē����铙���ƁA
�������ē����铙���ƁA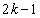 �������ē����铙������
�������ē����铙������ 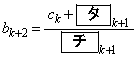 �C
�C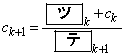
�ƂȂ�̂ŁA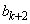 ��
�� �ƕ\�����B���������āA�D�ɂ��A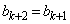 �����藧�̂ŁA�C��
�����藧�̂ŁA�C��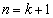 �̂Ƃ��ɂ����藧�B[�T]�C[�U]�ɂ��A���ׂĂ̎��R��n�ɑ��ćC�̐��藧���Ƃ��ؖ����ꂽ�B
�̂Ƃ��ɂ����藧�B[�T]�C[�U]�ɂ��A���ׂĂ̎��R��n�ɑ��ćC�̐��藧���Ƃ��ؖ����ꂽ�B
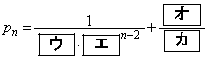
���������āA�B�����藧�̂ŁA����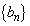 �̈�ʍ���
�̈�ʍ���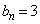 �ł���B
�ł���B
���ɁA�A��n��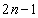 �ɒu�������ē����铙���ƇB����
�ɒu�������ē����铙���ƇB���� �ƂȂ�A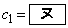 �ł��邱�ƂƇ@����A����
�ł��邱�ƂƇ@����A���� �̈�ʍ��́A(1)�ŋ��߂�����
�̈�ʍ��́A(1)�ŋ��߂�����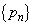 �̈�ʍ��Ɠ������Ȃ邱�Ƃ��킩��B
�̈�ʍ��Ɠ������Ȃ邱�Ƃ��킩��B [��]
[4]�@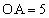 �C
�C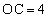 �C
�C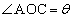 �ł��镽�s�l�ӌ`OABC�ɂ����āA����OA��3�F2�ɓ�������_��D�Ƃ���B�܂��A�_A��ʂ蒼��BD�ɐ����Ȓ����ƒ���OC�̌�_��E�Ƃ���B�������A
�ł��镽�s�l�ӌ`OABC�ɂ����āA����OA��3�F2�ɓ�������_��D�Ƃ���B�܂��A�_A��ʂ蒼��BD�ɐ����Ȓ����ƒ���OC�̌�_��E�Ƃ���B�������A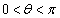 �Ƃ���B
�Ƃ���B
�ȉ��A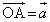 �C
�C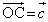 �Ƃ����A����t ��p����
�Ƃ����A����t ��p����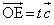 �ƕ\���B
�ƕ\���B
(1) t ��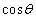 ��p���ĕ\�����B
��p���ĕ\�����B �ƂȂ�̂ŁA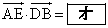 �ɂ��
�ɂ�� 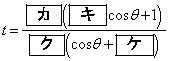 �@����@
�@����@�ƂȂ�B
(2) �_E�͐���OC��ɂ���Ƃ���Bθ �̂Ƃ蓾��l�͈̔͂����߂悤�B�������A����OC�͗��[�̓_O�CC���܂ނ��̂Ƃ���B�ȉ��A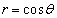 �Ƃ����B
�Ƃ����B �_E������OC��ɂ��邱�Ƃ���A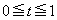 �ł���B
�ł���B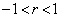 �Ȃ̂ŁA�@�̉E�ӂ�
�Ȃ̂ŁA�@�̉E�ӂ�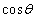 ��r�ɒu������������
��r�ɒu������������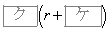 �͐��ł���B���������āA����
�͐��ł���B���������āA����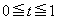 ��
�� 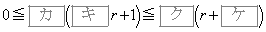 �@����A
�@����A�ƂȂ�B
r�ɂ��Ă̕s�����A���������Ƃɂ��Aθ �̂Ƃ蓾��l�͈̔͂�
�ł��邱�Ƃ��킩��B
(3) 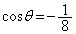 �Ƃ���B����AE�ƒ���BD�̌�_��F�Ƃ��A�O�p�`BEF�̖ʐς����߂悤�B�@�ɂ��A
�Ƃ���B����AE�ƒ���BD�̌�_��F�Ƃ��A�O�p�`BEF�̖ʐς����߂悤�B�@�ɂ��A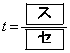 �ƂȂ�
�ƂȂ� �ƂȂ�B���������āA�_F�͐���AE��1�F �ɓ�������B���̂��ƂƁA���s�l�ӌ`OABC�̖ʐς�
�ɓ�������B���̂��ƂƁA���s�l�ӌ`OABC�̖ʐς�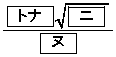 �ł��邱�Ƃ���A�O�p�`BEF�̖ʐς�
�ł��邱�Ƃ���A�O�p�`BEF�̖ʐς�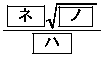 �ł���B
�ł���B [��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 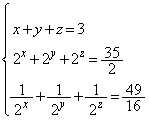
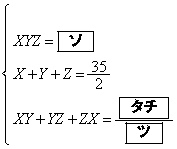
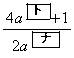 �ł���BC��m�ň͂܂ꂽ�}�`�̖ʐς�T�Ƃ���B
�ł���BC��m�ň͂܂ꂽ�}�`�̖ʐς�T�Ƃ���B �̂Ƃ��ł���A���̂Ƃ��A
�̂Ƃ��ł���A���̂Ƃ��A �ł���B
�ł���B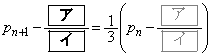 �@(
�@(
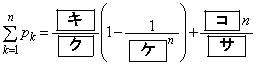
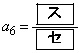 �C
�C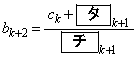 �C
�C
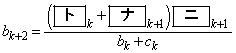
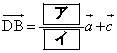 �C
�C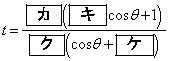 �@����@
�@����@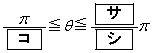
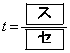 �ƂȂ�
�ƂȂ�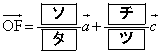
 �ł��邱�Ƃ���A�O�p�`BEF�̖ʐς�
�ł��邱�Ƃ���A�O�p�`BEF�̖ʐς� �ł���B
�ł���B