�@�Z���^�[���wIIB '13�N��1��@
[1]�@O�����_�Ƃ�����W���ʏ��2�_A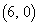 �CB
�CB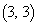 ���Ƃ�A����AB��2�F1�ɓ�������_��P�C1�F2�ɊO������_��Q�Ƃ���B3�_O�CP�CQ��ʂ�~��C�Ƃ���B
���Ƃ�A����AB��2�F1�ɓ�������_��P�C1�F2�ɊO������_��Q�Ƃ���B3�_O�CP�CQ��ʂ�~��C�Ƃ���B (1) P�̍��W��( �C
�C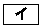 )�ł���AQ�̍��W��(
)�ł���AQ�̍��W��( �C
�C )�ł���B
)�ł���B (2) �~C�̕����������̂悤�ɋ��߂悤�B����OP�̒��_��ʂ�AOP�ɐ����Ȓ����̕�������
�ł���A����PQ�̒��_��ʂ�APQ�ɐ����Ȓ����̕�������
�ł���B
������2�����̌�_���~C�̒��S�ł��邱�Ƃ���A�~C�̕�������
�ł��邱�Ƃ��킩��B
(3) �~C��x���̓�̌�_�̂����A�_O�ƈقȂ��_��R�Ƃ���ƁAR�͐���OA��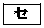 �F1�ɊO������B
�F1�ɊO������B
[2]�@�A��������
(��) 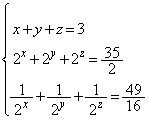
��������x�Cy�Cz�����߂悤�B�������A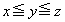 �Ƃ���B
�Ƃ���B
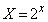 �C
�C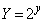 �C
�C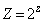 �Ƃ����ƁA
�Ƃ����ƁA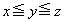 �ɂ��
�ɂ��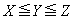 �ł���B(��)����AX�CY�CZ�̊W��
�ł���B(��)����AX�CY�CZ�̊W�� ��������B
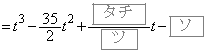
���̊W���𗘗p����ƁAt ��3����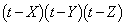 ��
�� �ƂȂ�B���������āA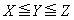 �ɂ��
�ɂ�� �ł��邱�Ƃ��킩��B
���@����1��������܂߁A�Z���^�[�����ł����Ȃ�o��\����ω��������̂͏��߂Ă̂��Ƃł��B��w�n�E���n���̒��ɂ͋������l������Ǝv���܂����A�ӊO�ƕ��ϓ_�͒Ⴍ����܂���ł����B�ȑO�ɂ�����ʼn�������̕��͂��o�邼�ƑO���̂����Ƀl�b�g�\�����ꂽ���Ƃ�����܂������A���O�ɏo��\���ɕω�������ƘR��Ă����̂ł͂Ȃ����Ƌ^�킴��܂���B
[1](1) 2�_A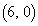 �CB
�CB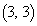 �ɂ��āA����AB��2�F1����������_P�̍��W�́A
�ɂ��āA����AB��2�F1����������_P�̍��W�́A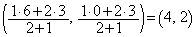
����AB��1�F2�ɊO������_Q�̍��W�́A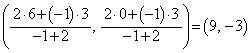 (�A) 4�@(�C) 2�@(�E) 9�@(�G) �|�@(�I) 3 ......[��]
(�A) 4�@(�C) 2�@(�E) 9�@(�G) �|�@(�I) 3 ......[��] (2) ����OP�̒��_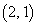 ��ʂ�OP�ɐ����Ȓ����́A�X����
��ʂ�OP�ɐ����Ȓ����́A�X����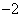 �Ȃ̂ŁA���̕������́A
�Ȃ̂ŁA���̕������́A ����PQ�̒��_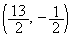 ��ʂ�PQ�ɐ����Ȓ����́A�X����
��ʂ�PQ�ɐ����Ȓ����́A�X����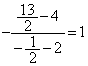 �Ȃ̂ŁA���̕������́A
�Ȃ̂ŁA���̕������́A 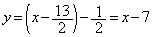 �@����A
�@����A(�J) �|�@(�L) 2�@(�N) 5�@(�P) 7 ......[��]�@�C�A��A������ƁA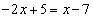 �@��
�@�� 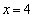 �C
�C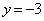
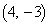 �𒆐S�Ƃ���~C�̕������́A
�𒆐S�Ƃ���~C�̕������́A ���_O��ʂ�̂ŁA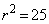 �C����āA
�C����āA (�R) 4�@(�T) 3�@(�V) 2�@(�X) 5 ......[��]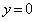 �Ƃ���ƁAx���Ƃ̌�_�́A
�Ƃ���ƁAx���Ƃ̌�_�́A 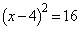 �@��
�@�� 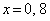
���_O�ƈقȂ�_R�́A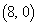 �CR�͐���OA��OR�FRA = 4�F1�ɓ������܂��B(�Z) 4 ......[��]
�CR�͐���OA��OR�FRA = 4�F1�ɓ������܂��B(�Z) 4 ......[��]
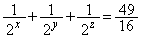 ���A
���A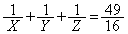 �C����āA
�C����āA�� 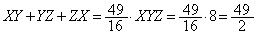
(�\) 8�@(�^) 4�@(�`) 9�@(�c) 2 ......[��] (�e) 1�@(�g) 1�@(�i) 6 ......[��]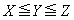 ���A
���A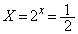 �C
�C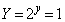 �C
�C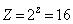
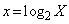 (�ΐ������Q��)�ł����A
(�ΐ������Q��)�ł����A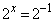 �C
�C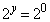 �C
�C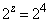 ���A
���A (�j) 2�@(�k) �|�@(�l) 1�@(�m) 0�@(�n) 4 ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 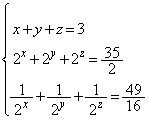
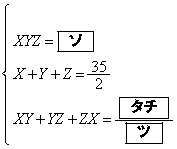
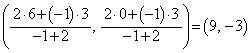
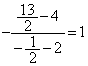 �Ȃ̂ŁA���̕������́A
�Ȃ̂ŁA���̕������́A