センター数学IIB '13年第2問
aを正の実数として、xの関数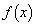 を
を
とする。
関数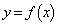 は、
は、 で極大値
で極大値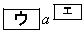 をとり、
をとり、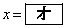 で極小値
で極小値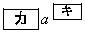 をとる。このとき、2点
をとる。このとき、2点
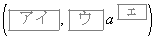 ,
,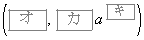
をCとする。原点におけるCの接線 の方程式は
の方程式は
である。また、原点を通り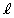 に垂直な直線mの方程式は
に垂直な直線mの方程式は
である。
x軸に関して放物線Cと対称な放物線
をDとする。Dと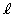 で囲まれた図形の面積Sは
で囲まれた図形の面積Sは
である。
放物線Cと直線mの交点のx座標は、0と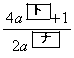 である。Cとmで囲まれた図形の面積をTとする。
である。Cとmで囲まれた図形の面積をTとする。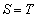 となるのは
となるのは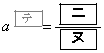 のときであり、このとき、
のときであり、このとき、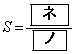 である。
である。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 以前の微積の問題と比べるとかなり計算しやすくなっていますが、面積以降はかなり煩雑です。
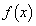 は
は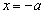 で極大値
で極大値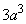 をとり、
をとり、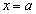 で極小値
で極小値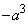 をとる(3次関数の増減を参照)。
をとる(3次関数の増減を参照)。
(ア) − (イ) a (ウ) 3 (エ) 3 (オ) a (オ) − (カ) 3 ......[答]
放物線Cの方程式を、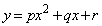 とすると、
とすると、
原点を通るので、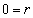
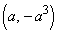 を通るので、
を通るので、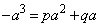
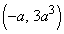 を通るので、
を通るので、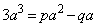
∴ 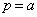 ,
,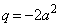
C: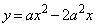
(ク) a (ケ) 2 (コ) 2 ......[答]
原点におけるCの接線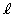 の傾きは、
の傾きは、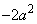
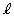 :
: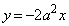
原点を通り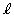 に垂直な直線mの傾きは、
に垂直な直線mの傾きは、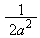
m: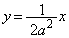
(セ) 2 (ソ) 2 ......[答]
x軸に関して放物線Cと対称な放物線D: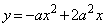
Dと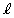 を連立すると、
を連立すると、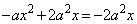 ∴
∴ 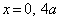
Dと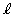 で囲まれた図形の面積Sは、
で囲まれた図形の面積Sは、
(タ) 3 (チ) 2 (ツ) 3 (テ) 4 ......[答]
Cとmを連立すると、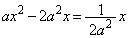 ∴
∴ 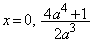
(ト) 4 (ナ) 3 ......[答]
Cとmで囲まれた図形の面積Tは、
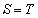 とすると、
とすると、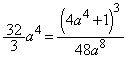 ,
,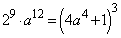 ,
,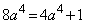 ∴
∴ 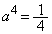
(ニ) 1 (ヌ) 4 (ネ) 8 (ノ) 3 ......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
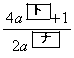 である。Cとmで囲まれた図形の面積をTとする。
である。Cとmで囲まれた図形の面積をTとする。 のときであり、このとき、
のときであり、このとき、 である。
である。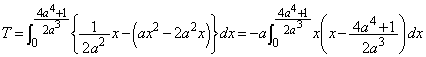
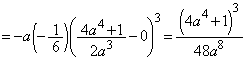
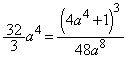 ,
,