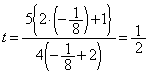�@�Z���^�[���wIIB '13�N��4��@
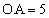 �C
�C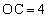 �C
�C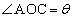 �ł��镽�s�l�ӌ`OABC�ɂ����āA����OA��3�F2�ɓ�������_��D�Ƃ���B�܂��A�_A��ʂ蒼��BD�ɐ����Ȓ����ƒ���OC�̌�_��E�Ƃ���B�������A
�ł��镽�s�l�ӌ`OABC�ɂ����āA����OA��3�F2�ɓ�������_��D�Ƃ���B�܂��A�_A��ʂ蒼��BD�ɐ����Ȓ����ƒ���OC�̌�_��E�Ƃ���B�������A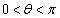 �Ƃ���B
�Ƃ���B
�ȉ��A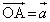 �C
�C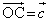 �Ƃ����A����t ��p����
�Ƃ����A����t ��p����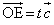 �ƕ\���B
�ƕ\���B
(1) t ��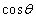 ��p���ĕ\�����B
��p���ĕ\�����B �ƂȂ�̂ŁA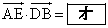 �ɂ��
�ɂ�� 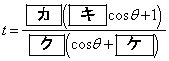 �@����@
�@����@�ƂȂ�B
(2) �_E�͐���OC��ɂ���Ƃ���Bθ �̂Ƃ蓾��l�͈̔͂����߂悤�B�������A����OC�͗��[�̓_O�CC���܂ނ��̂Ƃ���B�ȉ��A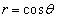 �Ƃ����B
�Ƃ����B �_E������OC��ɂ��邱�Ƃ���A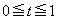 �ł���B
�ł���B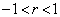 �Ȃ̂ŁA�@�̉E�ӂ�
�Ȃ̂ŁA�@�̉E�ӂ�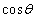 ��r�ɒu������������
��r�ɒu������������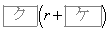 �͐��ł���B���������āA����
�͐��ł���B���������āA����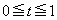 ��
�� 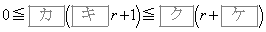 �@����A
�@����A�ƂȂ�B
r�ɂ��Ă̕s�����A���������Ƃɂ��Aθ �̂Ƃ蓾��l�͈̔͂�
�ł��邱�Ƃ��킩��B
(3) 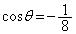 �Ƃ���B����AE�ƒ���BD�̌�_��F�Ƃ��A�O�p�`BEF�̖ʐς����߂悤�B�@�ɂ��A
�Ƃ���B����AE�ƒ���BD�̌�_��F�Ƃ��A�O�p�`BEF�̖ʐς����߂悤�B�@�ɂ��A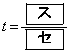 �ƂȂ�
�ƂȂ� �ƂȂ�B���������āA�_F�͐���AE��1�F �ɓ�������B���̂��ƂƁA���s�l�ӌ`OABC�̖ʐς�
�ɓ�������B���̂��ƂƁA���s�l�ӌ`OABC�̖ʐς�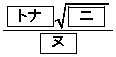 �ł��邱�Ƃ���A�O�p�`BEF�̖ʐς�
�ł��邱�Ƃ���A�O�p�`BEF�̖ʐς�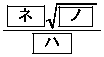 �ł���B
�ł���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���\������N�܂łƕς��A���̖��ŎO�p���������Ă���W������A(3)�̓Z���^�[�����Ƃ��Ă͂���x�������Ȃ��Ă��܂��B
(1) 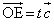 �C
�C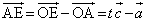 �@����B
�@����B (�A) 2�@(�C) 5 ......[��]
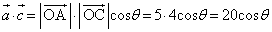 �@����D�@(�������Q��)
�@����D�@(�������Q��)(�E) 2�@(�G) 0 ......[��]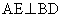 ���A
���A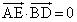 (�I) 0 ......[��]�D��p���āA
(�I) 0 ......[��]�D��p���āA �� 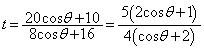 �@����@(�J) 5�@(�L) 2�@(�N) 4�@(�P) 2 ......[��]
�@����@(�J) 5�@(�L) 2�@(�N) 4�@(�P) 2 ......[��]
(2) �A���A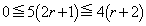
���̕s�������A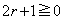 �@��
�@�� 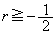 �E�̕s�������A
�E�̕s�������A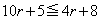 �@��
�@�� 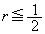 ����āA
����āA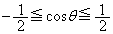 �@��
�@�� 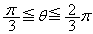 �@(�O�p�����܂ޕs�������Q��)
�@(�O�p�����܂ޕs�������Q��)
(�R) 3�@(�T) 2�@(�V) 3 ......[��]
(3) �@���A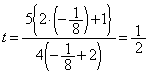
(�X) 1�@(�Z) 2 ......[��]����āA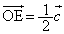 �ƂȂ�AE��OC�̒��_�B
�ƂȂ�AE��OC�̒��_�B
�B��p���āA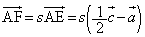 �Ƃ����ƁA
�Ƃ����ƁA 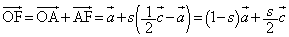 �@����E
�@����E�܂��AF��BD��̓_�Ȃ̂ŁA
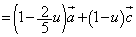 �@����F
�@����F�E�C�F�̌W�����r���āA
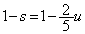 �C
�C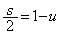
�� 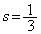 �C
�C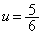
�E���A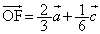 (�\) 2�@(�^) 3�@(�`) 1�@(�c) 6 ......[��]
(�\) 2�@(�^) 3�@(�`) 1�@(�c) 6 ......[��]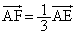 ���AF��AE��1�F2�ɓ�������_�ł��B(�e) 2 ......[��]
���AF��AE��1�F2�ɓ�������_�ł��B(�e) 2 ......[��] ���s�l�ӌ`OABC�̖ʐ�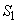 �́A
�́A (�g) 1�@(�i) 5�@(�j) 7�@(�k) 2 ......[��]�O�p�`BEF�̖ʐ�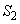 �́A
�́A (�l) 5�@(�m) 7�@(�n) 2 ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 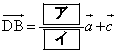 �C
�C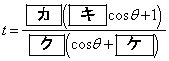 �@����@
�@����@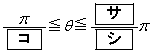
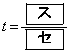 �ƂȂ�
�ƂȂ�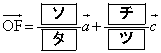
 �ł��邱�Ƃ���A�O�p�`BEF�̖ʐς�
�ł��邱�Ƃ���A�O�p�`BEF�̖ʐς� �ł���B
�ł���B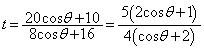 �@����@
�@����@