�@���ʃe�X�g���wIIB '21�N��3��@
[3]�@�ȉ��̖�������ɂ������ẮA�K�v�ɉ����Ė{�▖���̐��K���z�\��p���Ă��悢�B
Q���Z�̍Z���搶�́A������A�V���ō��Z���̓Ǐ��Ɋւ���L����ǂB�����ŁAQ���Z�̐��k�S����ΏۂɁA���O��1�T�Ԃ̓Ǐ����ԂɊւ��āA100�l�̐��k��ׂɒ��o���Ē������s�����B���̌��ʁA100�l�̐��k�̂����A����1�T�ԂɑS���Ǐ������Ȃ��������k��36�l�ł���A100�l�̐��k�̂���1�T�Ԃ̓Ǐ�����(��)�̕��ϒl��204�ł������BQ���Z�̐��k�S���̂���1�T�Ԃ̓Ǐ����Ԃ̕ꕽ�ς�m�C��W������150�Ƃ���B
(1) �S���Ǐ������Ȃ��������k�̕�䗦��0.5�Ƃ���B���̂Ƃ��A100�l�̖���וW�{�̂����őS���Ǐ������Ȃ��������k�̐���\���m���ϐ���X�Ƃ���ƁAX�� �ɏ]���B�܂��AX�̕���(���Ғl)��
�ɏ]���B�܂��AX�̕���(���Ғl)�� �A�W������
�A�W������ �ł���B
�ł���B  �ɂ��ẮA�ł��K���Ȃ��̂��A����
�ɂ��ẮA�ł��K���Ȃ��̂��A���� �`
�` �̂��������I�ׁB
�̂��������I�ׁB �@���K���z
�@���K���z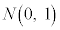 �@�@�@
�@�@�@ �@���z
�@���z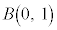
 �@���K���z
�@���K���z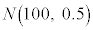 �@�@�@
�@�@�@ �@���z
�@���z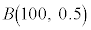
 �@���K���z
�@���K���z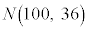 �@�@�@
�@�@�@ �@���z
�@���z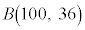
(2) �W�{�̑傫��100�͏\���ɑ傫���̂ŁA100�l�̂����S���Ǐ������Ȃ��������k�̐��͋ߎ��I�ɐ��K���z�ɏ]���B
�S���Ǐ������Ȃ��������k�̕�䗦��0.5�Ƃ���Ƃ��A�S���Ǐ������Ȃ��������k��36�l�ȉ��ƂȂ�m����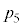 �Ƃ����B
�Ƃ����B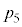 �̋ߎ��l�����߂�ƁA
�̋ߎ��l�����߂�ƁA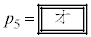 �ł���B
�ł���B
�܂��A�S���Ǐ������Ȃ��������k�̕�䗦��0.4�Ƃ���Ƃ��A�S���Ǐ������Ȃ��������k��36�l�ȉ��ƂȂ�m����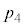 �Ƃ����ƁA
�Ƃ����ƁA �ł���B
�ł���B
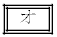 �ɂ��ẮA�ł��K���Ȃ��̂��A����
�ɂ��ẮA�ł��K���Ȃ��̂��A���� �`
�` �̂��������I�ׁB
�̂��������I�ׁB  �@0.001�@�@�@�@
�@0.001�@�@�@�@ �@0.003�@�@�@�@
�@0.003�@�@�@�@ �@0.026
�@0.026 �@0.050�@�@�@�@
�@0.050�@�@�@�@ �@0.133�@�@�@�@
�@0.133�@�@�@�@ �@0.497
�@0.497 �̉Q
�̉Q(3) 1�T�Ԃ̓Ǐ����Ԃ̕ꕽ��m�ɑ���M���x95%�̐M����Ԃ�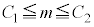 �Ƃ���B�W�{�̑傫��100�͏\���傫�����ƂƁA1�T�Ԃ̓Ǐ����Ԃ̕W�{���ς�204�A��W������150�ł��邱�Ƃ�p����ƁA
�Ƃ���B�W�{�̑傫��100�͏\���傫�����ƂƁA1�T�Ԃ̓Ǐ����Ԃ̕W�{���ς�204�A��W������150�ł��邱�Ƃ�p����ƁA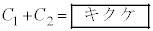 �C
�C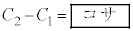 .
. �ł��邱�Ƃ��킩��B
�ł��邱�Ƃ��킩��B �܂��A�ꕽ��m��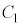 �C
�C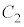 �ɂ��ẮA
�ɂ��ẮA �B
�B
 �̉Q
�̉Q  �@
�@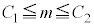 ���K�����藧��
���K�����藧��
 �@
�@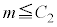 �͕K�����藧���A
�͕K�����藧���A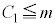 �����藧�Ƃ͌���Ȃ�
�����藧�Ƃ͌���Ȃ�
 �@
�@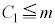 �͕K�����藧���A
�͕K�����藧���A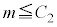 �����藧�Ƃ͌���Ȃ�
�����藧�Ƃ͌���Ȃ�
 �@
�@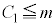 ��
��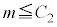 �����藧�Ƃ͌���Ȃ�
�����藧�Ƃ͌���Ȃ�(4) Q���Z�̐}���ψ������A�Z���搶�Ɠ����V���L����ǂ��߁A�Z���搶���������Ă��邱�Ƃ�m�炸�ɁA�}���ψ���Ƃ��čZ���搶�Ɠ��l�̒�����Ǝ��ɍs�����B�������A�������Ԃ͍Z���搶�ɂ�钲���Ɠ������O��1�T�Ԃł���A�Ώۂ�Q���Z�̐��k�S���Ƃ���100�l�̐��k��ׂɒ��o�����B���̒����ɂ�����A�S���Ǐ������Ȃ��������k�̐���n�Ƃ���B
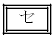
�Z���搶�̒������ʂɂ��ƑS���Ǐ������Ȃ��������k��36�l�ł���A �B
�B
 �̉Q
�̉Q  �@n�͕K��36�ɓ������@�@�@
�@n�͕K��36�ɓ������@�@�@ �@n�͕K��36�����ł���
�@n�͕K��36�����ł���
 �@n�͕K��36���傫���@�@�@
�@n�͕K��36���傫���@�@�@ �@n��36�̑召�͂킩��Ȃ�
�@n��36�̑召�͂킩��Ȃ�(5) (4)�̐}���ψ���s�����������ʂɂ��ꕽ��m�ɑ���M���x95%�̐M����Ԃ�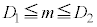 �C�Z���搶���s�����������ʂɂ��ꕽ��m�ɑ���M���x95%�̐M����Ԃ�(3)��
�C�Z���搶���s�����������ʂɂ��ꕽ��m�ɑ���M���x95%�̐M����Ԃ�(3)��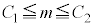 �Ƃ���B�������A��W�c�͓���ł���A1�T�Ԃ̓Ǐ����Ԃ̕�W������150�Ƃ���B
�Ƃ���B�������A��W�c�͓���ł���A1�T�Ԃ̓Ǐ����Ԃ̕�W������150�Ƃ���B ���̂Ƃ��A���� �`
�` �̂����A���������̂�
�̂����A���������̂� ��
�� �ł���B
�ł���B
 �C
�C �̉Q(�̏����͖��Ȃ��B)
�̉Q(�̏����͖��Ȃ��B)  �@
�@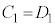 ��
��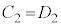 ���K�����藧�B
���K�����藧�B
 �@
�@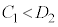 �܂���
�܂���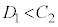 �̂ǂ��炩����݂̂��K�����藧�B
�̂ǂ��炩����݂̂��K�����藧�B
 �@
�@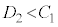 �܂���
�܂���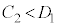 �ƂȂ�ꍇ������B
�ƂȂ�ꍇ������B
 �@
�@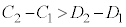 ���K�����藧�B
���K�����藧�B
 �@
�@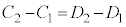 ���K�����藧�B
���K�����藧�B
 �@
�@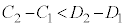 ���K�����藧�B
���K�����藧�B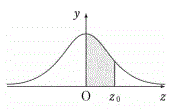
���K���z�\
���̕\�́A�W�����K���z�̕��z�Ȑ��ɂ�����E�}�D�F
�����̖ʐς��܂Ƃ߂����̂ł���B
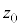 | 0.00 | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 |
| 0.0 | 0.0000 | 0.0040 | 0.0080 | 0.0120 | 0.0160 | 0.0199 | 0.0239 | 0.0279 | 0.0319 | 0.0359 |
| 0.1 | 0.0398 | 0.0438 | 0.0478 | 0.0517 | 0.0557 | 0.0596 | 0.0636 | 0.0675 | 0.0714 | 0.0753 |
| 0.2 | 0.0793 | 0.0832 | 0.0871 | 0.0910 | 0.0948 | 0.0987 | 0.1026 | 0.1064 | 0.1103 | 0.1141 |
| 0.3 | 0.1179 | 0.1217 | 0.1255 | 0.1293 | 0.1331 | 0.1368 | 0.1406 | 0.1443 | 0.1480 | 0.1517 |
| 0.4 | 0.1554 | 0.1591 | 0.1628 | 0.1664 | 0.1700 | 0.1736 | 0.1772 | 0.1808 | 0.1844 | 0.1879 |
| 0.5 | 0.1915 | 0.1950 | 0.1985 | 0.2019 | 0.2054 | 0.2088 | 0.2123 | 0.2157 | 0.2190 | 0.2224 |
| 0.6 | 0.2257 | 0.2291 | 0.2324 | 0.2357 | 0.2389 | 0.2422 | 0.2454 | 0.2486 | 0.2517 | 0.2549 |
| 0.7 | 0.2580 | 0.2611 | 0.2642 | 0.2673 | 0.2704 | 0.2734 | 0.2764 | 0.2794 | 0.2823 | 0.2852 |
| 0.8 | 0.2881 | 0.2910 | 0.2939 | 0.2967 | 0.2995 | 0.3023 | 0.3051 | 0.3078 | 0.3106 | 0.3133 |
| 0.9 | 0.3159 | 0.3186 | 0.3212 | 0.3238 | 0.3264 | 0.3289 | 0.3315 | 0.3340 | 0.3365 | 0.3389 |
| 1.0 | 0.3413 | 0.3438 | 0.3461 | 0.3485 | 0.3508 | 0.3531 | 0.3554 | 0.3577 | 0.3599 | 0.3621 |
| 1.1 | 0.3643 | 0.3665 | 0.3686 | 0.3708 | 0.3729 | 0.3749 | 0.3770 | 0.3790 | 0.3810 | 0.3830 |
| 1.2 | 0.3849 | 0.3869 | 0.3888 | 0.3907 | 0.3925 | 0.3944 | 0.3962 | 0.3980 | 0.3997 | 0.4015 |
| 1.3 | 0.4032 | 0.4049 | 0.4066 | 0.4082 | 0.4099 | 0.4115 | 0.4131 | 0.4147 | 0.4162 | 0.4177 |
| 1.4 | 0.4192 | 0.4207 | 0.4222 | 0.4236 | 0.4251 | 0.4265 | 0.4279 | 0.4292 | 0.4306 | 0.4319 |
| 1.5 | 0.4332 | 0.4345 | 0.4357 | 0.4370 | 0.4382 | 0.4394 | 0.4406 | 0.4418 | 0.4429 | 0.4441 |
| 1.6 | 0.4452 | 0.4463 | 0.4474 | 0.4484 | 0.4495 | 0.4505 | 0.4515 | 0.4525 | 0.4535 | 0.4545 |
| 1.7 | 0.4554 | 0.4564 | 0.4573 | 0.4582 | 0.4591 | 0.4599 | 0.4608 | 0.4616 | 0.4625 | 0.4633 |
| 1.8 | 0.4641 | 0.4649 | 0.4656 | 0.4664 | 0.4671 | 0.4678 | 0.4686 | 0.4693 | 0.4699 | 0.4706 |
| 1.9 | 0.4713 | 0.4719 | 0.4726 | 0.4732 | 0.4738 | 0.4744 | 0.4750 | 0.4756 | 0.4761 | 0.4767 |
| 2.0 | 0.4772 | 0.4778 | 0.4783 | 0.4788 | 0.4793 | 0.4798 | 0.4803 | 0.4808 | 0.4812 | 0.4817 |
| 2.1 | 0.4821 | 0.4826 | 0.4830 | 0.4834 | 0.4838 | 0.4842 | 0.4846 | 0.4850 | 0.4854 | 0.4857 |
| 2.2 | 0.4861 | 0.4864 | 0.4868 | 0.4871 | 0.4875 | 0.4878 | 0.4881 | 0.4884 | 0.4887 | 0.4890 |
| 2.3 | 0.4893 | 0.4896 | 0.4898 | 0.4901 | 0.4904 | 0.4906 | 0.4909 | 0.4911 | 0.4913 | 0.4916 |
| 2.4 | 0.4918 | 0.4920 | 0.4922 | 0.4925 | 0.4927 | 0.4929 | 0.4931 | 0.4932 | 0.4934 | 0.4936 |
| 2.5 | 0.4938 | 0.4940 | 0.4941 | 0.4943 | 0.4945 | 0.4946 | 0.4948 | 0.4949 | 0.4951 | 0.4952 |
| 2.6 | 0.4953 | 0.4955 | 0.4956 | 0.4957 | 0.4959 | 0.4960 | 0.4961 | 0.4962 | 0.4963 | 0.4964 |
| 2.7 | 0.4965 | 0.4966 | 0.4967 | 0.4968 | 0.4969 | 0.4970 | 0.4971 | 0.4972 | 0.4973 | 0.4974 |
| 2.8 | 0.4974 | 0.4975 | 0.4976 | 0.4977 | 0.4977 | 0.4978 | 0.4979 | 0.4979 | 0.4980 | 0.4981 |
| 2.9 | 0.4981 | 0.4982 | 0.4982 | 0.4983 | 0.4984 | 0.4984 | 0.4985 | 0.4985 | 0.4986 | 0.4986 |
| 3.0 | 0.4987 | 0.4987 | 0.4987 | 0.4988 | 0.4988 | 0.4989 | 0.4989 | 0.4989 | 0.4990 | 0.4990 |
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�{�i�I�ȓ��v�̖��ł�(�m�����z�Ɠ��v�I�\�����Q��)�B
(1) �S���Ǐ������Ȃ����k�̊m����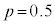 �C
�C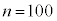 �l�̐��k�𒊏o����̂ŁA�S���Ǐ������Ȃ����k��X�́A���z
�l�̐��k�𒊏o����̂ŁA�S���Ǐ������Ȃ����k��X�́A���z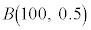 �ɏ]���܂��B
�ɏ]���܂��B �A�@3 ......[��]
X�̕��ς́A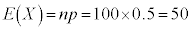
�C�@5�@�E�@0 ......[��]
X�̕W�����́A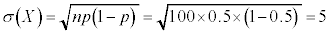
�G�@5 ......[��] (2) �S���Ǐ������Ȃ����k��X�́A����50�C�W����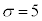 ���A�ߎ��I�����K���z
���A�ߎ��I�����K���z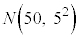 �ɏ]���܂��B
�ɏ]���܂��B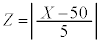 �Ƃ����ƁAZ�͋ߎ��I�ɕW�����K���z
�Ƃ����ƁAZ�͋ߎ��I�ɕW�����K���z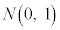 �ɏ]���܂��B
�ɏ]���܂��B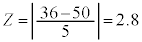 ���A���K���z�\��
���A���K���z�\��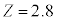 �̂Ƃ���ǂ��0.4974�C�S���Ǐ������Ȃ����k��36�l�ȉ��ƂȂ�m���́A
�̂Ƃ���ǂ��0.4974�C�S���Ǐ������Ȃ����k��36�l�ȉ��ƂȂ�m���́A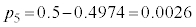 �ŁA���̋ߎ��l��
�ŁA���̋ߎ��l��
�I�@1 ......[��]�Ǐ������Ȃ����k�̕�䗦��0.4�Ƃ���ƁA�ꕽ�ς�40�C�W������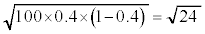 �ɂȂ�̂ŁA
�ɂȂ�̂ŁA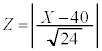 �Ƃ����ƁAZ�͋ߎ��I�ɕW�����K���z
�Ƃ����ƁAZ�͋ߎ��I�ɕW�����K���z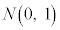 �ɏ]���܂��B���K���z�\��
�ɏ]���܂��B���K���z�\��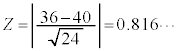 �̂Ƃ����ǂ�łق�0.29���炢�Ȃ̂ŁA
�̂Ƃ����ǂ�łق�0.29���炢�Ȃ̂ŁA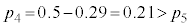 �C����āA
�C����āA
�J�@2 ......[��] (3) �M���x95%�Ƃ����̂́A�m��0.95�Ƃ������ƂŁA���K���z�\�̒l��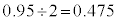 �ɂȂ�Ƃ����
�ɂȂ�Ƃ����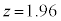 �ł��B��W������150�C�W�{����100�Ȃ̂�(�������Q��)�A
�ł��B��W������150�C�W�{����100�Ȃ̂�(�������Q��)�A ����āA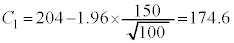 �C
�C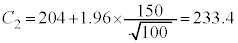
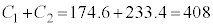
�L�@4�@�N�@0�@�P�@8 ......[��]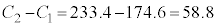 �R�@5�@�T�@8�@�V�@8 ......[��]�M���x95%�Ƃ����̂́A�M���x100%(�@���K�����藧��)�Ɣ�ׂ�5%�����镔��������Ƃ������ƂȂ̂ŁA�K�������@�����藧�킯�ł͂���܂���B�܂�A�ꕽ��m��
�R�@5�@�T�@8�@�V�@8 ......[��]�M���x95%�Ƃ����̂́A�M���x100%(�@���K�����藧��)�Ɣ�ׂ�5%�����镔��������Ƃ������ƂȂ̂ŁA�K�������@�����藧�킯�ł͂���܂���B�܂�A�ꕽ��m��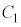 �C
�C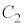 �ɂ��ẮA
�ɂ��ẮA
�X�@3 ......[��] (4) 2�����s�����Ƃ��A�e��łǂ̐��k���W�{�ɑI���̂��A�Ƃ������Ƃɂ��Ă͉��������Ȃ��̂ŁA�S���Ǐ������Ȃ����k���ɂ��Ă����������܂���B�܂�A2��̒����ɂ�����A�S���Ǐ������Ȃ����k���An��36�̑召�͂킩��܂���B(��W�c�ƕW�{���Q��) �Z�@3 ......[��]
(5) �}���ψ���s���������ɂ�����A�Ǐ����Ԃ̕W�{���ς�M�Ƃ���ƁA���肳���ꕽ��m�ɂ���(�������Q��)�A 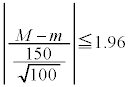 �@��
�@�� 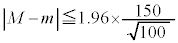
�@�́A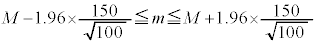
�ƂȂ�A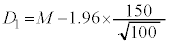 �C
�C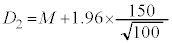 M�̒l�ɂ���āA��������95%�M����Ԃ��d�Ȃ�Ȃ��A�܂�A
M�̒l�ɂ���āA��������95%�M����Ԃ��d�Ȃ�Ȃ��A�܂�A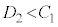 �܂���
�܂���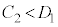 �ƂȂ�ꍇ�����蓾�܂��B�܂��A
�ƂȂ�ꍇ�����蓾�܂��B�܂��A 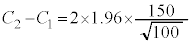 �C
�C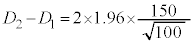
���A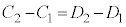 �C�܂�A������W�c�ɑ��ĕW�{�̑傫���������Ȃ�A�M����Ԃ̕��͓������Ȃ�܂��B����āA�������I������
�C�܂�A������W�c�ɑ��ĕW�{�̑傫���������Ȃ�A�M����Ԃ̕��͓������Ȃ�܂��B����āA�������I������ ��
��
�\�@2�@�^�@4 ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 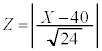 �Ƃ����ƁAZ�͋ߎ��I�ɕW�����K���z
�Ƃ����ƁAZ�͋ߎ��I�ɕW�����K���z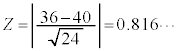 �̂Ƃ����ǂ�łق�0.29���炢�Ȃ̂ŁA
�̂Ƃ����ǂ�łق�0.29���炢�Ȃ̂ŁA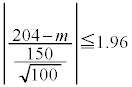 �@��
�@�� 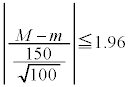 �@��
�@��