�@���ʃe�X�g���wIIB '22�N��1��@
[1]�@���W���ʏ�ɓ_A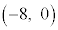 ���Ƃ�B�܂��A�s����
���Ƃ�B�܂��A�s���� �̕\���̈��D�Ƃ���B
(1) �̈�D�́A���S���_ �C���a��
�C���a�� �̉~��
�̉~��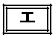 �ł���B
�ł���B 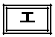 �̉Q
�̉Q
 �@���@�@
�@���@�@ �@�����@�@
�@�����@�@ �@�O��
�@�O��
 �@������ѓ����@�@
�@������ѓ����@�@ �@������ъO��
�@������ъO��
�ȉ��A�_ ��Q�Ƃ��A������
��Q�Ƃ��A�������̕\���}�`��C�Ƃ���B
(2) �_A��ʂ钼���Ɨ̈�D�����L�_�����̂͂ǂ̂悤�ȂƂ������l���悤�B
(i) (1)�ɂ��A����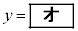 �͓_A��ʂ�C�̐ڐ��̈�ƂȂ邱�Ƃ��킩��B
�͓_A��ʂ�C�̐ڐ��̈�ƂȂ邱�Ƃ��킩��B ���Y����ƉԎq����͓_A��ʂ�C�̂�����̐ڐ��ɂ��Ęb���Ă���B
�_A��ʂ�A�X����k�̒�����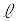 �Ƃ���B
�Ƃ���B
���Y�F����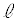 �̕�������
�̕�������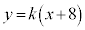 �ƕ\�����Ƃ��ł��邩��A�����
�ƕ\�����Ƃ��ł��邩��A����� �ɑ�����邱�ƂŐڐ������߂�ꂻ�����ˁB
�Ԏq�Fx���ƒ���AQ�̂Ȃ��p�̃^���W�F���g�ɒ��ڂ��邱�Ƃł����߂�ꂻ������B
(ii) ���Y����̋��ߕ��ɂ��čl���Ă݂悤�B
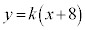 ��
��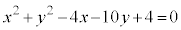 �ɑ������ƁAx�ɂ��Ă�2��������
�ɑ������ƁAx�ɂ��Ă�2����������������B���̕������� �̂Ƃ���k�̒l���ڐ��̌X���ƂȂ�B
�̂Ƃ���k�̒l���ڐ��̌X���ƂȂ�B
 �̉Q
�̉Q
 �@�d��������
�@�d��������
 �@�قȂ��̎������������A���0�ł���
�@�قȂ��̎������������A���0�ł���
 �@�قȂ��̐��̎�����������
�@�قȂ��̐��̎�����������
 �@���̎������ƕ��̎�����������
�@���̎������ƕ��̎�����������
 �@�قȂ��̕��̎�����������
�@�قȂ��̕��̎�����������
 �@�قȂ��̋�����������
�@�قȂ��̋�����������
(iii) �Ԏq����̋��ߕ��ɂ��čl���Ă݂悤�B
x���ƒ���AQ�̂Ȃ��p��θ (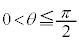 )�Ƃ����
)�Ƃ���� �ł���A����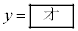 �ƈقȂ�ڐ��̌X����
�ƈقȂ�ڐ��̌X����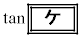 �ƕ\�����Ƃ��ł���B
�ƕ\�����Ƃ��ł���B
 �̉Q
�̉Q
 �@θ�@�@
�@θ�@�@ �@
�@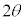 �@�@
�@�@ �@
�@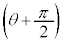
 �@
�@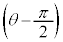 �@�@
�@�@ �@
�@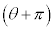 �@�@
�@�@ �@
�@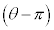
 �@
�@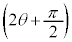 �@�@
�@�@ �@
�@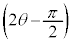
(iv) �_A��ʂ�C�̐ڐ��̂����A����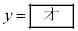 �ƈقȂ�ڐ��̌X����
�ƈقȂ�ڐ��̌X����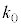 �Ƃ���B���̂Ƃ��A(ii)�܂���(iii)�̍l������p���邱�Ƃɂ��
�Ƃ���B���̂Ƃ��A(ii)�܂���(iii)�̍l������p���邱�Ƃɂ�� �ł��邱�Ƃ��킩��B
���� �Ɨ̈�D�����L�_�����悤��k�̒l�͈̔͂�
�Ɨ̈�D�����L�_�����悤��k�̒l�͈̔͂� �ł���B
�ł���B
 �̉Q
�̉Q
 �@
�@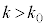 �@�@
�@�@ �@
�@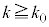
 �@
�@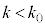 �@�@
�@�@ �@
�@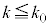
 �@
�@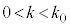 �@�@
�@�@ �@
�@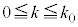
[2]�@a�Cb�͐��̎����ł���A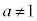 �C
�C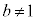 �����Ƃ���B���Y�����
�����Ƃ���B���Y�����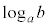 �C
�C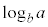 �̑召�W�ׂ邱�Ƃɂ����B
�̑召�W�ׂ邱�Ƃɂ����B
(1) ���Y����͎��̂悤�ȍl�@�������B
�܂��A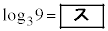 �C
�C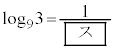 �ł���B���̏ꍇ
�ł���B���̏ꍇ �����藧�B
����A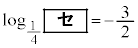 �C
�C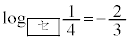 �ł���B���̏ꍇ
�ł���B���̏ꍇ �����藧�B
(2) ������
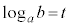 �@����@
�@����@�Ƃ����B
(1)�̍l�@�����Ƃɂ��āA���Y����͎��̎������藧�Ɛ������A���ꂪ���������Ƃ��m���߂邱�Ƃɂ����B
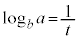 �@����A
�@����A�@�ɂ��A �ł���B���̂��Ƃ��
�ł���B���̂��Ƃ�� �������A�A�����藧���Ƃ��m���߂���B
�������A�A�����藧���Ƃ��m���߂���B
 �̉Q
�̉Q
 �@
�@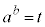 �@�@
�@�@ �@
�@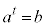 �@�@
�@�@ �@
�@
 �@
�@ �@�@
�@�@ �@
�@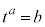 �@�@
�@�@ �@
�@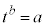
 �̉Q
�̉Q
 �@
�@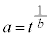 �@�@
�@�@ �@
�@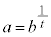 �@�@
�@�@ �@
�@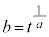
 �@
�@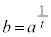 �@�@
�@�@ �@
�@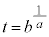 �@�@
�@�@ �@
�@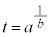
(3) ���ɁA���Y�����(2)�̍l�@�����Ƃɂ���
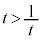 �@����B
�@����B��������t (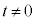 )�̒l�͈̔͂����߂��B
)�̒l�͈̔͂����߂��B
���Y����̍l�@
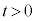 �Ȃ�A�B�̗��ӂ�t ���|���邱�Ƃɂ��A
�Ȃ�A�B�̗��ӂ�t ���|���邱�Ƃɂ��A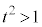 ��B���̂悤��t (
��B���̂悤��t (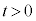 )�̒l�͈̔͂�
)�̒l�͈̔͂�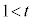 �ł���B
�ł���B
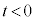 �Ȃ�A�B�̗��ӂ�t ���|���邱�Ƃɂ��A
�Ȃ�A�B�̗��ӂ�t ���|���邱�Ƃɂ��A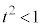 ��B���̂悤��t (
��B���̂悤��t (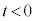 )�̒l�͈̔͂�
)�̒l�͈̔͂�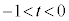 �ł���B
�ł���B���̍l�@�ɂ��A�B����t (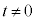 )�̒l�͈̔͂�
)�̒l�͈̔͂� 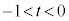 �C
�C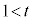
�ł��邱�Ƃ��킩��B
�����ŁAa�̒l�����߂��Ƃ��A�s����
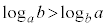 �@����C
�@����C��������b (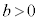 �C
�C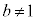 )�̒l�͈̔͂ɂ��čl����B
)�̒l�͈̔͂ɂ��čl����B
�C����b�̒l�͈̔͂́A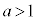 �̂Ƃ���
�̂Ƃ��� �ł���A
�ł���A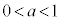 �̂Ƃ���
�̂Ƃ��� �ł���B
�ł���B
 �̉Q
�̉Q
 �@
�@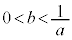 �C
�C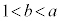 �@�@
�@�@ �@
�@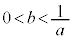 �C
�C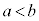
 �@
�@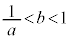 �C
�C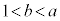 �@�@
�@�@ �@
�@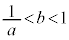 �C
�C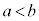
 �̉Q
�̉Q
 �@
�@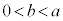 �C
�C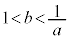 �@�@
�@�@ �@
�@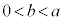 �C
�C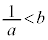
 �@
�@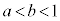 �C
�C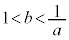 �@�@
�@�@ �@
�@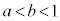 �C
�C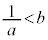
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���wIA�Ƃ̗����Ɉ��R�Ƃ������܂����A���ʃe�X�g�Ƃ��ẮA�{��̕��j������ׂ��p���Ǝv���܂��B
[1]�@�_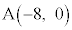
�̈�D�F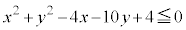
���AD�́A���S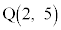 �C���a5�̉~�̎��y�ѓ����ł�(�~�̕��������Q��)�B
�C���a5�̉~�̎��y�ѓ����ł�(�~�̕��������Q��)�B
�A�@2�@�C�@5�@�E�@5�@�G 3 ......[��] C�F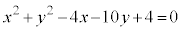 �C
�C �@����D
�@����D (2)(i) ����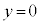 (x��)�͓_A��ʂ�܂��B�~C�̒��S��y���W�Ɣ��a����v����̂ŁA�~C��x���ɐڂ��܂�(�~�ƒ����̈ʒu�W���Q��)�B
(x��)�͓_A��ʂ�܂��B�~C�̒��S��y���W�Ɣ��a����v����̂ŁA�~C��x���ɐڂ��܂�(�~�ƒ����̈ʒu�W���Q��)�B �I�@0 ......[��]
(ii) �_A��ʂ�A�X����k�̒���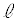 �́A
�́A 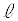 �F
�F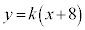
������D�ɑ������ƁA
���̕��������d�������Ƃ���k�̒l���ڐ��̌X���ɂȂ�܂��B
�J�@0 ......[��]
(iii) Q����x���ɉ��낵�������̑�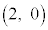 ��R�Ƃ��܂��B
��R�Ƃ��܂��B �L�@1�@�N�@2 ......[��]
A����C�Ɉ�����2�{�̐ڐ��́A����AQ�Ɋւ��đΏ̂Ȃ̂ŁAC�ɐڂ��钼��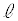 ��x���̂Ȃ��p��
��x���̂Ȃ��p��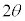 �ŁA���̒���
�ŁA���̒���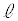 �̌X����
�̌X����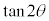 �ł��B
�ł��B
�P�@1 ......[��] (iv) �Ԏq����̍l�����̕������N�ł��B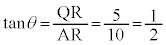 ���A
���A �R�@4�@�T�@3 ......[��]����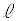 �Ɨ̈�D�����L�_�����悤��k�̒l�͈̔͂�
�Ɨ̈�D�����L�_�����悤��k�̒l�͈̔͂�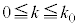
�V�@5 ......[��]
�X�@2 ......[��]
�Z�@8 ......[��]
(2) 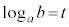 �@����@
�@����@ 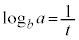 �@����A
�@����A
�@���A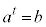 �ŁA
�ŁA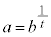 �ł��B
�ł��B
�\�@1�@�^�@1 ......[��](3) 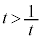 �@����B
�@����B ���Y����̍l�@���A
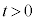 �Ȃ�A
�Ȃ�A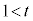
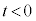 �Ȃ�A
�Ȃ�A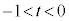
�B����t �͈̔͂́A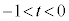 �܂���
�܂��� 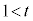 �@����E
�@����E�@���A
�� 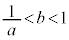 �܂���
�܂��� 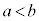 �@����F
�@����F �� 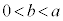 �܂���
�܂��� 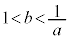 �@����G
�@����G �`�@3�@�c�@0 ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 
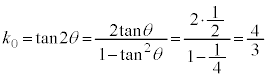
 ���A
���A