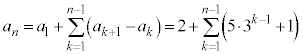�@���ʃe�X�g���wIIB '22�N��4��@
�ȉ��̂悤�ɁA���s�҂Ǝ��]�Ԃ�������o�����Ĉړ��ƒ�~���J��Ԃ��Ă���B���s�҂Ǝ��]�Ԃ̓����ɂ��āA���w�I�ɍl���Ă݂悤�B
��������_�Ƃ��鐔�������l���A���s�҂Ǝ��]�Ԃ����̐���������_�Ƃ݂Ȃ��B��������̓_�̍��W��y�ł���Ƃ��A���̓_�͈ʒuy�ɂ���Ƃ������Ƃɂ���B�܂��A���s�҂�������o�����Ă���x���o�߂������_������x�ƕ\���B���s�҂͎���0�Ɏ�����o�����A���̌����ɖ���1�̑����ŕ����n�߂�B���]�Ԃ͎���2�Ɏ�����o�����A���̌����ɖ���2�̑����ŕ��s�҂�ǂ�������B���]�Ԃ����s�҂ɒǂ����ƁA���s�҂Ǝ��]�Ԃ͂Ƃ���1��������~����B���̌�A���s�҂͍Ăѐ��̌����ɖ���1�̑����ŕ����o���A���]�Ԃ͖���2�̑����Ŏ���ɖ߂�B���]�Ԃ͎���ɓ�������ƁA1��������~������A�Ăі���2�̑����ŕ��s�҂�ǂ�������B������J��Ԃ��A���]�Ԃ͎���ƕ��s�҂̊Ԃ���������B
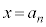 �����]�Ԃ�n��ڂɎ�����o�����鎞���Ƃ��A
�����]�Ԃ�n��ڂɎ�����o�����鎞���Ƃ��A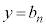 �����̂Ƃ��̕��s�҂̈ʒu�Ƃ���B
�����̂Ƃ��̕��s�҂̈ʒu�Ƃ���B
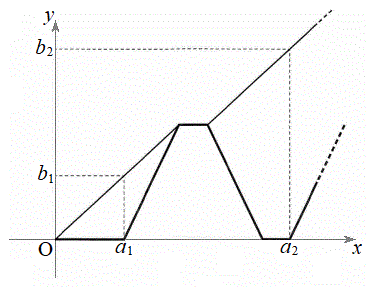 (1) �Ԏq����Ƒ��Y����́A����
(1) �Ԏq����Ƒ��Y����́A����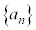 �C
�C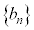 �̈�ʍ������߂邽�߂ɁA���s�҂Ǝ��]�Ԃɂ��āA����x�ɂ����Ĉʒuy�ɂ��邱�Ƃ�O�����_�Ƃ�����W���ʏ�̓_
�̈�ʍ������߂邽�߂ɁA���s�҂Ǝ��]�Ԃɂ��āA����x�ɂ����Ĉʒuy�ɂ��邱�Ƃ�O�����_�Ƃ�����W���ʏ�̓_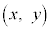 �ŕ\�����Ƃɂ����B
�ŕ\�����Ƃɂ����B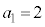 �C
�C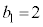 �ɂ��A���]�Ԃ��ŏ��Ɏ�����o������Ƃ��̎����Ǝ��]�Ԃ̈ʒu��\���_�̍��W��
�ɂ��A���]�Ԃ��ŏ��Ɏ�����o������Ƃ��̎����Ǝ��]�Ԃ̈ʒu��\���_�̍��W��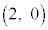 �ł���A���̂Ƃ��̎����ƕ��s�҂̈ʒu��\���_�̍��W��
�ł���A���̂Ƃ��̎����ƕ��s�҂̈ʒu��\���_�̍��W��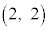 �ł���B�܂��A���]�Ԃ��ŏ��ɕ��s�҂ɒǂ����Ƃ��̎����ƈʒu��\���_�̍��W��
�ł���B�܂��A���]�Ԃ��ŏ��ɕ��s�҂ɒǂ����Ƃ��̎����ƈʒu��\���_�̍��W�� �ł���B�����
�ł���B�����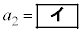 �C
�C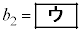
�Ԏq�F����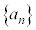 �C
�C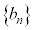 �̈�ʍ��ɂ��čl����O�ɁA
�̈�ʍ��ɂ��čl����O�ɁA �̋��ߕ��ɂ��Đ������Ă݂悤���B
�̋��ߕ��ɂ��Đ������Ă݂悤���B
���Y�F�Ԏq����͂ǂ�����ċ��߂��́B
�Ԏq�F���]�Ԃ����s�҂�ǂ�������Ƃ��ɁA�Ԋu��1���Ԃ�1���k�܂��Ă������Ƃ𗘗p������B
���Y�F���s�҂Ǝ��]�Ԃ̓��������ꂼ�꒼���̕������ŕ\���āA��_���v�Z���ċ��߂邱�Ƃ��ł���ˁB
 ���]�Ԃ�n��ڂɎ�����o������Ƃ��̎����Ǝ��]�Ԃ̈ʒu��\���_�̍��W��
���]�Ԃ�n��ڂɎ�����o������Ƃ��̎����Ǝ��]�Ԃ̈ʒu��\���_�̍��W��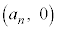 �ł���A���̂Ƃ��̎����ƕ��s�҂̈ʒu��\���_�̍��W��
�ł���A���̂Ƃ��̎����ƕ��s�҂̈ʒu��\���_�̍��W��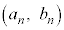 �ł���B����āAn��ڂɎ�����o���������]�Ԃ����ɕ��s�҂ɒǂ����Ƃ��̎����ƈʒu��\���_�̍��W�́A
�ł���B����āAn��ڂɎ�����o���������]�Ԃ����ɕ��s�҂ɒǂ����Ƃ��̎����ƈʒu��\���_�̍��W�́A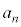 �C
�C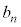 ��p���āA
��p���āA �ƕ\����B
�ƕ\����B
 �C
�C �̉Q(�������̂��J��Ԃ��I��ł��悢�B)
�̉Q(�������̂��J��Ԃ��I��ł��悢�B) �@
�@ �@�@
�@�@ �@
�@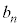 �@�@
�@�@ �@
�@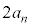
 �@
�@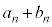 �@�@
�@�@ �@
�@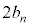 �@�@
�@�@ �@
�@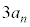
 �@
�@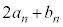 �@�@
�@�@ �@
�@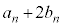 �@�@
�@�@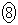 �@
�@
�ȏォ��A����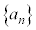 �C
�C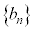 �ɂ��āA���R��n�ɑ��āA�W��
�ɂ��āA���R��n�ɑ��āA�W�� �@����@
�@����@
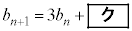 �@����A
�@����A�����藧���Ƃ��킩��B�܂��A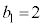 �ƇA����
�ƇA���� 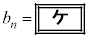 �@(
�@(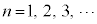 )
)��B���̌��ʂƁA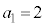 ����ч@����
����ч@���� 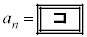 �@(
�@(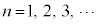 )
)���킩��B
 �C
�C �̉Q(�������̂��J��Ԃ��I��ł��悢�B)
�̉Q(�������̂��J��Ԃ��I��ł��悢�B) �@
�@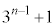 �@�@
�@�@ �@
�@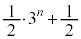
 �@
�@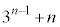 �@�@
�@�@ �@
�@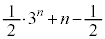
 �@
�@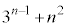 �@�@
�@�@ �@
�@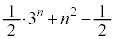
 �@
�@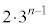 �@�@
�@�@ �@
�@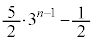
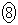 �@
�@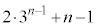 �@�@
�@�@ �@
�@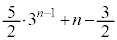
 �@
�@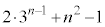 �@�@
�@�@ �@
�@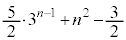
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�v�Z�̂�₱���������x���̘A���Q�����̖��ł��B��蕶��������������̂ŁA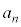 �C
�C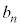 �������w���Ă��邩�A(2)�ʼn�������Ηǂ����A��蕶�̓lj�͂���ł��B�P�ƃR�́A
�������w���Ă��邩�A(2)�ʼn�������Ηǂ����A��蕶�̓lj�͂���ł��B�P�ƃR�́A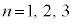 �Ȃǂ�������1���̐��������߂�A�Ƃ������������ł��Ȃ��悤�ɁAn�̎���I������`���ɂȂ��Ă��āA�o��@�̍H�v�������܂��B
�Ȃǂ�������1���̐��������߂�A�Ƃ������������ł��Ȃ��悤�ɁAn�̎���I������`���ɂȂ��Ă��āA�o��@�̍H�v�������܂��B
1��ڂɎ��]�Ԃ��o������͎̂���2�Ȃ̂ŁA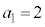 �C���̂Ƃ��ɕ��s�҂͋���2�i��ł���̂ŁA
�C���̂Ƃ��ɕ��s�҂͋���2�i��ł���̂ŁA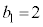 �ł��B
�ł��B
(1) ���s�҂Ǝ��]�Ԃ̋���2�𑬂��̍�1�Œǂ�������̂ŁA
����2�ɏo���������]�Ԃ��ǂ���������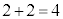 �C�����ƈʒu��\���_�̍��W��
�C�����ƈʒu��\���_�̍��W��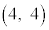 �ł��B
�ł��B
�A�@4 ......[��]����5�Ɏ��]�Ԃ��A����4�𑬂�2�Ŏ���ɖ߂��Ď���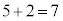 �Ɏ���ɒ����A����8�ɏo������̂ŁA
�Ɏ���ɒ����A����8�ɏo������̂ŁA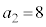 �C���s�҂͎���5���瑬��1�Ői�ނƎ���8�ɂ�
�C���s�҂͎���5���瑬��1�Ői�ނƎ���8�ɂ�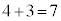 �ɗ���̂ŁA
�ɗ���̂ŁA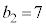
�C�@8�@�E�@7 ......[��]�Ȍ�A�Ԏq�������A���Q���������܂��B
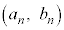 ����l���āA���s�҂Ǝ��]�Ԃ̋���
����l���āA���s�҂Ǝ��]�Ԃ̋���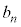 �𑬂��̍�1�Œǂ�������̂ŁA�ǂ����܂ł�
�𑬂��̍�1�Œǂ�������̂ŁA�ǂ����܂ł�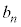 ��������A�ǂ���������
��������A�ǂ���������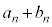 �C���̊ԕ��s�҂�
�C���̊ԕ��s�҂�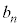 ����
����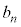 �i�ނ̂ŁA�ǂ����ʒu�́A
�i�ނ̂ŁA�ǂ����ʒu�́A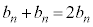 �C�����ƈʒu��\���_�̍��W��
�C�����ƈʒu��\���_�̍��W��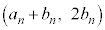 �ł��B
�ł��B
�G�@3�@�I�@4 ......[��]�ǂ�������A���]�Ԃ́A����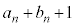 �Ɏ���Ɍ������ďo�����A����
�Ɏ���Ɍ������ďo�����A����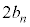 �𑬂�2�Ői�݁A����
�𑬂�2�Ői�݁A����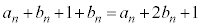 �Ɏ���ɒ����A����
�Ɏ���ɒ����A����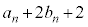 �ɏo������̂ŁA
�ɏo������̂ŁA 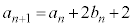 �@����@
�@����@�J�@2�@�L�@2 ......[��]���s�҂͎���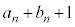 ���瑬��1�Ői�ނƎ���
���瑬��1�Ői�ނƎ���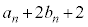 �ɂ́A
�ɂ́A 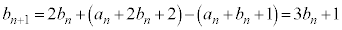 �@����A
�@����A�ɗ��܂�(2���ԑQ�������Q��)�B
�N�@1 ......[��]�A�ŁA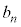 �C
�C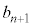 ��α�Œu��������ƁA
��α�Œu��������ƁA 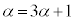 �@����B�@��
�@����B�@�� 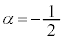
�A�|�B���A
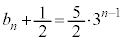 �@��
�@�� 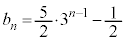
�P�@7 ......[��]
�@�ɑ������ƁA
�R�@9 ......[��]
(2) �G�I���An��ڂɎ��]�Ԃ��ǂ����ʒu��300�����Ȃ̂ŁA
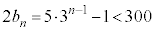 �@��
�@�� 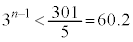
����āA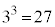 �C
�C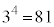 ���
���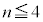 �ƂȂ�A�ʒu300�����ɓ�������܂łɎ��]�Ԃ����s�҂ɒǂ�����4��ł��B
�ƂȂ�A�ʒu300�����ɓ�������܂łɎ��]�Ԃ����s�҂ɒǂ�����4��ł��B
�T�@4 ......[��]�G�I���A4��ڂɎ��]�Ԃ����s�҂ɒǂ��������́A �V�X�Z�@137 ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B