�@���ʃe�X�g���wIIB '23�N��1��@
[1]�@�O�p���̒l�̑召�W�ɂ��čl���悤�B
 �C
�C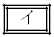 �̉Q(�������̂��J��Ԃ��I��ł��悢�B)
�̉Q(�������̂��J��Ԃ��I��ł��悢�B)
(2) 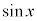 ��
��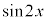 �̒l�̑召�W���ڂ������ׂ悤�B
�̒l�̑召�W���ڂ������ׂ悤�B �ł��邩��A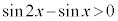 �����藧���Ƃ�
�����藧���Ƃ� �u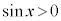 �@���@
�@���@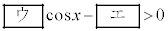 �v�@����@
�v�@����@ �܂���
�u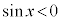 �@���@
�@���@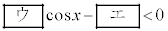 �v�@����A
�v�@����A �����藧���ƂƓ��l�ł���B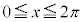 �̂Ƃ��A�@�����藧�悤��x�̒l�͈̔͂�
�̂Ƃ��A�@�����藧�悤��x�̒l�͈̔͂� �ł���A�A�����藧�悤��x�̒l�͈̔͂�
�ł���B����āA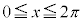 �̂Ƃ��A
�̂Ƃ��A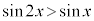 �����藧�悤��x�̒l�͈̔͂�
�����藧�悤��x�̒l�͈̔͂� 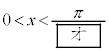 �C
�C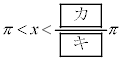
�ł���B
(3) 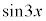 ��
��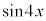 �̒l�̑召�W�ׂ悤�B
�̒l�̑召�W�ׂ悤�B �O�p���̉��@�藝��p����ƁA����
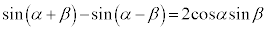 �@����B
�@����B��������B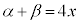 �C
�C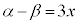 ����α�Cβ�ɑ��ćB��p���邱�Ƃɂ��A
����α�Cβ�ɑ��ćB��p���邱�Ƃɂ��A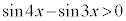 �����藧���Ƃ�
�����藧���Ƃ� �u �@���@
�@���@ �v�@����C
�v�@����C �܂���
�u �@���@
�@���@ �v�@����D
�v�@����D �����藧���ƂƓ��l�ł��邱�Ƃ��킩��B
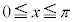 �̂Ƃ��A�C�C�D�ɂ��A
�̂Ƃ��A�C�C�D�ɂ��A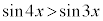 �����藧�悤��x�̒l�͈̔͂�
�����藧�悤��x�̒l�͈̔͂� 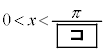 �C
�C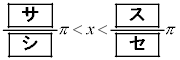
�ł���B
 �C
�C �̉Q(�������̂��J��Ԃ��I��ł��悢�B)
�̉Q(�������̂��J��Ԃ��I��ł��悢�B)  �@0�@�@
�@0�@�@ �@x�@�@
�@x�@�@ �@
�@ �@�@
�@�@ �@
�@
 �@
�@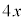 �@�@
�@�@ �@
�@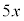 �@�@
�@�@ �@
�@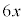 �@
�@ �@
�@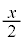
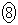 �@
�@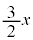 �@�@
�@�@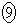 �@
�@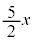 �@�@
�@�@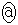 �@
�@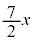 �@�@
�@�@ �@
�@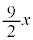
(4) (2)�C(3)�̍l�@����A �̂Ƃ��A
�̂Ƃ��A �����藧�悤��x�̒l�͈̔͂�
�����藧�悤��x�̒l�͈̔͂� 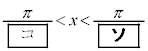 �C
�C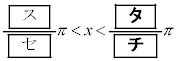
�ł��邱�Ƃ��킩��B
[2](1) 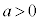 �C
�C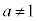 �C
�C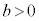 �̂Ƃ��A
�̂Ƃ��A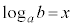 �Ƃ����ƁA
�Ƃ����ƁA �����藧�B
�����藧�B  �̉Q
�̉Q
(2) �l�X�ȑΐ��̒l���L���������������ɂ��čl���悤�B
(i) 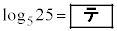 �C
�C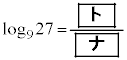 �ł���A�ǂ�����L�����ł���B
�ł���A�ǂ�����L�����ł���B
(ii) 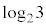 ���L�����Ɩ������̂ǂ���ł��邩���l���悤�B
���L�����Ɩ������̂ǂ���ł��邩���l���悤�B 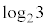 ���L�����ł���Ɖ��肷��ƁA
���L�����ł���Ɖ��肷��ƁA �ł���̂ŁA��̎��R��p�Cq��p����
�ł���̂ŁA��̎��R��p�Cq��p����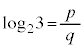 �ƕ\�����Ƃ��ł���B���̂Ƃ��A(1)�ɂ��
�ƕ\�����Ƃ��ł���B���̂Ƃ��A(1)�ɂ��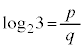 ��
�� �ƕό`�ł���B���܁A2�͋����ł���3�͊�ł���̂ŁA
�ƕό`�ł���B���܁A2�͋����ł���3�͊�ł���̂ŁA �������R��p�Cq�͑��݂��Ȃ��B
�������R��p�Cq�͑��݂��Ȃ��B
���������āA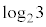 �͖��������Ƃ킩��B
�͖��������Ƃ킩��B
(iii) a�Cb��2�ȏ�̎��R���Ƃ���Ƃ��A(ii)�Ɠ��l�ɍl����ƁA�u �Ȃ��
�Ȃ��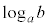 �͂˂ɖ������ł���v���Ƃ��킩��B
�͂˂ɖ������ł���v���Ƃ��킩��B  �̉Q
�̉Q �@
�@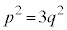 �@�@
�@�@ �@
�@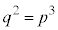 �@�@
�@�@ �@
�@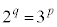
 �@
�@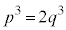 �@�@
�@�@ �@
�@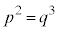 �@�@
�@�@ �@
�@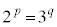
 �̉Q
�̉Q �@a������
�@a������
 �@b������
�@b������
 �@a���
�@a���
 �@b���
�@b���
 �@a��b���Ƃ��ɋ����A�܂���a��b���Ƃ��Ɋ
�@a��b���Ƃ��ɋ����A�܂���a��b���Ƃ��Ɋ
 �@a��b�̂����ꂩ����������ŁA����������
�@a��b�̂����ꂩ����������ŁA����������
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@��N�̑�1��Ɠ��l�A��b�w�͂����鋤�ʃe�X�g�Ƃ��ẮA�{��̕��j������ׂ��p���Ǝv���܂��B
[1](1) 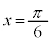 �̂Ƃ��A
�̂Ƃ��A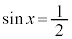 �C
�C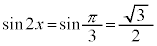 ���(�O�p�����Q��)�A
���(�O�p�����Q��)�A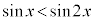 �@�A 0 ......[��]
�@�A 0 ......[��] 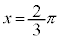 �̂Ƃ��A
�̂Ƃ��A �C
�C ���A
���A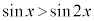 �@�C 2 ......[��]
�@�C 2 ......[��]
 �̂Ƃ��A
�̂Ƃ��A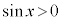 ���
���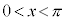 �C
�C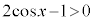 ���
���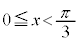 �܂���
�܂���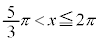 (�O�p�����܂ޕ������E�s�������Q��)�C����āA
(�O�p�����܂ޕ������E�s�������Q��)�C����āA �@�I 3 ......[��]
�@�I 3 ......[��]
�A�����藧�Ȃ�A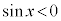 ���
���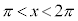 �C
�C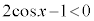 ���
���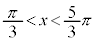 �C����āA
�C����āA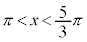 �@�J 5�@�L 3 ......[��]�܂�A
�@�J 5�@�L 3 ......[��]�܂�A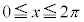 �̂Ƃ�
�̂Ƃ�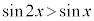 �����藧��x�͈̔͂́A
�����藧��x�͈̔͂́A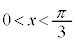 �C
�C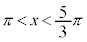 �@����E
�@����E
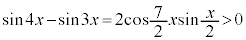 �����藧���Ƃ́A
�����藧���Ƃ́A
�u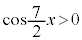 �@���@
�@���@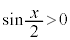 �v�@����C
�v�@����C�N a�@�P 7 ......[��]
�܂��́A
�u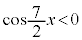 �@���@
�@���@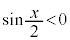 �v�@����D
�v�@����D �����藧���ƂƓ��l�ł��B
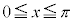 �̂Ƃ��A
�̂Ƃ��A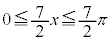 �C
�C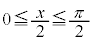
�C���A�u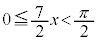 �C
�C �v����
�v���� �@��
�@�� 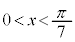 �C
�C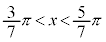
�D�ł�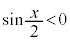 ���s�����B
���s�����B
����āA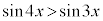 �ƂȂ�x�͈̔͂́A
�ƂȂ�x�͈̔͂́A 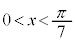 �C
�C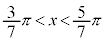 �@����F
�@����F�R 7�@�T 3�@�V 7�@�X 5�@�Z 7 ......[��]
(4) 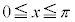 �̂Ƃ��A�F���A
�̂Ƃ��A�F���A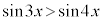 �ƂȂ�̂́A
�ƂȂ�̂́A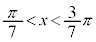 �C
�C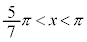 (
(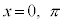 �̂Ƃ��A
�̂Ƃ��A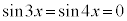 )
)  �ƂȂ�̂́A�E�𗘗p���āA
�ƂȂ�̂́A�E�𗘗p���āA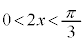 �C
�C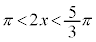 �@��
�@�� 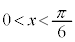 �C
�C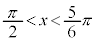
����āA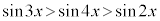 �����藧�悤��x�͈̔͂́A
�����藧�悤��x�͈̔͂́A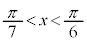 �C
�C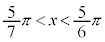
�\ 6�@�^ 5�@�` 6 ......[��]
[2](1) 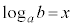 ��
�� 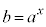 (�ΐ������Q��)�@�c 2 ......[��]
(�ΐ������Q��)�@�c 2 ......[��]
(2)(i) 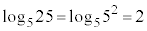 �@�e 2 ......[��]
�@�e 2 ......[��] 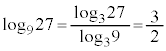 �@�g 3�@�i 2 ......[��]
�@�g 3�@�i 2 ......[��]
(ii) ���R��p�Cq��p���āA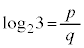 �Ƃ����ƁA
�Ƃ����ƁA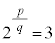
���ӂ�q�悵�āA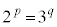 �@�j 5 ......[��]
�@�j 5 ......[��]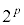 �͋����ŁA
�͋����ŁA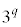 �͊�Ȃ̂ŁA���҂��������Ȃ邱�Ƃ͂Ȃ��A
�͊�Ȃ̂ŁA���҂��������Ȃ邱�Ƃ͂Ȃ��A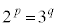 ���������Ȃ��̂ŁA
���������Ȃ��̂ŁA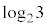 �͗L�����ł͂Ȃ��A�������ł�(�������Q��)�B
�͗L�����ł͂Ȃ��A�������ł�(�������Q��)�B
���l�ɁA���R��p�Cq��p���āA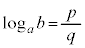 �Ƃ����ƁA
�Ƃ����ƁA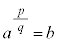
���ӂ�q�悵�āA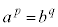 a�Cb�̋��قȂ鎞�A���̓����͐��������A
a�Cb�̋��قȂ鎞�A���̓����͐��������A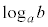 �͖������ł��B�@�k 5 ......[��]
�͖������ł��B�@�k 5 ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 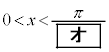
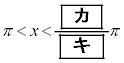
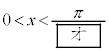 �C
�C
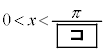 �C
�C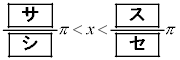
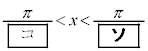 �C
�C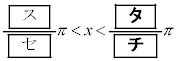
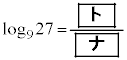 �ł���A�ǂ�����L�����ł���B
�ł���A�ǂ�����L�����ł���B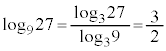 �@�g 3�@�i 2 ......[��]
�@�g 3�@�i 2 ......[��]