�@���ʃe�X�g���wIIB '23�N��2��@
[1](1) k�𐳂̒萔�Ƃ��A����3�������l����B
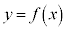 �̃O���t��x���Ƃ̋��L�_�̍��W��
�̃O���t��x���Ƃ̋��L�_�̍��W��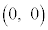 ��
�� �ł���B
�ł���B
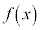 �̓���
�̓���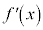 ��
���ł���B
 �̂Ƃ��A
�̂Ƃ��A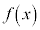 �͋ɏ��l
�͋ɏ��l ���Ƃ�B
���Ƃ�B
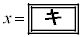 �̂Ƃ��A
�̂Ƃ��A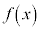 �͋ɑ�l
�͋ɑ�l ���Ƃ�B
���Ƃ�B
�܂��A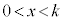 �͈̔͂ɂ�����
�͈̔͂ɂ�����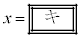 �̂Ƃ�
�̂Ƃ�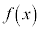 �͍ő�ƂȂ邱�Ƃ��킩��B
�͍ő�ƂȂ邱�Ƃ��킩��B
 �C
�C �`
�` �̉Q(�������̂��J��Ԃ��I��ł��悢�B)
�̉Q(�������̂��J��Ԃ��I��ł��悢�B)  �@0�@�@
�@0�@�@ �@
�@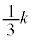 �@�@
�@�@ �@
�@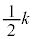 �@�@
�@�@ �@
�@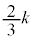
 �@k�@�@
�@k�@�@ �@
�@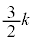 �@�@
�@�@ �@
�@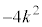 �@�@
�@�@ �@
�@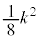
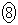 �@
�@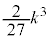 �@�@
�@�@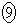 �@
�@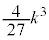 �@�@
�@�@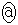 �@
�@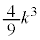 �@�@
�@�@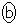 �@
�@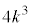
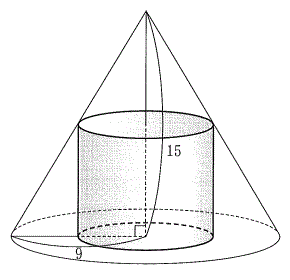 (2) �E�̐}�̂悤�ɒ�ʂ����a9�̉~�ō�����15�̉~���ɓ��ڂ���~�����l����B�~���̒�ʂ̔��a�Ƒ̐ς����ꂼ��x�CV�Ƃ���BV��x�̎��ŕ\����
(2) �E�̐}�̂悤�ɒ�ʂ����a9�̉~�ō�����15�̉~���ɓ��ڂ���~�����l����B�~���̒�ʂ̔��a�Ƒ̐ς����ꂼ��x�CV�Ƃ���BV��x�̎��ŕ\����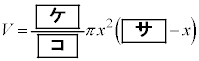 �@(
�@(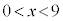 )
)�ł���B(1)�̍l�@���A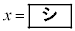 �̂Ƃ�V�͍ő�ƂȂ邱�Ƃ��킩��BV�̍ő�l��
�̂Ƃ�V�͍ő�ƂȂ邱�Ƃ��킩��BV�̍ő�l�� �ł���B
�ł���B
[2](1) ��ϕ�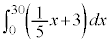 �̒l��
�̒l�� �ł���B
�ł���B �܂��A��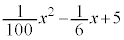 �̕s��ϕ���
�̕s��ϕ��� �ł���B�������AC�͐ϕ��萔�Ƃ���B
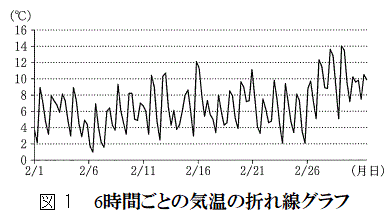 (2) ����n��ł́A���N3�����u�\���C���V�m(���̎��)�̊J�ԗ\�z���v���b��ɂȂ�B���Y����ƉԎq����́A�J�ԓ�����\�z������@�̈�ɁA2���ɓ����Ă���̋C�������Ԃ̊��Ƃ݂āA���̊���ϕ������l�����Ƃɂ�����@�����邱�Ƃ�m�����B�\���C���V�m�̊J�ԓ�����\�z���邽�߂ɁA��l�͐}1��6���Ԗ��̋C���̐܂�������Ȃ���A���̂悤�ɍl���邱�Ƃɂ����B
(2) ����n��ł́A���N3�����u�\���C���V�m(���̎��)�̊J�ԗ\�z���v���b��ɂȂ�B���Y����ƉԎq����́A�J�ԓ�����\�z������@�̈�ɁA2���ɓ����Ă���̋C�������Ԃ̊��Ƃ݂āA���̊���ϕ������l�����Ƃɂ�����@�����邱�Ƃ�m�����B�\���C���V�m�̊J�ԓ�����\�z���邽�߂ɁA��l�͐}1��6���Ԗ��̋C���̐܂�������Ȃ���A���̂悤�ɍl���邱�Ƃɂ����Bx�̒l�͈̔͂�0�ȏ�̎����S�̂Ƃ��āA2��1���ߑO0������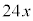 ���Ԍo�������_��x����Ƃ���B(�Ⴆ�A10.3�����2��11���ߑO7��12����\���B)�܂��Ax����̋C����y���Ƃ���B���̂Ƃ��Ay��x�̊��ł���A�����
���Ԍo�������_��x����Ƃ���B(�Ⴆ�A10.3�����2��11���ߑO7��12����\���B)�܂��Ax����̋C����y���Ƃ���B���̂Ƃ��Ay��x�̊��ł���A�����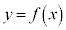 �Ƃ����B�������Ay�͕��ɂ͂Ȃ�Ȃ����̂Ƃ���B
�Ƃ����B�������Ay�͕��ɂ͂Ȃ�Ȃ����̂Ƃ���B
�C����\����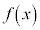 ��p���ē�l�̓\���C���V�m�̊J�ԓ����������ݒ��ōl���邱�Ƃɂ����B
��p���ē�l�̓\���C���V�m�̊J�ԓ����������ݒ��ōl���邱�Ƃɂ����B
�|�ݒ��|�|�|�|�|�|�|�|�|�|�|�|�|
���̎���t �ɑ��āA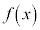 ��0����t �܂Őϕ������l��
��0����t �܂Őϕ������l��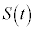 �Ƃ���B���Ȃ킿�A
�Ƃ���B���Ȃ킿�A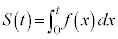 �Ƃ���B����
�Ƃ���B����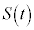 ��400�ɓ��B�����Ƃ��A�\���C���V�m���J�Ԃ���B
��400�ɓ��B�����Ƃ��A�\���C���V�m���J�Ԃ���B
�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|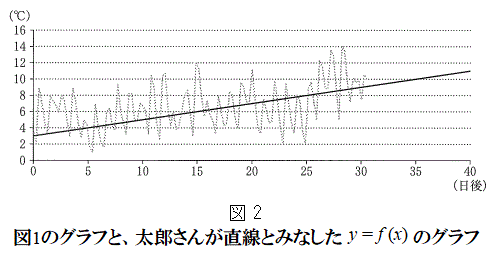 �ݒ��̂��ƁA���Y����͋C����\����
�ݒ��̂��ƁA���Y����͋C����\����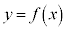 �̃O���t��}2�̂悤�ɒ����Ƃ݂Ȃ��ă\���C���V�m�̊J�ԓ������l���邱�Ƃɂ����B
�̃O���t��}2�̂悤�ɒ����Ƃ݂Ȃ��ă\���C���V�m�̊J�ԓ������l���邱�Ƃɂ����B (i) ���Y����́A
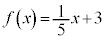 �@(
�@(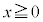 )
)�Ƃ��čl�����B���̂Ƃ��A�\���C���V�m�̊J�ԓ�����2���ɓ����Ă��� �ƂȂ�B
�ƂȂ�B
 �̉Q
�̉Q  �@30����@�@
�@30����@�@ �@35����@�@
�@35����@�@ �@40����
�@40����
 �@45����@�@
�@45����@�@ �@50����@�@
�@50����@�@ �@55����
�@55����
 �@60����@�@
�@60����@�@ �@65����
�@65����
(ii) ���Y����ƉԎq����́A2���ɓ����Ă���30����ȍ~�̋C���ɂ��Ęb�����Ă���B
�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|
���Y�F1������p���ă\���C���V�m�̊J�ԓ��������߂Ă݂���B
�Ԏq�F�C���̏オ�������l���āA2���ɓ����Ă���30����ȍ~�̋C����\������2�����̏ꍇ���l���Ă݂悤���B
�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|
�Ԏq����͋C����\����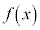 ���A
���A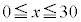 �̂Ƃ��͑��Y����Ɠ����悤��
�̂Ƃ��͑��Y����Ɠ����悤�� �Ƃ��A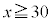 �̂Ƃ���
�̂Ƃ��� �Ƃ��čl�����B�Ȃ��A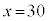 �̂Ƃ��@�̉E�ӂ̒l�ƇA�̉E�ӂ̒l�͈�v����B�Ԏq����̍l��������p���āA�\���C���V�m�̊J�ԓ������l���悤�B(1)���
�̂Ƃ��@�̉E�ӂ̒l�ƇA�̉E�ӂ̒l�͈�v����B�Ԏq����̍l��������p���āA�\���C���V�m�̊J�ԓ������l���悤�B(1)��� �ł���A
�ƂȂ邱�Ƃ��킩��B
�܂��A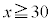 �͈̔͂ɂ�����
�͈̔͂ɂ�����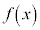 �͑�������B�����
�͑�������B����� �ł��邱�Ƃ��킩��B�ȏ���A�\���C���V�m�̊J�ԓ�����2���ɓ����Ă��� �ƂȂ�B
�ƂȂ�B
 �̉Q
�̉Q  �̉Q
�̉Q �@30������O
�@30������O
 �@30����
�@30����
 �@30�������A����40������O
�@30�������A����40������O
 �@40����
�@40����
 �@40�������A����50������O
�@40�������A����50������O
 �@50����
�@50����
 �@50�������A����60������O
�@50�������A����60������O
 �@60����
�@60����
 �@60�������
�@60�������
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@��{���ł����A��1�⓯�l�ɁA�o��҂̈Ӑ}���悭�c�����Ė��ʂȌv�Z�����Ȃ��悤�ɉ���K�v������܂��B
[1](1) 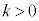 �C
�C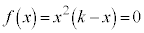 �Ƃ���ƁA
�Ƃ���ƁA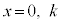 �C
�C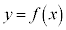 �̃O���t��x���Ƃ̋��L�_�̍��W�́A
�̃O���t��x���Ƃ̋��L�_�̍��W�́A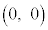 ��
��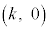 �@�A 4 ......[��]
�@�A 4 ......[��] 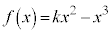 �����������ƁA
�����������ƁA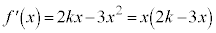 �@�C�E
�@�C�E 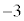 �@�G 2 ......[��]
�@�G 2 ......[��]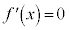 �Ƃ���ƁA
�Ƃ���ƁA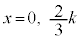 �C
�C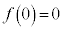 �C
�C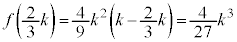 �C�����\�͈ȉ��̂悤�ɂȂ�܂��B
�C�����\�͈ȉ��̂悤�ɂȂ�܂��B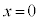 �̂Ƃ��A
�̂Ƃ��A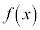 �͋ɏ��l0���Ƃ�܂��B�@�I 0�@�J 0 ......[��]
�͋ɏ��l0���Ƃ�܂��B�@�I 0�@�J 0 ......[��]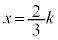 �̂Ƃ��A
�̂Ƃ��A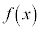 �͋ɑ�l
�͋ɑ�l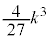 ���Ƃ�܂��B�@�L 3�@�N 9 ......[��]
���Ƃ�܂��B�@�L 3�@�N 9 ......[��]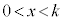 �͈̔͂ɂ����āA
�͈̔͂ɂ����āA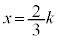 �̂Ƃ�
�̂Ƃ�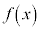 ���ő�l
���ő�l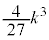 ���Ƃ邱�Ƃ��킩��܂�(3�����̍ő�E�ŏ����Q��)�B�@���(��)
���Ƃ邱�Ƃ��킩��܂�(3�����̍ő�E�ŏ����Q��)�B�@���(��)
(2) �~���̍�����h�Ƃ���ƁA�~���̒��_�ƒ�ʂ̉~�̒��a���܂ޒf�ʂɂ�����O�p�`�̑������A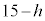 �F15 = x�F9�@��
�F15 = x�F9�@�� 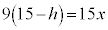 �C
�C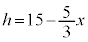
�~���̑̐ς́A
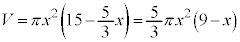 �@�P 5�@�R 3�@�T 9 ......[��]
�@�P 5�@�R 3�@�T 9 ......[��](1)��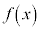 �ƌ���ׂāA
�ƌ���ׂāA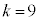 �Ƃ���ƁA(��)���A
�Ƃ���ƁA(��)���A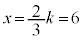 �̂Ƃ�V�͍ő�ɂȂ�܂��B�@�V 6 ......[��]
�̂Ƃ�V�͍ő�ɂȂ�܂��B�@�V 6 ......[��]
V�̍ő�l�́A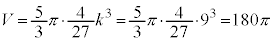 �@�X�Z�\ 180 ......[��]
�@�X�Z�\ 180 ......[��]
[2](1) 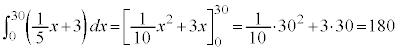 (��ϕ����Q��)�@�^�`�c 180 ......[��]
(��ϕ����Q��)�@�^�`�c 180 ......[��] 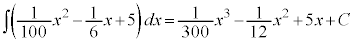 (�s��ϕ����Q��)�@�e�g�i 300�@�j�k 12�@�l 5 ......[��]
(�s��ϕ����Q��)�@�e�g�i 300�@�j�k 12�@�l 5 ......[��]
(2)(i) 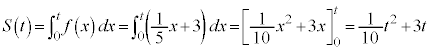
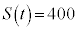 �ƂȂ����Ƃ��ɊJ�Ԃ���̂ŁA
�ƂȂ����Ƃ��ɊJ�Ԃ���̂ŁA�܂�A2���ɓ����Ă���50����ɊJ�Ԃ��܂��B�@�m 4 ......[��]
(ii) 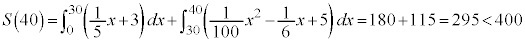
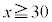 �ɂ�����
�ɂ�����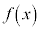 �͑�������̂ŁA
�͑�������̂ŁA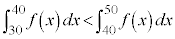 �@�n 0 ......[��]������A
�@�n 0 ......[��]������A����āA�\���C���V�m��40����ɂ͊J�Ԃ��Ă��炸�A50����ɂ͊��ɊJ�Ԃ��Ă��܂��B�܂�A40�������A����50������O�ɊJ�Ԃ��܂��B�@�q 4 ......[��]
���D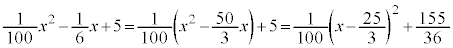 �ƂȂ�̂ŁA
�ƂȂ�̂ŁA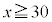 �ɂ�����
�ɂ�����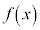 �͑����ł��B�܂��A
�͑����ł��B�܂��A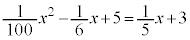 �Ƃ���ƁA
�Ƃ���ƁA ���A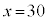 �ȊO�ɁA
�ȊO�ɁA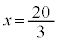 �ɂ����Ă��l����v���܂��B
�ɂ����Ă��l����v���܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 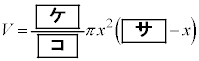 �@(
�@(