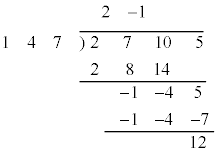�@���ʃe�X�g���wIIB '24�N��1��@
[1](1) 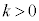 �C
�C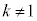 �Ƃ���B��
�Ƃ���B��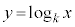 ��
��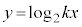 �̃O���t�ɂ��čl���悤�B
�̃O���t�ɂ��čl���悤�B (i) 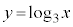 �̃O���t�͓_
�̃O���t�͓_ ��ʂ�B�܂��A
��ʂ�B�܂��A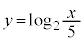 �̃O���t�͓_
�̃O���t�͓_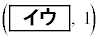 ��ʂ�B
��ʂ�B (ii) 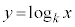 �̃O���t�́Ak�̒l�ɂ�炸��_
�̃O���t�́Ak�̒l�ɂ�炸��_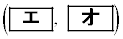 ��ʂ�B
��ʂ�B 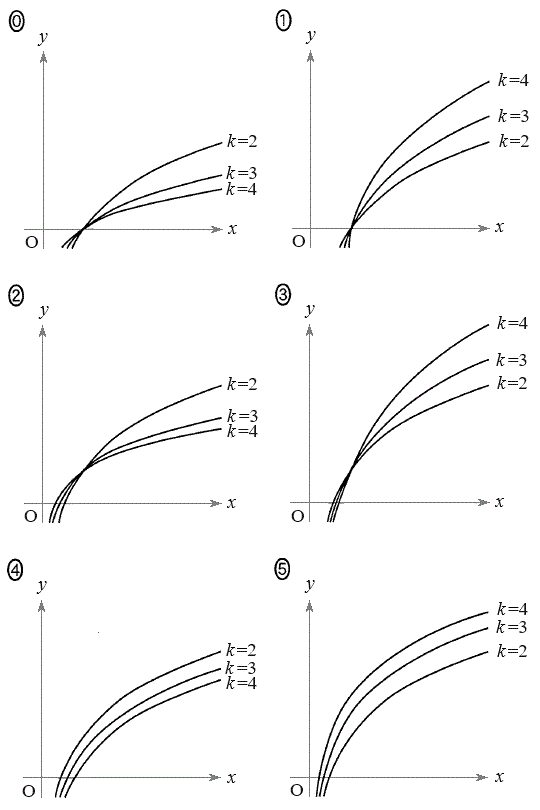 (iii)
(iii) 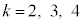 �̂Ƃ��A
�̂Ƃ��A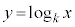 �̃O���t�̊T�`��
�̃O���t�̊T�`��
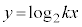 �̃O���t�̊T�`��
�̃O���t�̊T�`��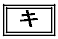
�ł���B
 �C
�C �ɂ��ẮA�ł��K���Ȃ��̂��A�E�}��
�ɂ��ẮA�ł��K���Ȃ��̂��A�E�}�� �`
�` �̂����������I�ׁB�������A�������̂��J��Ԃ��I��ł��悢�B
�̂����������I�ׁB�������A�������̂��J��Ԃ��I��ł��悢�B (2) 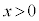 �C
�C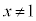 �C
�C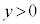 �Ƃ���B
�Ƃ���B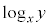 �ɂ��čl���悤�B
�ɂ��čl���悤�B
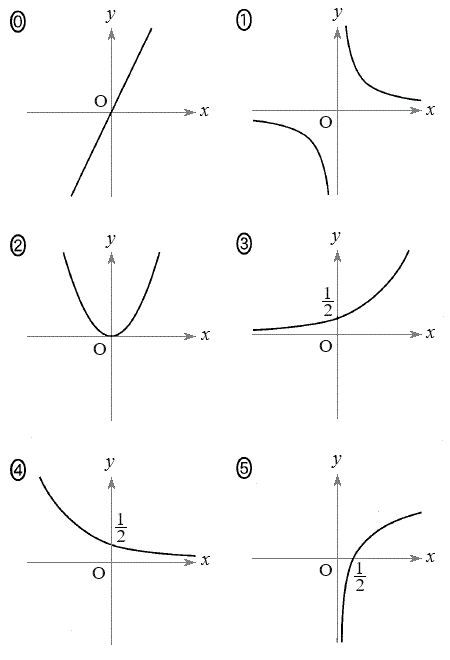 (i) ���W���ʂɂ����āA������
(i) ���W���ʂɂ����āA������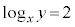 �̕\���}�`��}������ƁA
�̕\���}�`��}������ƁA ��
��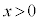 �C
�C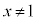 �C
�C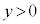 �̕����ƂȂ�B
�̕����ƂȂ�B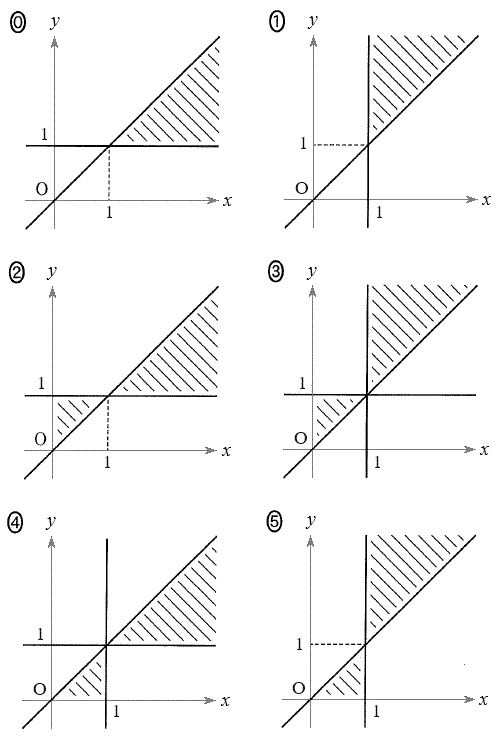 (ii) ���W���ʂɂ����āA�s����
(ii) ���W���ʂɂ����āA�s����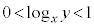 �̕\���̈��}������ƁA
�̕\���̈��}������ƁA �̎ΐ������ƂȂ�B�������A���E(���E��)�͊܂܂Ȃ��B
�̎ΐ������ƂȂ�B�������A���E(���E��)�͊܂܂Ȃ��B �ɂ��ẮA�ł��K���Ȃ��̂��A�E�}��
�ɂ��ẮA�ł��K���Ȃ��̂��A�E�}�� �`
�` �̂��������I�ׁB
�̂��������I�ׁB
[2]�@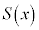 ��x��2�����Ƃ���Bx�̐���
��x��2�����Ƃ���Bx�̐���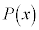 ��
��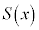 �Ŋ������Ƃ��̏���
�Ŋ������Ƃ��̏���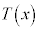 �C�]���
�C�]���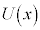 �Ƃ���B�������A
�Ƃ���B�������A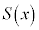 ��
��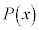 �̌W���͎����ł���Ƃ���B
�̌W���͎����ł���Ƃ���B
(1) 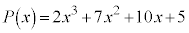 �C
�C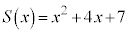 �̏ꍇ���l����B
�̏ꍇ���l����B ������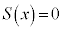 �̉���
�̉���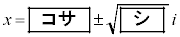 �ł���B
�ł���B
�܂��A �C
�C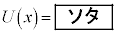 �ł���B
�ł���B
(2) ������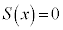 �͈قȂ��̉�α�Cβ�����Ƃ���B���̂Ƃ�
�͈قȂ��̉�α�Cβ�����Ƃ���B���̂Ƃ� 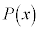 ��
��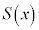 �Ŋ������]�肪�萔�ɂȂ�
�Ŋ������]�肪�萔�ɂȂ����ƂƓ��l�ȏ������l����B
(i) �]�肪�萔�ɂȂ�Ƃ����l���Ă݂悤�B
���肩��A�萔k��p����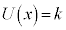 �Ƃ�����B���̂Ƃ��A
�Ƃ�����B���̂Ƃ��A �B���������āA�]�肪�萔�ɂȂ�Ƃ��A
�B���������āA�]�肪�萔�ɂȂ�Ƃ��A �����藧�B
�����藧�B
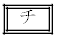 �ɂ��ẮA�ł��K���Ȃ��̂��A����
�ɂ��ẮA�ł��K���Ȃ��̂��A���� �`
�` �̂��������I�ׁB
�̂��������I�ׁB  �@
�@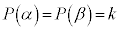 �����藧���Ƃ���A
�����藧���Ƃ���A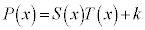 �ƂȂ邱�Ƃ��������B�܂��A
�ƂȂ邱�Ƃ��������B�܂��A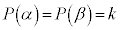 �����藧���Ƃ���A
�����藧���Ƃ���A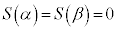 �ƂȂ邱�Ƃ��������B
�ƂȂ邱�Ƃ��������B �@
�@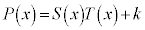 ����
����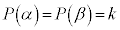 �����藧���Ƃ���A
�����藧���Ƃ���A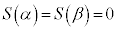 �ƂȂ邱�Ƃ��������B
�ƂȂ邱�Ƃ��������B �@
�@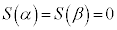 �����藧���Ƃ���A
�����藧���Ƃ���A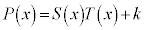 �ƂȂ邱�Ƃ��������B�܂��A
�ƂȂ邱�Ƃ��������B�܂��A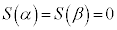 �����藧���Ƃ���A
�����藧���Ƃ���A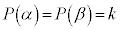 �ƂȂ邱�Ƃ��������B
�ƂȂ邱�Ƃ��������B �@
�@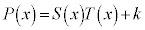 ����
����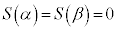 �����藧���Ƃ���A
�����藧���Ƃ���A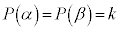 �ƂȂ邱�Ƃ��������B
�ƂȂ邱�Ƃ��������B �̉Q
�̉Q(ii) �t�� �����藧�Ƃ��A�]�肪�萔�ɂȂ邩���ׂ悤�B
�����藧�Ƃ��A�]�肪�萔�ɂȂ邩���ׂ悤�B 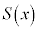 ��2�����ł��邩��Am�Cn��萔�Ƃ���
��2�����ł��邩��Am�Cn��萔�Ƃ���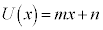 �Ƃ�����B
�Ƃ�����B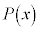 ��
��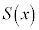 �C
�C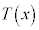 �Cm�Cn��p���ĕ\���ƁA
�Cm�Cn��p���ĕ\���ƁA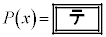 �ƂȂ�B���̓�����x��α�Cβ�����ꂼ���������
�ƂȂ�B���̓�����x��α�Cβ�����ꂼ���������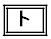 �ƂȂ�̂ŁA
�ƂȂ�̂ŁA ��
��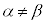 ���
���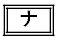 �ƂȂ�B�ȏォ��]�肪�萔�ɂȂ邱�Ƃ��킩��B
�ƂȂ�B�ȏォ��]�肪�萔�ɂȂ邱�Ƃ��킩��B
 �̉Q
�̉Q �̉Q
�̉Q �@
�@
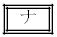 �̉Q
�̉Q �@
�@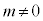 �@�@
�@�@ �@
�@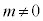 �@���@
�@���@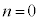
 �@
�@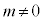 �@���@
�@���@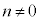 �@�@
�@�@ �@
�@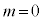
 �@
�@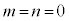 �@�@
�@�@ �@
�@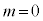 �@���@
�@���@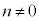
 �@
�@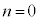 �@�@
�@�@ �@
�@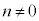
(i)�C(ii)�̍l�@����A������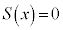 ���قȂ��̉�α�Cβ�����Ƃ��A
���قȂ��̉�α�Cβ�����Ƃ��A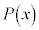 ��
��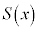 �Ŋ������]�肪�萔�ɂȂ邱�Ƃ�
�Ŋ������]�肪�萔�ɂȂ邱�Ƃ� �ł��邱�ƂƂ͓��l�ł���B
�ł��邱�ƂƂ͓��l�ł���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@��Փx�Ƃ��ẮA���̒��x�����ʃe�X�g�ɂӂ��킵���Ǝv���܂����A���t�V�т̂悤��[�`]�C[�c]�̐ݖ�͍l�����̂ł��B
[1](1)(i) 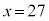 �̂Ƃ�
�̂Ƃ�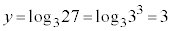 ���(�ΐ������Q��)�A
���(�ΐ������Q��)�A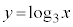 �̃O���t�͓_
�̃O���t�͓_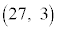 ��ʂ�B�@�A 3 ......[��]
��ʂ�B�@�A 3 ......[��] 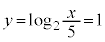 �Ƃ���ƁA
�Ƃ���ƁA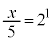 �@��
�@�� 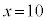 �C
�C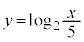 �̃O���t�͓_
�̃O���t�͓_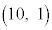 ��ʂ�B�@�C�E 10 ......[��]
��ʂ�B�@�C�E 10 ......[��](ii) 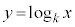 �̃O���t�́Ak�̒l�ɂ�炸��_
�̃O���t�́Ak�̒l�ɂ�炸��_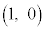 ��ʂ�܂��B�@�G 1�@�I 0 ......[��]
��ʂ�܂��B�@�G 1�@�I 0 ......[��] (iii) 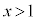 �ɂ����āA
�ɂ����āA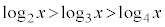 �ł��B(ii)���l�����āA
�ł��B(ii)���l�����āA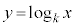 �̃O���t�̊T�`��
�̃O���t�̊T�`�� �ł��B�@�J 0 ......[��]
�ł��B�@�J 0 ......[��] 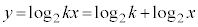 �C
�C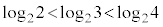 ���A
���A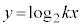 �̃O���t�̊T�`��
�̃O���t�̊T�`�� �ł��B�@�L 5 ......[��]
�ł��B�@�L 5 ......[��]
(2)(i) 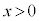 �C
�C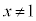 �C
�C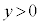 �̂Ƃ��A
�̂Ƃ��A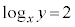 ��
�� 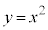 �@�N 2 ......[��]
�@�N 2 ......[��] �����\���̈��� �ł��B�@�P 2 ......[��]
�ł��B�@�P 2 ......[��]
[2]�@x�̐���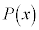 ��
��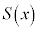 �Ŋ������Ƃ��̏���
�Ŋ������Ƃ��̏���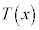 �C�]���
�C�]���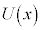 �Ƃ����(�������̏��Z���Q��)�A
�Ƃ����(�������̏��Z���Q��)�A
(1) 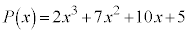 �C
�C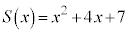
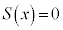 �Ƃ���ƁA
�Ƃ���ƁA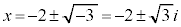 �@�R�T �|2�@�V 3 ......[��]����Z�����s����ƁA
�@�R�T �|2�@�V 3 ......[��]����Z�����s����ƁA����āA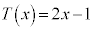 �C
�C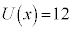 �@�X 2�@�Z 1�@�\�^ 12 ......[��]
�@�X 2�@�Z 1�@�\�^ 12 ......[��]
(2) 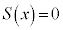 ����̉�α�Cβ������ ��
����̉�α�Cβ������ �� 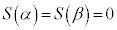 �@����@
�@����@ (i) �]�肪�萔�ɂȂ�Ƃ��A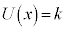 (k�F�萔)�C�܂�A
(k�F�萔)�C�܂�A 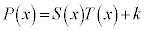 �@����A
�@����A[�`]�̑I�����͂ǂ�����ł͂Ȃ������悤�Ɍ����܂����A ��
�� �́A�A�͓������킯�ł͂Ȃ��̂ŕs�K�A
�́A�A�͓������킯�ł͂Ȃ��̂ŕs�K�A �́A�@�͓������킯�łȂ��̂ŕs�K�A
�́A�@�͓������킯�łȂ��̂ŕs�K�A �́A�u�A���@�����藧���Ƃ���v�ƌ����Ă���̂ŁA�����I�т܂��B�@�` 3 ......[��]�]�肪�萔�ɂȂ�Ƃ�������̂́A
�́A�u�A���@�����藧���Ƃ���v�ƌ����Ă���̂ŁA�����I�т܂��B�@�` 3 ......[��]�]�肪�萔�ɂȂ�Ƃ�������̂́A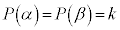 �����ł�(�����藝���Q��)�B�@�c 1 ......[��]
�����ł�(�����藝���Q��)�B�@�c 1 ......[��] (ii) 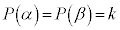 �@����B�C
�@����B�C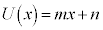 (m�Cn�F�萔)�Ƃ����ƁA
(m�Cn�F�萔)�Ƃ����ƁA 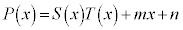 �@����C�@�e 1 ......[��]
�@����C�@�e 1 ......[��]�C��x��α��������ƁA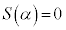 ���A
���A �C��x��β��������ƁA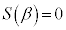 ���A
���A ����āA�g 1 ......[��]�B���A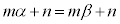
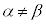 ���A
���A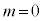 �@�i 3 ......[��]�ȏ���A�]��͒萔�ł��B
�@�i 3 ......[��]�ȏ���A�]��͒萔�ł��B
(3) 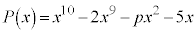 �C
�C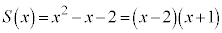
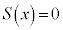 ��2���́A
��2���́A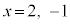 (2)���A
(2)���A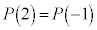 �̒l���萔�ƂȂ�]��ł��B
�̒l���萔�ƂȂ�]��ł��B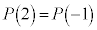 ���A
���A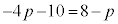 �@��
�@�� 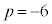 �@�j�k �|6 ......[��]�]��́A
�@�j�k �|6 ......[��]�]��́A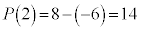 �@�l�m 14 ......[��]
�@�l�m 14 ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B