�@���ʃe�X�g���wIIB '24�N��4��@
(1) ����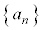 ��
�� 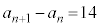 (
(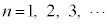 )
)�����Ƃ���B
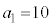 �̂Ƃ��A
�̂Ƃ��A �C
�C �ł���B
�ł���B
����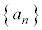 �̈�ʍ��́A����
�̈�ʍ��́A����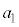 ��p����
��p���� �ƕ\�����Ƃ��ł���B
(2) ����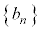 ��
�� 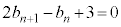 (
(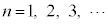 )
)�����Ƃ���B
����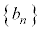 �̈�ʍ��́A����
�̈�ʍ��́A����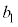 ��p����
��p���� �ƕ\�����Ƃ��ł���B
(3) ���Y����́A
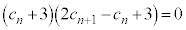 (
(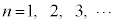 )�@����@
)�@����@��������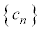 �ɂ��Ē��ׂ邱�Ƃɂ����B
�ɂ��Ē��ׂ邱�Ƃɂ����B (i)
�E����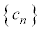 ���@�����A
���@�����A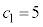 �̂Ƃ��A
�̂Ƃ��A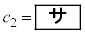 �ł���B
�ł���B �E����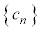 ���@�����A
���@�����A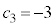 �̂Ƃ��A
�̂Ƃ��A �C
�C �ł���B
�ł���B (ii) ���Y����́A����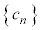 ���@�����A
���@�����A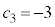 �ƂȂ�ꍇ�ɂ��čl���Ă���B
�ƂȂ�ꍇ�ɂ��čl���Ă���B 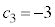 �̂Ƃ��A
�̂Ƃ��A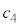 ���ǂ̂悤�Ȓl�ł�
���ǂ̂悤�Ȓl�ł������藧�B
(iii) ���Y�����(i)��(ii)����A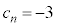 �ƂȂ邱�Ƃ����邩�ǂ����ɒ��ڂ��A��������A�����藧�̂ł͂Ȃ����ƍl�����B
�ƂȂ邱�Ƃ����邩�ǂ����ɒ��ڂ��A��������A�����藧�̂ł͂Ȃ����ƍl�����B
�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|
����A�@����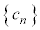 ���@�����A
���@�����A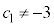 �ł���Ƃ���B���̂Ƃ��A���ׂĂ̎��R��n�ɂ���
�ł���Ƃ���B���̂Ƃ��A���ׂĂ̎��R��n�ɂ���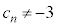 �ł���B
�ł���B �|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|����A���^�ł��邱�Ƃ��ؖ�����ɂ́A����A�̉����������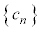 �ɂ��āA
�ɂ��āA �������悢�B
�������悢�B
���ہA���̂悤�ɂ�������A���^�ł��邱�Ƃ��ؖ��ł���B
 �ɂ��ẮA�ł��K���Ȃ��̂��A����
�ɂ��ẮA�ł��K���Ȃ��̂��A���� �`
�` �̂��������I�ׁB
�̂��������I�ׁB  �@
�@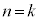 �̂Ƃ�
�̂Ƃ�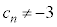 �����藧�Ɖ��肷��ƁA
�����藧�Ɖ��肷��ƁA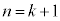 �̂Ƃ���
�̂Ƃ���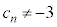 �����藧����
�����藧���� �@
�@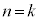 �̂Ƃ�
�̂Ƃ�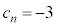 �����藧�Ɖ��肷��ƁA
�����藧�Ɖ��肷��ƁA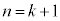 �̂Ƃ���
�̂Ƃ���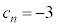 �����藧����
�����藧����(iv) ����(�T)�C(�U)�C(�V)�́A����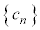 �Ɋւ��閽��ł���B
�Ɋւ��閽��ł���B (�T)�@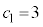 ����
����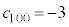 �ł���A���@��������
�ł���A���@��������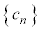 ������B
������B (�U)�@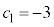 ����
����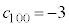 �ł���A���@��������
�ł���A���@��������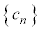 ������B
������B (�V)�@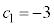 ����
����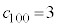 �ł���A���@��������
�ł���A���@��������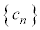 ������B
������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�]���̐���̖��Ɣ�ׂĂ��Ȃ�y�����������܂����A�ǂ��X���ł��B
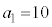 �̂Ƃ��A�A��
�̂Ƃ��A�A��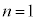 �Ƃ��āA
�Ƃ��āA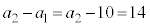 �@��
�@�� 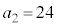 �@�A�C 24 ......[��]�A��
�@�A�C 24 ......[��]�A��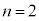 �Ƃ��āA
�Ƃ��āA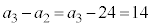 �@���@
�@���@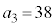 �@�E�G 38 ......[��]�K�������̌�����p���āA
�@�E�G 38 ......[��]�K�������̌�����p���āA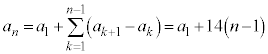 �@�I�J 14 ......[��]
�@�I�J 14 ......[��]
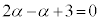 �@����C�@�Ƃ���ƁA
�@����C�@�Ƃ���ƁA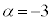
�B�|�C���A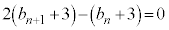
�� 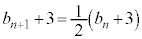 ����
����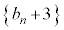 �́A����
�́A����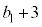 �C����
�C����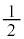 �����䐔���B
�����䐔���B
�� 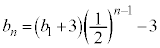 �@�L 3�@�N 1�@�P 2�@�R 3 ......[��]
�@�L 3�@�N 1�@�P 2�@�R 3 ......[��]
(3) 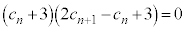 (
(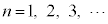 )�@����@
)�@����@
(i)�E�@��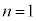 �Ƃ���ƁA
�Ƃ���ƁA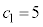 �̂Ƃ��A
�̂Ƃ��A �E�@��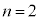 �Ƃ���ƁA
�Ƃ���ƁA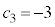 �̂Ƃ��A
�̂Ƃ��A 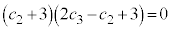
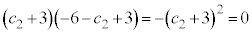 �@��
�@�� 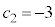 �@�V�X �|3 ......[��]
�@�V�X �|3 ......[��]�@��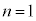 �Ƃ���ƁA
�Ƃ���ƁA 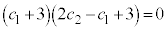
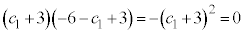 �@��
�@�� 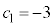 �@�Z�\ �|3 ......[��]
�@�Z�\ �|3 ......[��](ii) �E�@��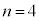 �Ƃ���ƁA
�Ƃ���ƁA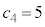 �̂Ƃ��A
�̂Ƃ��A �E�@��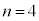 �Ƃ���ƁA
�Ƃ���ƁA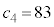 �̂Ƃ��A
�̂Ƃ��A 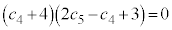
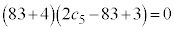 �@��
�@�� 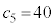 �@�`�c 40 ......[��]
�@�`�c 40 ......[��]�E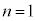 �̂Ƃ��A
�̂Ƃ��A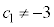 �Ȃ̂ŁA����A�͐��藧���܂��B
�Ȃ̂ŁA����A�͐��藧���܂��B �E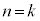 �̂Ƃ�����A�����藧�Ɖ��肷��ƁA
�̂Ƃ�����A�����藧�Ɖ��肷��ƁA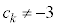
�@��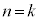 �Ƃ���ƁA
�Ƃ���ƁA
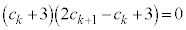
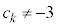 �Ȃ̂ŁA
�Ȃ̂ŁA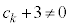 ���A
���A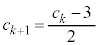 �ł����A����
�ł����A����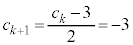 �Ƃ���ƁA
�Ƃ���ƁA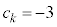 �ɂȂ��Ă��܂��̂ŁA
�ɂȂ��Ă��܂��̂ŁA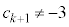 �ł���A
�ł���A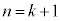 �̂Ƃ�������A�����藧���܂��B
�̂Ƃ�������A�����藧���܂��B ����āA���w�I�A�[�@�ɂ��A����A�����藧���܂��B�@�e 3 ......[��]
(iv) ����(�T)�F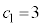 �Ȃ̂ŁA����A�ɂ��A���ׂĂ̎��R��n�ɂ���
�Ȃ̂ŁA����A�ɂ��A���ׂĂ̎��R��n�ɂ���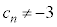 �Ȃ̂�
�Ȃ̂�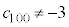 �ł����āA����(�T)�͋U�ł��B
�ł����āA����(�T)�͋U�ł��B ����(�U)�F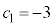 �ł���A
�ł���A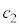 ���ǂ�Ȓl�ł����Ă��@���������܂��B
���ǂ�Ȓl�ł����Ă��@���������܂��B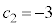 �ł���A
�ł���A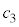 ���ǂ�Ȓl�ł����Ă��@���������܂��B������J��Ԃ��A
���ǂ�Ȓl�ł����Ă��@���������܂��B������J��Ԃ��A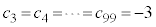 �ł���A
�ł���A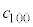 ���ǂ�Ȓl�ł����Ă��@���������܂��B
���ǂ�Ȓl�ł����Ă��@���������܂��B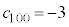 �ł����Ă��@���������܂��B����āA����(�U)�͐^�ł��B
�ł����Ă��@���������܂��B����āA����(�U)�͐^�ł��B ����(�V)�F����(�U)�Ɠ��l�A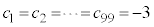 �ł���A
�ł���A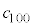 ���ǂ�Ȓl�ł����Ă��@���������܂��B
���ǂ�Ȓl�ł����Ă��@���������܂��B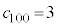 �ł����Ă��@���������܂��B����āA����(�V)�͐^�ł��B
�ł����Ă��@���������܂��B����āA����(�V)�͐^�ł��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 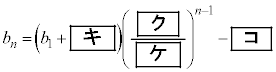
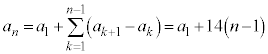 �@�I�J 14 ......[��]
�@�I�J 14 ......[��]