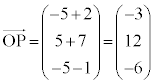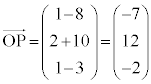�@���ʃe�X�g���wIIB '24�N��5��@
�_O�����_�Ƃ�����W��Ԃ�4�_A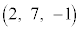 �CB
�CB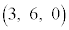 �CC
�CC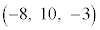 �CD
�CD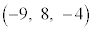 ������BA�CB��ʂ钼����
������BA�CB��ʂ钼����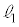 �Ƃ��AC�CD��ʂ钼����
�Ƃ��AC�CD��ʂ钼����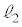 �Ƃ���B
�Ƃ���B
(1) 
�ł���A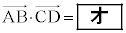 �ł���B
�ł���B
(2) �Ԏq����Ƒ��Y����́A�_P��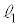 ����Ƃ��A
����Ƃ��A ���ŏ��ƂȂ�P�̈ʒu�ɂ��čl���Ă���B
���ŏ��ƂȂ�P�̈ʒu�ɂ��čl���Ă���B P��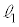 ��ɂ���̂ŁA
��ɂ���̂ŁA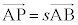 ��������s������A
��������s������A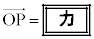 �����藧�B
�����藧�B
 ���ŏ��ƂȂ�s�̈ʒu�����߂��P�̈ʒu�����܂�B���̂��Ƃɂ��āA�Ԏq����Ƒ��Y���b�����Ă���B
���ŏ��ƂȂ�s�̈ʒu�����߂��P�̈ʒu�����܂�B���̂��Ƃɂ��āA�Ԏq����Ƒ��Y���b�����Ă���B
�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�| �Ԏq�F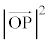 ���ŏ��ƂȂ�s�̒l�����߂�悢�ˁB
���ŏ��ƂȂ�s�̒l�����߂�悢�ˁB ���Y�F ���ŏ��ƂȂ�Ƃ��̒���OP��
���ŏ��ƂȂ�Ƃ��̒���OP��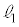 �̊W�ɒ��ڂ��Ă��悳��������B
�̊W�ɒ��ڂ��Ă��悳��������B �|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|
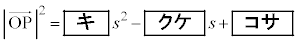 �ł���B
�ł���B
�܂��A ���ŏ��ƂȂ�Ƃ��A����OP��
���ŏ��ƂȂ�Ƃ��A����OP��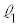 �̊W�ɒ��ڂ����
�̊W�ɒ��ڂ���� �����藧���Ƃ��킩��B
�����藧���Ƃ��킩��B
�Ԏq����̍l�����ł��A���Y����̍l�����ł��A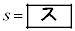 �̂Ƃ�
�̂Ƃ� ���ŏ��ƂȂ邱�Ƃ��킩��B
���ŏ��ƂȂ邱�Ƃ��킩��B
 �̉Q
�̉Q  �̉Q
�̉Q �@
�@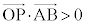 �@�@
�@�@ �@
�@
 �@
�@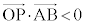 �@�@
�@�@ �@
�@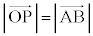
 �@
�@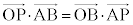 �@�@
�@�@ �@
�@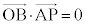
 �@
�@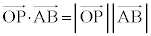
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�Ō�̃Z�\�^�`�c�e�g�i�j�k�l�m�������āA��N�̃x�N�g�����������Ɗ�{�I���ł��B�Ō���A���ẮA�p�o�W�����ł����B�Ȃ��A��ԃx�N�g�����Q�Ƃ��Ă��������B
(1) 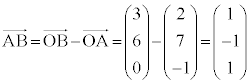 �@�A 1�@�C�E �|1�@�G 1 ......[��]�@����@
�@�A 1�@�C�E �|1�@�G 1 ......[��]�@����@ 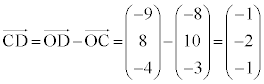 �@����A
�@����A
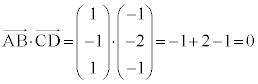 �@�I 0 ......[��]
�@�I 0 ......[��]�܂�A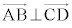 �C
�C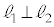 �ł��B
�ł��B
(2) 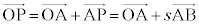 �@�J 2 ......[��]
�@�J 2 ......[��]
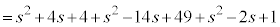
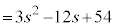 �@�L 3�@�N�P 12�@�R�T 54 ......[��]
�@�L 3�@�N�P 12�@�R�T 54 ......[��]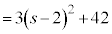
������A�Ԏq����̍l�����ŁA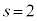 �̂Ƃ�
�̂Ƃ� �ŏ��ł��B
�ŏ��ł��B
 �ŏ��̂Ƃ��A
�ŏ��̂Ƃ��A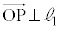 �Ȃ̂ŁA
�Ȃ̂ŁA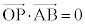 �ł��B�@�V 1 ......[��]���Y����̍l�����ŁA�@�C�B���A
�ł��B�@�V 1 ......[��]���Y����̍l�����ŁA�@�C�B���A 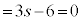 �@��
�@�� 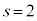 �@�X 2 ......[��]
�@�X 2 ......[��]
(3) �A��p���āA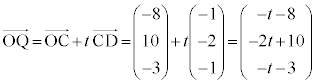 �@����C
�@����C
�B�C�C���A
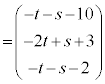 �@����D
�@����D�Ԏq����̍l�����ł́A
�̍ŏ��l�ׂ�̂ł����A�v�Z����ςł��B
�����ŁA���Y����̍l�����ł���Ă݂܂��B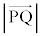 �ŏ��̂Ƃ��A
�ŏ��̂Ƃ��A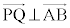 ����
����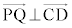 �ƂȂ�̂ŁA
�ƂȂ�̂ŁA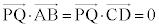 (�������Q��)�ł��B�@�C�D���A
(�������Q��)�ł��B�@�C�D���A �B�ɑ�����āA
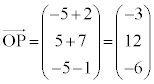 �@�Z�\ �|3�@�^�` 12�@�c�e �|6 ......[��]
�@�Z�\ �|3�@�^�` 12�@�c�e �|6 ......[��]�D�ɑ�����āA
�C�ɑ�����āA
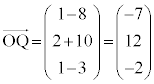 �@�g�i �|7�@�j�k 12�@�l�m �|2 ......[��]
�@�g�i �|7�@�j�k 12�@�l�m �|2 ......[��]�ʉ��D�{��ł́A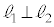 ���������Ĉȉ��̂悤�ɉ��邱�Ƃ��ł��܂��B
���������Ĉȉ��̂悤�ɉ��邱�Ƃ��ł��܂��B 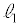 ��
��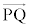 ���܂ޕ��ʂ�
���܂ޕ��ʂ�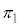 �C
�C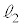 ��
��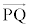 ���܂ޕ��ʂ�
���܂ޕ��ʂ�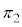 �Ƃ���ƁA
�Ƃ���ƁA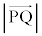 �ŏ��̂Ƃ��A
�ŏ��̂Ƃ��A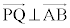 ����
����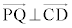 �Ȃ̂ŁA
�Ȃ̂ŁA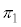 �̖@���x�N�g����
�̖@���x�N�g����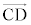 �C
�C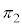 �̖@���x�N�g����
�̖@���x�N�g����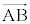 �ł��B����āA
�ł��B����āA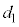 �C
�C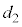 ��萔�Ƃ��āA���ʂ̕������́A
��萔�Ƃ��āA���ʂ̕������́A�Ƃ����܂��B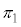 ��A
��A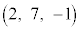 ��ʂ�̂�
��ʂ�̂� 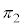 ��C
��C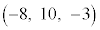 ��ʂ�̂ŁA
��ʂ�̂ŁA������A
P��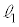 ��
��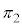 �̌�_�ŁA�B���A
�̌�_�ŁA�B���A 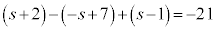 �@��
�@��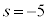
�B�ɑ�����āA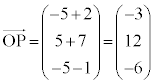 Q��
Q��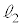 ��
��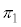 �̌�_�ŁA�C���A
�̌�_�ŁA�C���A 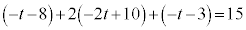 �@��
�@��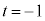
�C�ɑ�����āA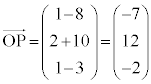
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 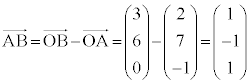 �@�A 1�@�C�E �|1�@�G 1 ......[��]�@����@
�@�A 1�@�C�E �|1�@�G 1 ......[��]�@����@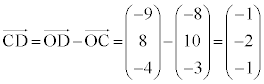 �@����A
�@����A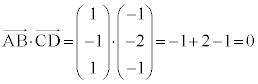 �@�I 0 ......[��]
�@�I 0 ......[��]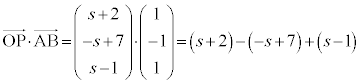
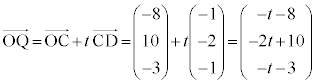 �@����C
�@����C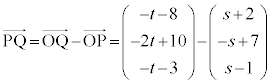
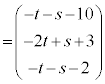 �@����D
�@����D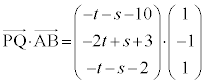
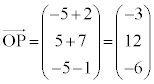 �@�Z�\ �|3�@�^�` 12�@�c�e �|6 ......[��]
�@�Z�\ �|3�@�^�` 12�@�c�e �|6 ......[��]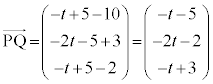
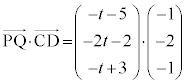
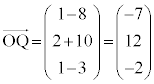 �@�g�i �|7�@�j�k 12�@�l�m �|2 ......[��]
�@�g�i �|7�@�j�k 12�@�l�m �|2 ......[��]