減衰振動関数 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
この項目については、物理への応用(その2)を参照してください。
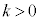 ,
,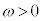 として、xの関数:
として、xの関数: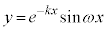 の挙動について調べます。
の挙動について調べます。
この関数は、xを時間とみると、減衰振動している物体の座標を表す関数です。
まず、グラフを調べてみます。
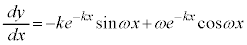
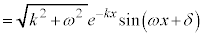
δは、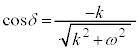 ,
,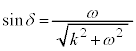 を満たす角で、
を満たす角で、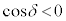 ,
,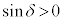 より第2象限の角 (
より第2象限の角 (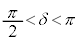 )。
)。
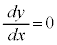 とすると、
とすると、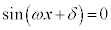
よって、nを整数として、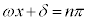
∴ 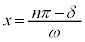
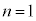 として、
として、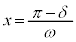 のとき、
のとき、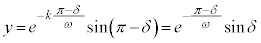
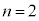 として、
として、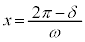 のとき、
のとき、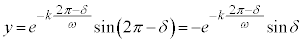
これより、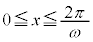 における増減表は以下のようになります。
における増減表は以下のようになります。
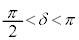 より、
より、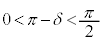 ,
,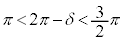 であることに注意してください。
であることに注意してください。
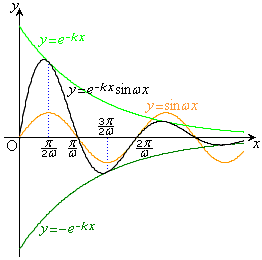 増減表より、グラフは右図(黒が
増減表より、グラフは右図(黒が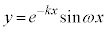 ,黄緑が
,黄緑が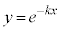 ,緑が
,緑が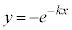 ,橙が
,橙が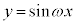 ,但し、見易いようにy方向の縮尺を曲線ごとに変えています)。
,但し、見易いようにy方向の縮尺を曲線ごとに変えています)。
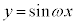 は、
は、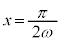 で極大、
で極大、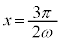 で極小になりますが、減衰振動関数:
で極小になりますが、減衰振動関数: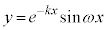 では、極大位置と極小位置が若干左にずれることに注意してください。
では、極大位置と極小位置が若干左にずれることに注意してください。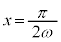 ,
,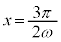 では、
では、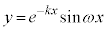 ,
,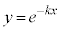 が共有点をもつだけで、減衰振動関数は、極大、極小にはなりません。
が共有点をもつだけで、減衰振動関数は、極大、極小にはなりません。
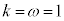 のときには、
のときには、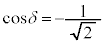 ,
,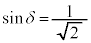 より、
より、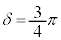 ,
,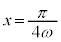 において極大、
において極大、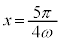 において極小。
において極小。
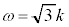 のときには、
のときには、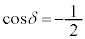 ,
,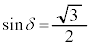 より、
より、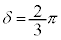 ,
,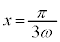 において極大、
において極大、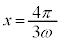 において極小。
において極小。
減衰振動関数: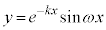 の
の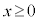 の部分とx軸で囲まれた部分の面積Sを求めるという問題が大学入試で頻出です。
の部分とx軸で囲まれた部分の面積Sを求めるという問題が大学入試で頻出です。
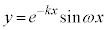 のグラフは、jを整数として、
のグラフは、jを整数として、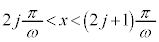 においては、
においては、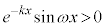 よりx軸の上側にあり、
よりx軸の上側にあり、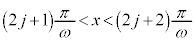 においては、
においては、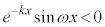 よりx軸の下側にきます。面積を計算するに当たり、定型的な考え方をするのであれば、x軸の上側にくる部分と、x軸の下側に来る部分とに分けて計算する必要があります。
よりx軸の下側にきます。面積を計算するに当たり、定型的な考え方をするのであれば、x軸の上側にくる部分と、x軸の下側に来る部分とに分けて計算する必要があります。
しかし、置換積分をすることにより、場合分けなしで計算する方法があります。
Sを式で表すと、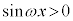 の範囲と
の範囲と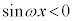 の範囲で積分区間を分ける必要があり、
の範囲で積分区間を分ける必要があり、
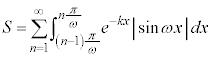
となります。
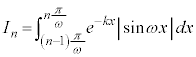
ここで、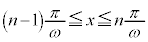 となっている積分区間を、
となっている積分区間を、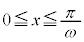 とするために、
とするために、
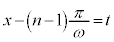
とおきます。この置き換えをしっかり覚えてください。
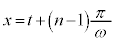
tで両辺を微分して、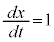
∴ 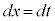
x: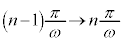 のとき、t:
のとき、t: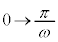
よって、
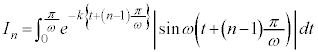
ここで、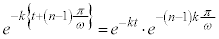 であり、
であり、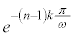 にはtが含まれず、tに関する積分の外に出すことができます。また、
にはtが含まれず、tに関する積分の外に出すことができます。また、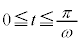 つまり、
つまり、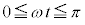 においては、
においては、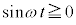 なので、
なので、
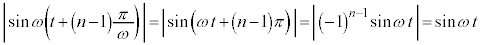
従って、
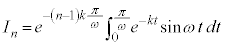
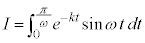 (部分積分法を参照)
(部分積分法を参照)
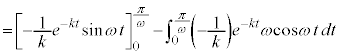
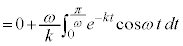
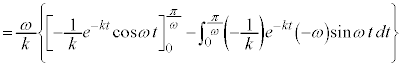
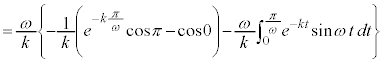
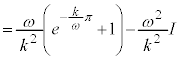
∴ 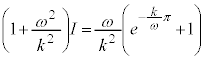
∴ 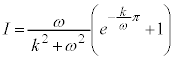
∴ 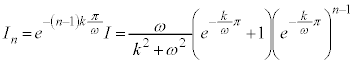
よって、求める面積Sは、
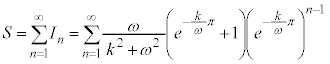
これは、初項: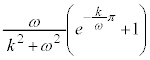 ,公比:
,公比: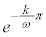 の無限等比級数であって、
の無限等比級数であって、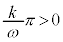 より、
より、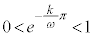 であり、無限等比級数は収束して和を持ちます。従って、
であり、無限等比級数は収束して和を持ちます。従って、
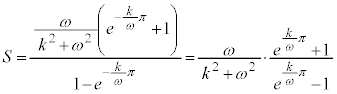 (最後に分母・分子に
(最後に分母・分子に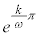 をかけました)
をかけました)
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 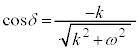 ,
,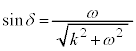 を満たす角で、
を満たす角で、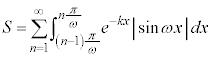
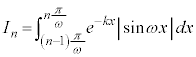
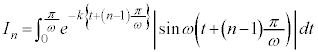
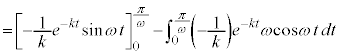
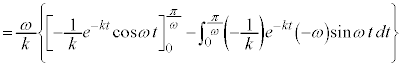
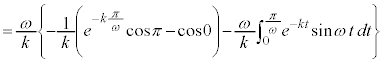
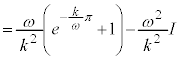
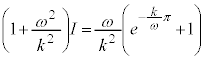
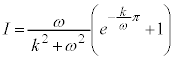
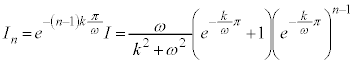
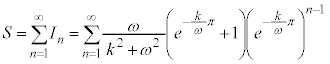
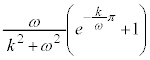 ,公比:
,公比: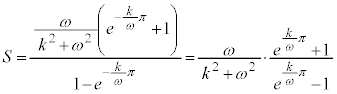 (最後に分母・分子に
(最後に分母・分子に