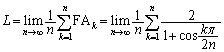熊本大理系数学'08年[4]
放物線C: および点F
および点F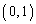 について考える。以下の問いに答えよ。ただし、Oは原点を表す。
について考える。以下の問いに答えよ。ただし、Oは原点を表す。
(1) 放物線C上の点A (
( とする)に対して
とする)に対して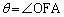 ,
,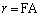 とおく。rをθ を用いて表せ。
とおく。rをθ を用いて表せ。 を満たすようにとる。極限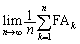 を求めよ。
を求めよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
 解答 放物線
解答 放物線 の焦点は
の焦点は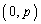 ,準線は
,準線は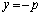 です。
です。
(2)は、 は気がつけても、
は気がつけても、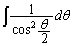 だと気がつきにくいかも知れません。試験会場では、
だと気がつきにくいかも知れません。試験会場では、 を微分してみるとよいと思います。
を微分してみるとよいと思います。
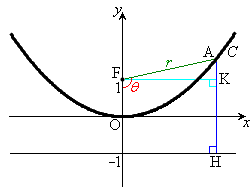
A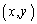 から準線に垂線AHを下ろすと、H
から準線に垂線AHを下ろすと、H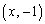 です。FからAHに垂線FKを下ろすと、
です。FからAHに垂線FKを下ろすと、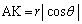 ですが、
ですが、
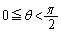 について、
について、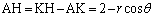
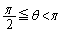 について、
について、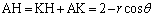
放物線上の点Aから焦点Fまでの距離と、点Aから準線までの距離AHは等しいので、
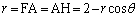
∴  ......[答]追記.ここで得られた関係式は、放物線の、焦点Fを極とする極座標表示になっています。曲線上の点Aと定点Fまでの距離AF,Aから定直線に下ろした垂線をAHとして、
......[答]追記.ここで得られた関係式は、放物線の、焦点Fを極とする極座標表示になっています。曲線上の点Aと定点Fまでの距離AF,Aから定直線に下ろした垂線をAHとして、 が定数になるとき、eを離心率と言います。この問題では、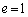 であって、曲線は放物線になります。
であって、曲線は放物線になります。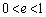 では、曲線は楕円になり、
では、曲線は楕円になり、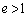 では双曲線になります。定点Fを焦点、定直線を準線と言います。なお、極座標を参照してください。
では双曲線になります。定点Fを焦点、定直線を準線と言います。なお、極座標を参照してください。
(2) (1)で導いた関係式で、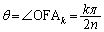 のとき、
のとき、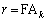 だとして、
だとして、 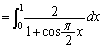 (
(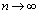 のとき、
のとき、 ,
, ,
,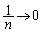 ,
,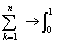 ,
,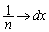 と見て定積分に直します。区分求積法を参照)
と見て定積分に直します。区分求積法を参照)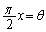 とおくと、
とおくと、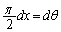 ,x:
,x: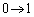 のとき、θ :
のとき、θ :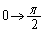 (置換積分を参照)
(置換積分を参照)
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。