�O�d�勳�琔�w'08�N[1]
���W���ʂɂ����āA�_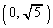 ��ʂ�~C�F
��ʂ�~C�F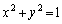 �Ƒ�1�ی��̓_�Őڂ��钼����
�Ƒ�1�ی��̓_�Őڂ��钼���� �Ƃ���B�܂��A����
�Ƃ���B�܂��A���� �ƒ������~C�Ƒ�4�ی��̓_�Őڂ��钼����
�ƒ������~C�Ƒ�4�ی��̓_�Őڂ��钼����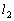 �Ƃ���B���̂Ƃ��ȉ��̖₢�ɓ�����B
�Ƃ���B���̂Ƃ��ȉ��̖₢�ɓ�����B
(1) ����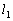 �̕����������߂�B
�̕����������߂�B (2) ����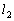 �̕����������߂�B
�̕����������߂�B (3) ���_��O�Ƃ��A2����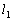 �C
�C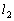 �̌�_��P�Ƃ���B2�_O�CP��ʂ钼����ɒ��S�����~
�̌�_��P�Ƃ���B2�_O�CP��ʂ钼����ɒ��S�����~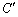 ��O��ʂ肳���
��O��ʂ肳���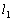 �Ɛڂ��Ă���Ƃ��A
�Ɛڂ��Ă���Ƃ��A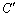 �̕����������߂�B
�̕����������߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�Z���^�[�����̗��K�p�ɁA�Ƃ���1��ł��B(3)�́}����₱�����̂ŁA�{�̏ꍇ�Ɓ|�̏ꍇ�Ƃŕ����ĉ�������ǂ������m��܂���B
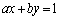 �@����@
�@����@�������A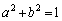 �@����A
�@����A
�@�͓_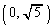 ��ʂ邩��A
��ʂ邩��A �� 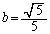 �A���A
�A���A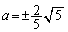
�~C�Ƈ@�͑�1�ی��Őڂ���̂ŁA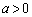 ���A
���A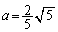
����āA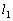 �F
�F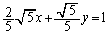
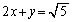 ......[��]�@����B
......[��]�@����B
(2) �~C�Ƒ�4�ی��̓_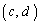 �Őڂ���ڐ��F
�Őڂ���ڐ��F �� 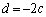 �C���A
�C���A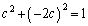
�� 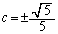
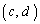 �͑�4�ی��̓_�Ȃ̂ŁA
�͑�4�ی��̓_�Ȃ̂ŁA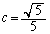 �C
�C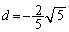
����āA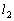 �F
�F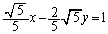
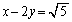 ......[��]�@����D
......[��]�@����D
(3) �B�C�D��A�����ĉ����ƁA
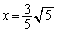 �C
�C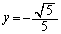
����āA �C
�C �̌�_��P
�̌�_��P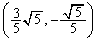
2�_O�CP��ʂ钼���́A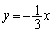 �@����E
�@����E
�E��̓_��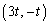 �ƕ\����̂ŁA���a��r�Ƃ��āA�~
�ƕ\����̂ŁA���a��r�Ƃ��āA�~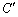 �����_O��ʂ邱�Ƃ���A
�����_O��ʂ邱�Ƃ���A �� 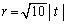 �@����F
�@����F
�܂��A�~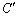 ��
��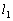 �ɐڂ��邱�Ƃ���A
�ɐڂ��邱�Ƃ���A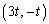 �ƇB�Ƃ̋�����r�ł�(�~�ƒ����̈ʒu�W���Q��)�B
�ƇB�Ƃ̋�����r�ł�(�~�ƒ����̈ʒu�W���Q��)�B �F�C�G���A
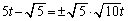
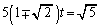
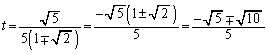 �@(��������)
�@(��������)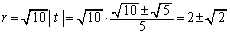 �@(��������)
�@(��������)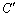 �F
�F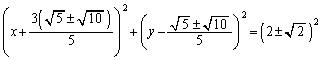 �@(��������) ......[��]
�@(��������) ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B  �@(��������)
�@(��������)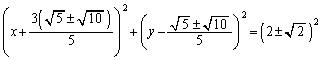 �@(��������) ......[��]
�@(��������) ......[��]