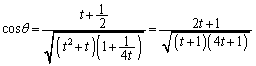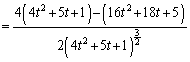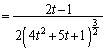���H�吔�w'08�N[2]
�Ȑ�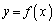 (
(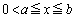 )��̓_P
)��̓_P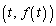 (
(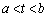 )�ɂ�����ڐ���l�Ƃ��Al��̓_�ł���x���W��
)�ɂ�����ڐ���l�Ƃ��Al��̓_�ł���x���W��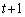 �ƂȂ�_��Q�Ƃ����B���_��O�Ƃ��Ď��̖₢�ɓ�����B
�ƂȂ�_��Q�Ƃ����B���_��O�Ƃ��Ď��̖₢�ɓ�����B
(1) 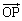 ��
��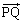 �̂Ȃ��p��θ �Ƃ���Ƃ��A
�̂Ȃ��p��θ �Ƃ���Ƃ��A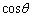 ��t��p���ĕ\���B
��t��p���ĕ\���B (2) 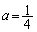 �C
�C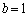 �C
�C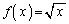 �̂Ƃ��Aθ ���ő�ƂȂ�t�����߂�B
�̂Ƃ��Aθ ���ő�ƂȂ�t�����߂�B (3) 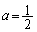 �C
�C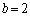 �Ƃ���B���ׂĂ�t (
�Ƃ���B���ׂĂ�t (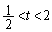 )�ɂ���
)�ɂ���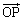 ��
��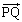 ���������A
���������A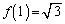 �ƂȂ�
�ƂȂ�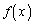 �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(3)�������������̖��ł����A���̒��x�Ȃ�u�����������v�ƌ�����قǂ̂��̂ł͂Ȃ��A�[���ɍ��Z�̌��s�w�K�w���v�͈͓̔��ł��B
(1) 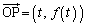
l�F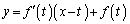
l�̎��ɂ�����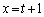 �Ƃ��āA
�Ƃ��āA �� 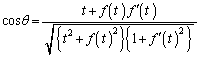 ......[��]θ �́A
......[��]θ �́A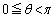 �Ƃ��čl���邱�Ƃɂ��܂��B
�Ƃ��čl���邱�Ƃɂ��܂��B
(2) 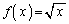 �̂Ƃ��A
�̂Ƃ��A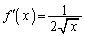
������(1)�̌��ʂɑ�����āA
�����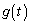 �Ƃ����ƁA
�Ƃ����ƁA 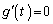 �Ƃ���ƁA
�Ƃ���ƁA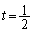 �����\���A
�����\���A �ɂ����āA
�ɂ����āA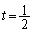 �̂Ƃ��ɁA
�̂Ƃ��ɁA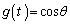 �͍ŏ�(���̑������Q��)�ŁA
�͍ŏ�(���̑������Q��)�ŁA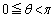 �Ƃ���ƁA���̂Ƃ���θ�ő�ƂȂ�܂�(θ �����傷��Ƃ��A
�Ƃ���ƁA���̂Ƃ���θ�ő�ƂȂ�܂�(θ �����傷��Ƃ��A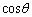 ���������邱�Ƃɒ���)�Bθ���ő�ƂȂ�t�́A
���������邱�Ƃɒ���)�Bθ���ő�ƂȂ�t�́A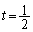 ......[��]
......[��]
(3) 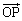 ��
��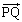 ���������邱�Ƃ���A
���������邱�Ƃ���A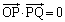 �@(�������Q��)
�@(�������Q��) �@���A
���ӂ�t�Őϕ�����ƁA
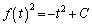 �@(C�F�ϕ��萔)
�@(C�F�ϕ��萔)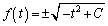
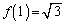 ���}�́{�̕����Ƃ�A
���}�́{�̕����Ƃ�A�� 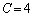
t��x�ɏ��������āA
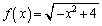 ......[��]
......[��]
�NjL�D���̖��Ɠ��l�̔��z��������ɁA'96�N�c�嗝�H[B1]�F
���W���ʏ���^������P�������āA����t�ɂ�������W��t�̔����\�Ȋ�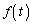 �C
�C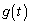 �ɂ����P
�ɂ����P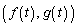 �ŗ^�����Ă���B�������W���ʏ���^����������ЂƂ̓_Q�������āA����t�ɂ�������W��Q
�ŗ^�����Ă���B�������W���ʏ���^����������ЂƂ̓_Q�������āA����t�ɂ�������W��Q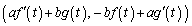 �ŗ^�����Ă���B������a�Cb�͒萔��
�ŗ^�����Ă���B������a�Cb�͒萔��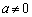 �ł���B����ɁA�x�N�g��
�ł���B����ɁA�x�N�g��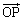 ��
��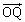 �͂˂ɒ������Ă�����̂Ƃ���B�������AO�͌��_
�͂˂ɒ������Ă�����̂Ƃ���B�������AO�͌��_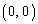 ��\���B���̂Ƃ����̖₢�ɓ�����B
��\���B���̂Ƃ����̖₢�ɓ�����B (1) �x�N�g��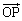 �̑傫��
�̑傫��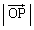 �͈��ł��邱�Ƃ������B
�͈��ł��邱�Ƃ������B (�ȉ��ȗ�)
������܂��B
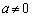 ���A
���A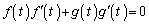 �ƂȂ�܂����A
�ƂȂ�܂����A
���H��̖��Ɠ��l�ɁA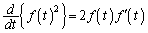 �C
�C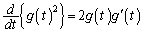 ���(�������̔����@���Q��)�A
���(�������̔����@���Q��)�A
t�Őϕ����āA
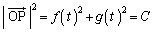 �@(C�F���)
�@(C�F���)
���̂悤�Ȗ����A�����������̖��Ƃ������܂����A���s�͈͓��ŏ[���ɉ\�ł��B
y���Ƃ̌�_��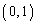 �ł���Ȑ�
�ł���Ȑ�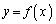 ��̓_
��̓_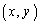 �ɂ�����ڐ��̌X����
�ɂ�����ڐ��̌X����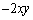 �̂Ƃ��A
�̂Ƃ��A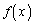 �͂ǂ�Ȋ����B�˂�
�͂ǂ�Ȋ����B�˂�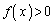 �Ƃ���B
�Ƃ���B
���@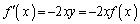
���ӂ�x�Őϕ�����ƁA
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 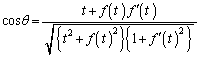 ......[��]
......[��]