���R�嗝�n���w'08�N[3]
a��0�ȏ�̎����An�𐳂̐����Ƃ���Ƃ��A���̖₢�ɓ�����B
(1) 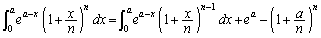
�����藧���Ƃ������B
(2) 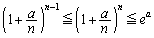 �����藧���Ƃ������B
�����藧���Ƃ������B (3) 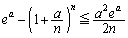 �����藧���Ƃ������B
�����藧���Ƃ������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�U�����Ȃ���Γ��ł����A�e�ȗU�������Ă���̂ŁA�U���ʂ�ɂ��Α債�����Ƃ͂���܂���B
(2)�C(3)���A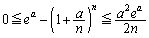 �C
�C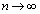 �̂Ƃ��A
�̂Ƃ��A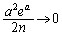 �Ȃ̂ŁA
�Ȃ̂ŁA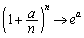 (
(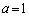 �̏ꍇ�ɂ��ẮA�Ɍ��̌������Q��)�ɂȂ�ƌ��������̂��낤�Ǝv���܂��B
�̏ꍇ�ɂ��ẮA�Ɍ��̌������Q��)�ɂȂ�ƌ��������̂��낤�Ǝv���܂��B
�Ȃ��A�w�����A�ϕ��𖢗��C�̕��́A�w�����A�s��ϕ��A��ϕ��A�s��ϕ��̌������Q�Ƃ��Ă��������B
����āA�^���͎�����܂����B
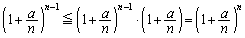 �@����A
�@����A�@���A
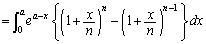 �@(���J�b�R����
�@(���J�b�R����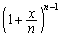 �ł�����܂�)
�ł�����܂�)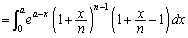
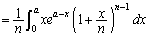
�� 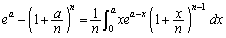 �@����B
�@����B
�E�ӂ̔�ϕ����́A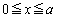 �ɂ����āA
�ɂ����āA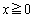 �C
�C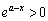 �C
�C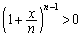 ���A
���A ����āA
�]���ćB���A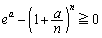 �@����C
�@����C
�A�C�C���A
(3) �ؖ����ׂ����̍��ӂ͇B�̍��ӂɏo�Ă��܂��B�B�̉E�ӂ�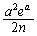 �ȉ��ł��邱�Ƃ������悢�킯�ł��B�B�̉E�ӂɊ���
�ȉ��ł��邱�Ƃ������悢�킯�ł��B�B�̉E�ӂɊ���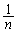 �����Ă���̂ŁA�ϕ���
�����Ă���̂ŁA�ϕ���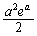 �ȉ��ł���悢�A�Ƃ������ƂɂȂ�܂��B
�ȉ��ł���悢�A�Ƃ������ƂɂȂ�܂��B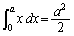 �Ȃ̂ŁA��ϕ����̎c��̕����ɂ��āA
�Ȃ̂ŁA��ϕ����̎c��̕����ɂ��āA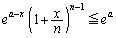 (�萔�ȉ��Ƃ����`�����)�����������̂ł����A(2)�ŁA
(�萔�ȉ��Ƃ����`�����)�����������̂ł����A(2)�ŁA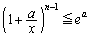 ��������Ă���̂ŁA
��������Ă���̂ŁA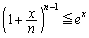 �C
�C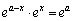 �ƂȂ�̂ʼn������܂��B���ǁA���Ă̗���͈ȉ��̂悤�ɂ���悢�ł��傤�B
�ƂȂ�̂ʼn������܂��B���ǁA���Ă̗���͈ȉ��̂悤�ɂ���悢�ł��傤�B 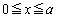 �ɂ����āA(2)���A
�ɂ����āA(2)���A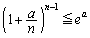 �Ȃ̂ŁA
�Ȃ̂ŁA���ӂ�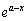 (
(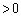 )�������āA
)�������āA ����āA�B�E�ӂ̔�ϕ����ɂ��āA
�� 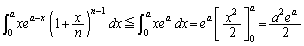 ���ӂ�
���ӂ�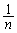 ��������A�B���A
��������A�B���A ����āA�^�s�����������܂����B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B