静岡大理数学'08年後期[5]
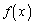 は区間
は区間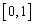 で定義された連続関数であり、
で定義された連続関数であり、
を満たすとする。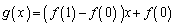 (
(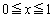 )とする。次の問いに答えよ。
)とする。次の問いに答えよ。
(1) 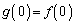 ,
,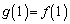 および
および が成り立つことを示し、さらに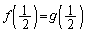 であることを示せ。
であることを示せ。 (2) nを自然数とし、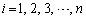 に対して、
に対して、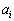 は0または1とする。次の等式を証明せよ。
は0または1とする。次の等式を証明せよ。 (3) 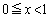 に対して
に対して とする。ただし、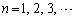 に対して、
に対して、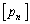 は
は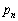 を越えない最大の整数を表す。このとき、
を越えない最大の整数を表す。このとき、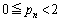 (
(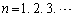 )および
)および であることを示せ。
(4) 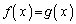 (
(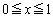 )であることを示せ。
)であることを示せ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 (2)も数学的帰納法の形にするのが難しいのですが、(3)はさらに難解です。
(1) ②において、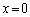 とすれば、
とすれば、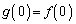
②において、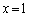 とすれば、
とすれば、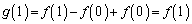
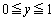 として、②のxをyとすれば、
として、②のxをyとすれば、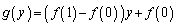 ・・・③
・・・③
②+③より、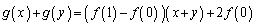
両辺を2で割り、 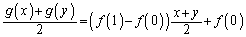 ・・・④
・・・④一方、②のxを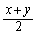 とすれば、
とすれば、 これと④より、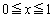 ,
,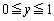 に対して、
に対して、 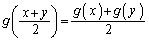 ・・・⑤
・・・⑤①において、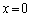 ,
,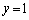 とすると、
とすると、 ⑤において、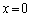 ,
,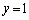 とすると、
とすると、 ∴ 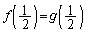
(2) 数学的帰納法だろう、という雰囲気は漂うのですが、問題は、どうやって、数学的帰納法の形にするか、ということです。(1)を使えば、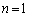 の場合は何とかなるでしょう。
の場合は何とかなるでしょう。 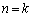 のとき、
のとき、が成り立つとして、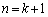 のときの等式
のときの等式 を導くのに、①,⑤を利用することになるだろう、ということは予測がつきます。ここで考えるべきことは、①,⑤のx,yを何にするか、ということです。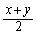 が出てくるので、
が出てくるので、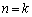 のときの形
のときの形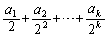 と何かを足して2で割ることになるでしょう。すると、
と何かを足して2で割ることになるでしょう。すると、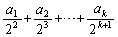 という形が出てきてしまいます。
という形が出てきてしまいます。
ここに出てくる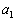 ,
,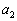 ,・・・,
,・・・,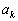 は、
は、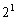 ,
,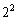 ,・・・,
,・・・,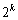 の分子、という意味ではありません。
の分子、という意味ではありません。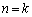 のときの
のときの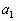 と
と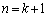 のときの
のときの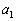 が同じものでなければならない、という制約もありません。それぞれ、0か1を表す、というだけのことです。であれば、
が同じものでなければならない、という制約もありません。それぞれ、0か1を表す、というだけのことです。であれば、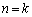 のときと、
のときと、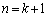 のときとで、
のときとで、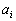 のiは同じ番号になっている必要はありません。
のiは同じ番号になっている必要はありません。
そこで、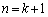 のときの形
のときの形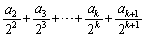 が出てくるように、
が出てくるように、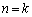 のときの形を、
のときの形を、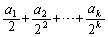 ではなく、番号を1つずらして、
ではなく、番号を1つずらして、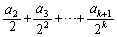 と書くことにします。これと
と書くことにします。これと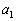 (0または1)を足して2で割ったものを
(0または1)を足して2で割ったものを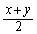 と考え、以下のようにします。
と考え、以下のようにします。 よって、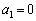 ,
,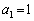 ,いずれの場合においても、
,いずれの場合においても、 が成立します。
(Ⅱ) 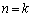 のとき、k個の文字
のとき、k個の文字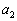 ,
,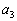 ,・・・,
,・・・,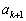 (項の番号に意味はありません)をそれぞれ0または1だとして、
(項の番号に意味はありません)をそれぞれ0または1だとして、 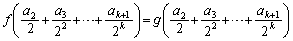 ・・・⑥
・・・⑥が成立すると仮定します。
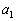 を0または1だとして、①,⑤のxを
を0または1だとして、①,⑤のxを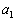 ,yを
,yを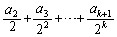 とすると、
とすると、 よって、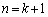 のときも成立します。
のときも成立します。 (Ⅰ),(Ⅱ)より、nを自然数として、
が成立します。
(3) ここも数学的帰納法だろう、ということはわかりますが、与えられた数列をどう料理するのか、何をすれば、 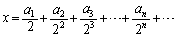 ・・・⑦
・・・⑦を示すことになるのか、見えてきません。ガウス記号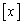 まで登場するのですが、まずは、問題文の
まで登場するのですが、まずは、問題文の 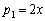 ,
,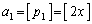
から出発します。では、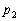 ,
,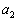 ではどのようになるでしょうか?
ではどのようになるでしょうか? Aを整数、Bを実数だとして、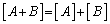 なので、
なので、 です。続けていくと、
などとなるので、
となることが予想できます。これを数学的帰納法で導くようにします。また、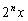 という形が出てくるので、⑦に
という形が出てくるので、⑦に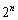 をかけてみると、
をかけてみると、 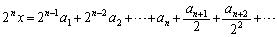 ・・・⑧
・・・⑧となりますが、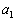 ,
,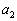 ,・・・,
,・・・,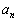 ,
,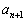 ,
,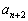 ,・・・ は、それぞれ0または1です。また、
,・・・ は、それぞれ0または1です。また、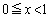 より、すべての自然数iについて
より、すべての自然数iについて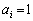 となることはないのです。すべての自然数iについて
となることはないのです。すべての自然数iについて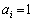 なら、初項
なら、初項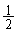 ,公比
,公比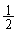 の無限等比級数の和が
の無限等比級数の和が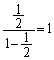 となることから、
となることから、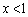 に反します。
に反します。
よって、数列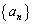 の中には、
の中には、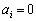 となる項があります。
となる項があります。
同様に、あるjについて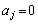 で、
で、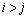 となるすべての自然数iについて
となるすべての自然数iについて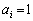 だとすれば、これは、
だとすれば、これは、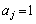 で、
で、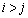 となるすべての自然数iについて
となるすべての自然数iについて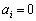 であることと同じです。
であることと同じです。
従って、⑧の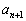 ,
,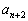 ,・・・ の中には0になるものがあり、
,・・・ の中には0になるものがあり、 つまり、
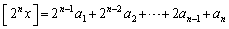 ・・・⑨
・・・⑨ここで、指数と項番号を1ずつずらすと、
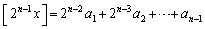 ・・・⑩
・・・⑩⑨−⑩×2より、
これで、先に予想した形が出てきます。これで、この設問の枠組みが見えてきました。
問題文の漸化式で与えられる数列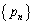 ,
,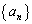 について、数学的帰納法により、
について、数学的帰納法により、 であることを示します。
(Ⅰ) 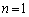 のとき、
のとき、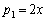 ですが、
ですが、 ⑪で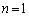 とすると、
とすると、 となります。
また、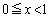 より
より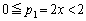 です。
です。
また、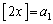
よって、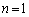 のとき成立します。
のとき成立します。 (Ⅱ) 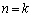 のとき、⑪,⑫,
のとき、⑪,⑫,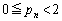 ,⑬が成立すると仮定します。
,⑬が成立すると仮定します。 です。
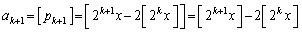 ・・・⑮
・・・⑮⑭,⑮より、
よって、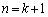 のときにも成立します。
のときにも成立します。 (Ⅰ),(Ⅱ)より、すべての自然数nについて、⑪,⑫,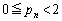 ,⑬が示せました。
,⑬が示せました。
⑬より、 “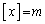 (m:整数) ⇔
(m:整数) ⇔ 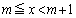 ”より、
”より、 ∴ 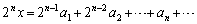
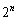 で割って、
で割って、 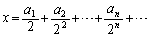 (nがすべての自然数であることに注意)
(nがすべての自然数であることに注意)
(4) 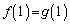 と、
と、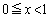 をみたす任意のxについて、(3)より、
をみたす任意のxについて、(3)より、 の形に表せば、(2)より、
よって、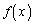 が連続な関数であることから、
が連続な関数であることから、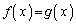
追記.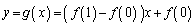 は、曲線
は、曲線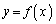 上の2点
上の2点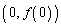 ,
,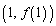 を通過する直線の方程式です。
を通過する直線の方程式です。
曲線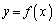 上の2点
上の2点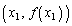 ,
,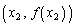 を通過する直線の傾きは
を通過する直線の傾きは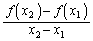 です。
です。
曲線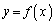 上の2点
上の2点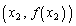 ,
,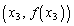 を通過する直線の傾きは
を通過する直線の傾きは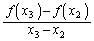 です。
です。
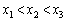 だとして、曲線
だとして、曲線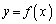 上の2点を通過する直線の傾きが増加するとき、つまり、
上の2点を通過する直線の傾きが増加するとき、つまり、
であるとき、曲線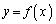 は「下に凸」である、と言います。このとき、
は「下に凸」である、と言います。このとき、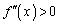 であることが平均値の定理を使って証明できます(曲線の凹凸を参照)。曲線
であることが平均値の定理を使って証明できます(曲線の凹凸を参照)。曲線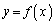 上の2点を通過する直線の傾きが減少するとき、つまり、
上の2点を通過する直線の傾きが減少するとき、つまり、
である場合には、曲線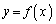 は「上に凸」である、と言います。このときは
は「上に凸」である、と言います。このときは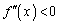 です。
です。
ここで、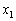 がx,
がx,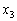 がy,
がy,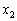 が
が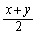 だとすると、
だとすると、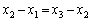 なので、曲線
なので、曲線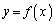 が下に凸であれば、
が下に凸であれば、
となり、
が成立します。この不等式は、下に凸な曲線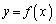 上の点
上の点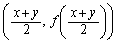 は、この点の両側に位置する曲線上の2点
は、この点の両側に位置する曲線上の2点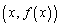 ,
,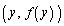 の中点
の中点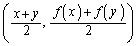 よりも下にある、ということを意味しています(図に描いてみれば明らかです)。
よりも下にある、ということを意味しています(図に描いてみれば明らかです)。
同様に、上に凸な曲線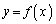 上の点
上の点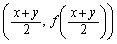 は、この点の両側に位置する曲線上の2点
は、この点の両側に位置する曲線上の2点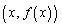 ,
,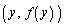 の中点
の中点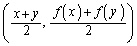 よりも上にあります。この事実は、証明問題などに応用できます(阪大理系'07年前期[2]を参照)。
よりも上にあります。この事実は、証明問題などに応用できます(阪大理系'07年前期[2]を参照)。
本問では、
だと言っているのですが、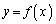 がx,yの存在範囲においては直線的になっていることを意味しています。本問は、結局、直線上の2点を結ぶ直線上の点は、もとの直線上の点になっている、つまり、
がx,yの存在範囲においては直線的になっていることを意味しています。本問は、結局、直線上の2点を結ぶ直線上の点は、もとの直線上の点になっている、つまり、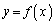 と
と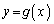 は同じ直線になる、ということを言っています。自明のことかも知れませんが、(3)では、2分法(2点の中点を考え、さらに、元の点と中点のそのまた中点を考えていく)のアルゴリズムを数列を使って一般的に考えようとしているので、難解な問題になっています。
は同じ直線になる、ということを言っています。自明のことかも知れませんが、(3)では、2分法(2点の中点を考え、さらに、元の点と中点のそのまた中点を考えていく)のアルゴリズムを数列を使って一般的に考えようとしているので、難解な問題になっています。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 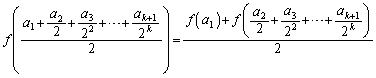
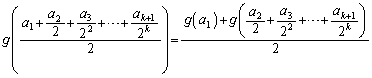
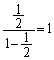 となることから、
となることから、