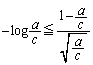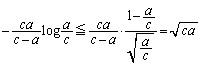��嗝�n���w'07�N�O��[2]
���̖₢�ɓ�����B
(1) x�����̐��̂Ƃ�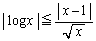 �������B
�������B (2) p�Cq�Cr��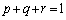 �������̐��̂Ƃ�
�������̐��̂Ƃ� �������B
�������B (3) a�Cb�Cc�����قȂ鐳�̐���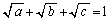 �����Ƃ�
�����Ƃ� �������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�U���ʂ�ɂ���čs���ł��܂����A�S���ʂ̃A�v���[�`�ł��\�Ȃ̂ʼn��L�́u�NjL�v�ŏЉ�܂��B
(1) ��Βl�������܂܂ł͂��ɂ����̂ŁA��Βl�L�����̐����ŕ����čl���邱�Ƃɂ��܂��B
 �ƂȂ�̂́A
�ƂȂ�̂́A �̂Ƃ��ł��B
�̂Ƃ��ł��B
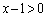 �ƂȂ�̂��A
�ƂȂ�̂��A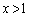 �̂Ƃ��ł��B
�̂Ƃ��ł��B
�����ŁA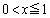 �̂Ƃ���
�̂Ƃ��� �̂Ƃ��Ƃŕ����Ē��ׂ邱�Ƃɂ��܂��B
�̂Ƃ��Ƃŕ����Ē��ׂ邱�Ƃɂ��܂��B
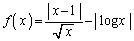 �Ƃ����܂��B
�Ƃ����܂��B(i) 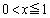 �̂Ƃ��A
�̂Ƃ��A ����āA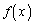 �͌������ŁA
�͌������ŁA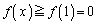 �@(���̑������Q��)��
�@(���̑������Q��)��  �@����@
�@����@ (ii) 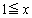 �̂Ƃ��A
�̂Ƃ��A ����āA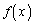 �͑������ŁA
�͑������ŁA
�� 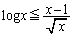 �@����A
�@����A �@�C�A���Ax�����̐��̂Ƃ�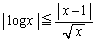 �ƂȂ�܂��B
�ƂȂ�܂��B
(2) �Z�I���g���܂ł��Ȃ��Ǝv���܂��B
 �C
�C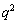 �C
�C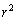 ���o�Ă���̂ŁA
���o�Ă���̂ŁA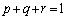 �̗��ӂ�2�悵�āA
�̗��ӂ�2�悵�āA�� 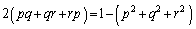 �@����B
�@����B 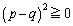 ���A
���A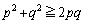 �@����C
�@����C
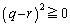 ���A
���A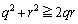 �@����D
�@����D
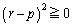 ���A
���A �@����E
�@����E�C�{�D�{�E���A
���̉E�ӂ��B��p���ď���������ƁA
��  ���D��L�ł́A�������ρA���敽�ς̊W(�s�����̏ؖ����Q��)���g�����Ƃ�������̂ŁAp�Cq�Cr�̒��ɕ����������Ă��A�^�s�����͐������܂��B
���D��L�ł́A�������ρA���敽�ς̊W(�s�����̏ؖ����Q��)���g�����Ƃ�������̂ŁAp�Cq�Cr�̒��ɕ����������Ă��A�^�s�����͐������܂��B
(3) a�Cb�Cc�͑��قȂ�̂ŁA �Ƃ��Ĉ�ʐ��������܂���(���̏ꍇ�ł��A3���̒��̍ŏ��̂��̂�a�C�ő�̂��̂�c�C�c���b�Ɠ���ւ��čl�����OK)�B
�Ƃ��Ĉ�ʐ��������܂���(���̏ꍇ�ł��A3���̒��̍ŏ��̂��̂�a�C�ő�̂��̂�c�C�c���b�Ɠ���ւ��čl�����OK)�B (1)�Ŏ������s�����ɂ����āA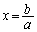 �Ƃ���ƁA
�Ƃ���ƁA ���A
���A ���ӂ�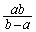 (
( )��������ƁA
)��������ƁA  �@����F
�@����F���l�ɂ��āA(1)�̕s������ (
( )�Ƃ��邱�Ƃɂ��A
)�Ƃ��邱�Ƃɂ��A  �@����G
�@����G(1)�̕s�����ŁA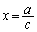 �Ƃ���ƁA
�Ƃ���ƁA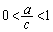 ���A
���A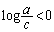 �ɒ��ӂ��āA
�ɒ��ӂ��āA ���ӂ� (
(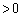 )��������ƁA
)��������ƁA ���ӂ��A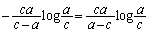 �Ƃ��āA
�Ƃ��āA 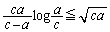 �@����H
�@����H�F�{�G�{�H���A
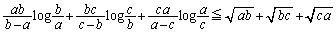 �@����I
�@����I���̉E�ӂׂ邽�߂ɁA(2)�Ɠ��l�A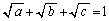 �̗��ӂ�2�悵�܂��B
�̗��ӂ�2�悵�܂��B (2)�̌��ʂ��A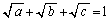 �̂Ƃ��A
�̂Ƃ��A �ł����A
�ł����A �� 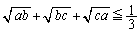 �I���A
�I���A
�NjL�D(1)�̕s�����ɐ�Βl�L�������Ă���̂ŁA(3)�̓��Ăł́A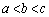 �Ɖ��肹���ɁA�u(1)�ɂ����āA
�Ɖ��肹���ɁA�u(1)�ɂ����āA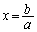 �C
�C �C
�C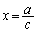 �Ƃ��āA�F�C�G�C�H��������v�Ƃ��������Ă����̂������ł��傤�B
�Ƃ��āA�F�C�G�C�H��������v�Ƃ��������Ă����̂������ł��傤�B
���̖��̂悤�ɕ����������o�Ă���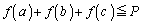 �̂悤�Ȍ`�̕s�����̏ؖ����ŗL���ȋZ�I�Ƃ��āA���̉����ɒ��ڂ���A�Ƃ������̂�����܂��B�y���ł��ċ��͂Ȃ̂Őg�ɂ��Ă��������Z�I�ł��B�����@�̕s�����ւ̉��p(2)���A3�ȏ�̕����Ɋւ��鑊�����ρE���敽�ς̊W�ȂǁA�d�v�ȗ���Љ�Ă���̂ł��ЎQ�Ƃ��Ă��������B
�̂悤�Ȍ`�̕s�����̏ؖ����ŗL���ȋZ�I�Ƃ��āA���̉����ɒ��ڂ���A�Ƃ������̂�����܂��B�y���ł��ċ��͂Ȃ̂Őg�ɂ��Ă��������Z�I�ł��B�����@�̕s�����ւ̉��p(2)���A3�ȏ�̕����Ɋւ��鑊�����ρE���敽�ς̊W�ȂǁA�d�v�ȗ���Љ�Ă���̂ł��ЎQ�Ƃ��Ă��������B
���̖���(2)�ł���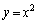 �̉��ʂ𗘗p�����ؖ����l�����܂��B�Ȑ�
�̉��ʂ𗘗p�����ؖ����l�����܂��B�Ȑ�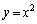 �́A
�́A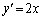 �C
�C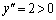 �ʼn��ɓʁA�Ȑ���̂ǂ̓_���ڐ����l���Ă��A�Ȑ��͐ڐ������ɗ��܂��B
�ʼn��ɓʁA�Ȑ���̂ǂ̓_���ڐ����l���Ă��A�Ȑ��͐ڐ������ɗ��܂��B
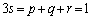 (
(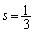 )�Ƃ��āA
)�Ƃ��āA �ɂ�����ڐ��́A
�ɂ�����ڐ��́A
�Ȑ���̓_ �C
�C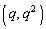 �C
�C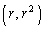 �͐ڐ������ɗ���̂ŁA
�͐ڐ������ɗ���̂ŁA
�@�{�A�{�B���A
�ƂȂ�܂��B
���̖���(3)�́A(1)�����͂ȃq���g�ɂȂ��Ă���̂�(1)�𗘗p���ē�����悢�̂ł����A����(3)�������Ȃ�o�Ă����悤�ȏꍇ�A��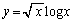 �̉��ʂ𗘗p���邱�Ƃ��ł��܂��B
�̉��ʂ𗘗p���邱�Ƃ��ł��܂��B
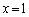 �ɂ�����ڐ��́A
�ɂ�����ڐ��́A �̂Ƃ�
�̂Ƃ� �C
�C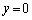 ���A
���A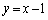 �@����D
�@����D
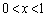 �ɂ�����
�ɂ�����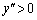 ���A�Ȑ�
���A�Ȑ� �͐ڐ������ɗ��܂��B
�͐ڐ������ɗ��܂��B
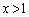 �ɂ�����
�ɂ����� ���A�Ȑ�
���A�Ȑ� �͐ڐ����牺�ɗ��܂��B
�͐ڐ����牺�ɗ��܂��B
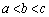 �Ƃ��āA�Ȑ���̓_
�Ƃ��āA�Ȑ���̓_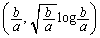 ��
��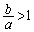 ���ڐ��D��艺�ɗ���̂ŁA
���ڐ��D��艺�ɗ���̂ŁA
���ӂ�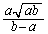 (
(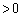 )�������āA
)�������āA
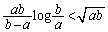 �@����E
�@����E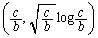 ��
��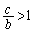 ���ڐ��D��艺�ɗ���̂ŁA
���ڐ��D��艺�ɗ���̂ŁA
���ӂ� (
( )�������āA
)�������āA
 �@����F
�@����F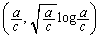 ��
��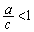 ���ڐ��D����ɗ���̂ŁA
���ڐ��D����ɗ���̂ŁA
���ӂ�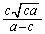 (
(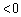 )��������(�s�����̌������ς��܂�)�A
)��������(�s�����̌������ς��܂�)�A
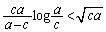 �@����G
�@����G
���Ƃ͏�L�̉Ɠ������A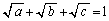 ���
���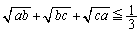 ���A
���A
�ƂȂ�܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 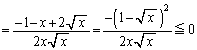
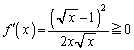
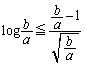
 �@����F
�@����F