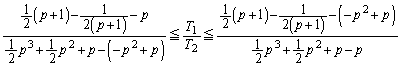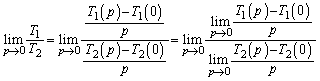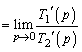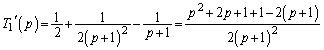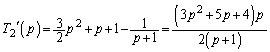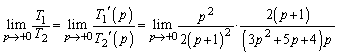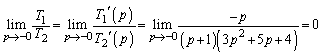防衛医大数学'09年[1]
曲線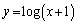 上の点P
上の点P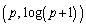 における接線と法線をそれぞれ
における接線と法線をそれぞれ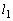 ,
,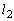 とする。曲線と接線
とする。曲線と接線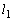 とy軸で囲まれる部分の面積を
とy軸で囲まれる部分の面積を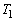 ,曲線と法線
,曲線と法線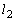 とy軸で囲まれる部分の面積を
とy軸で囲まれる部分の面積を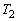 とする。ただし、
とする。ただし、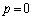 のとき、
のとき、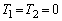 とおく。
とおく。
このとき、以下の問いに答えよ。
(1) 接線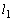 と法線
と法線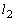 の方程式を求めよ。
の方程式を求めよ。 (2) 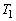 ,
,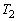 をpを用いて表せ。
をpを用いて表せ。 (3) 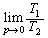 を求めよ。
を求めよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 (1),(2)は標準問題ですが、(3)の極限を求めるところで苦労させられます。接線と法線については、接線と法線の公式、面積計算については、定積分と面積(その2)を参照してください。
(1) 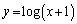
 :
: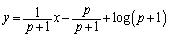 ......[答]
......[答] :
: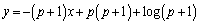 ......[答]
......[答]
(2) 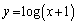 は
は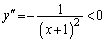 より上に凸な曲線で、接線
より上に凸な曲線で、接線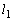 は曲線
は曲線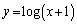 から上に来ます。
から上に来ます。 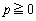 のとき、
のとき、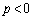 のとき、
のとき、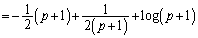 ......[答]
......[答]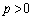 のとき、
のとき、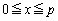 において法線
において法線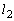 は曲線
は曲線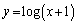 から上に来ます。
から上に来ます。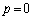 のときを含め
のときを含め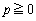 のとき、
のとき、結局、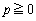 ,
,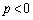 ,いずれであっても、
,いずれであっても、 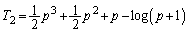 ......[答]
......[答]
(3) 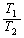 の極限は、
の極限は、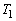 ,
,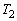 の形が悪いので、はさみうちに持ち込むことが考えられます。
の形が悪いので、はさみうちに持ち込むことが考えられます。 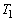 ,
,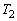 の中に
の中に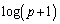 が出てきますが、例えば、
が出てきますが、例えば、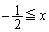 において成立する不等式:
において成立する不等式:を利用して、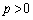 のとき、
のとき、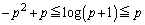 より、
より、 としても、
となり、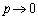 のときに左辺と右辺が同じ値に収束してくれません。この考え方では、はさみうちの左辺と右辺が同じ値に収束する形を作るのが難しく、なかなかうまく行きません(この方法での解答は旺文社全国大学入試問題正解を参照してください)。
のときに左辺と右辺が同じ値に収束してくれません。この考え方では、はさみうちの左辺と右辺が同じ値に収束する形を作るのが難しく、なかなかうまく行きません(この方法での解答は旺文社全国大学入試問題正解を参照してください)。
そこで、ロピタルの定理に頼ることになるのですが、ロピタルの定理は高校数学の教科書に登場しないので、証明なしで用いてもよいのか不安です。
本問では、問題文でわざわざ、「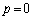 のとき、
のとき、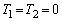 とおく」と指定されているので、以下のようにして、「ロピタルの定理より」という言い方を回避することができます。pの関数
とおく」と指定されているので、以下のようにして、「ロピタルの定理より」という言い方を回避することができます。pの関数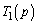 ,
,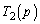 において、
において、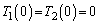 より、
より、 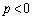 のときは、
のときは、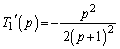
∴ 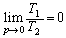 ......[答]
......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。