���u�Б嗝�H���w'09�N[4]
�o�Ȑ�C�F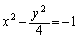 �ɂ��Ď��̖₢�ɓ�����B
�ɂ��Ď��̖₢�ɓ�����B
(1) C�̑Q�ߐ��̕��������L���B
(2) m��C�ӂ̎����Ƃ��āA����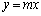 ���Ȑ�C�ɐڂ��Ă��Ȃ����Ƃ������B
���Ȑ�C�ɐڂ��Ă��Ȃ����Ƃ������B (3) �_A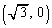 ��ʂ�C�̐ڐ��̕����������ׂċ��߂�B
��ʂ�C�̐ڐ��̕����������ׂċ��߂�B (4) C��ɂȂ��_P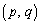 ��ʂ�C�̐ڐ������傤��2�{�����āA2�{�̐ڐ�����������Ƃ��Ap�Cq���݂����ׂ����������߂�B
��ʂ�C�̐ڐ������傤��2�{�����āA2�{�̐ڐ�����������Ƃ��Ap�Cq���݂����ׂ����������߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�ȉ~�F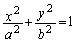 �̒���2�ڐ��̌�_�̋O�Ղ͏��~�ƌĂ��~�F
�̒���2�ڐ��̌�_�̋O�Ղ͏��~�ƌĂ��~�F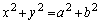 �ɂȂ邱�Ƃ��悭�m���Ă��ē����ł��p�o�ł����A�o�Ȑ��ł͂ǂ����A�Ƃ������ł��B
�ɂȂ邱�Ƃ��悭�m���Ă��ē����ł��p�o�ł����A�o�Ȑ��ł͂ǂ����A�Ƃ������ł��B
�́A�E�}���F�����̂悤�ɁAx�����͂���ŁA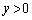 �̕�����
�̕�����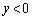 �̕����ɕ�����Ă���Ȑ��ł�(���F�̒����͑Q�ߐ�)�B
�̕����ɕ�����Ă���Ȑ��ł�(���F�̒����͑Q�ߐ�)�B
(1) C�̑Q�ߐ��́AC�̕������@�̉E�ӂ�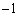 ��0�ɂ��邱�Ƃɂ���ē����܂��B
��0�ɂ��邱�Ƃɂ���ē����܂��B 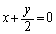 �C
�C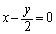 ......[��]
......[��]
(2) 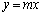 �@����A
�@����A �@�C�A��A����y���������āA
�� 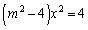 �@����B
�@����B
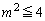 �̂Ƃ��ɂ́A�B����x�͑��݂��܂���B�܂�A�����A��C�Ɛړ_����_�������܂���B
�̂Ƃ��ɂ́A�B����x�͑��݂��܂���B�܂�A�����A��C�Ɛړ_����_�������܂���B
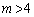 �̂Ƃ��ɂ́A
�̂Ƃ��ɂ́A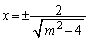 �ƂȂ�A����͏d���ł͂Ȃ��̂ŁA�����A��C��2��_�������܂�(�O���t�Ŋm�F���Ă�������)�B
�ƂȂ�A����͏d���ł͂Ȃ��̂ŁA�����A��C��2��_�������܂�(�O���t�Ŋm�F���Ă�������)�B
����āA����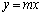 ���Ȑ�C�ɐڂ��邱�Ƃ͂���܂���B
���Ȑ�C�ɐڂ��邱�Ƃ͂���܂���B
(3) A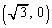 ��ʂ�x���ɐ�����C�̐ڐ��͂���܂���B�����ŁA�X����m�Ƃ��āAA��ʂ钼�����A
��ʂ�x���ɐ�����C�̐ڐ��͂���܂���B�����ŁA�X����m�Ƃ��āAA��ʂ钼�����A 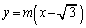 �@����C
�@����C�Ƃ����āA�@�ƘA�����܂��B
����́A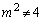 �̂Ƃ���x��2���������ɂȂ�܂��BC�ƇC�͐ڂ���̂ŁA����2���������͏d���������܂��B���ʎ�
�̂Ƃ���x��2���������ɂȂ�܂��BC�ƇC�͐ڂ���̂ŁA����2���������͏d���������܂��B���ʎ�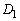 �ɂ��āA
�ɂ��āA �� 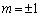 �@(
�@(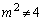 �����܂�)�C���AA��ʂ�ڐ��́A
�����܂�)�C���AA��ʂ�ڐ��́A 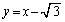 �C
�C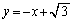 ......[��]
......[��]
(4) �v�Z�̎�Ԃ͂قƂ�Ǖς��Ȃ��̂ŁA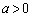 �C
�C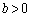 ��p���āA�o�Ȑ����A
��p���āA�o�Ȑ����A 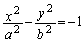 �@����D
�@����D�Ƃ��Čv�Z���邱�Ƃɂ��܂��B�{��ł́A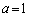 �C
�C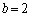 �ł��BP
�ł��BP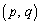 ��ʂ�x���ɐ����ȇD�̐ڐ��͂���܂���B�����ŁA�X����m�Ƃ��āAP��ʂ钼�����A
��ʂ�x���ɐ����ȇD�̐ڐ��͂���܂���B�����ŁA�X����m�Ƃ��āAP��ʂ钼�����A 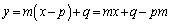 �@����E
�@����E�Ƃ����āA�D�ƘA�����܂��B
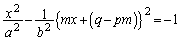 �@(�ȉ��A
�@(�ȉ��A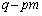 ���ЂƂ�����ɂ��Čv�Z����̂��R�c�ł�)
���ЂƂ�����ɂ��Čv�Z����̂��R�c�ł�)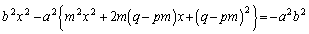
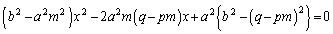
����́A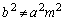 �̂Ƃ���x��2���������ɂȂ�܂��B
�̂Ƃ���x��2���������ɂȂ�܂��B
�D�ƇE�͐ڂ���̂ŁA����2���������͏d���������܂��B���ʎ�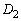 �ɂ��āA
�ɂ��āA �F��m�Ɋւ���2���������ƌ���ƁA2����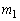 �C
�C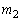 �Ƃ��āA2�ڐ��͒�������̂ŁA���ƌW���̊W��p���āA
�Ƃ��āA2�ڐ��͒�������̂ŁA���ƌW���̊W��p���āA �� 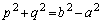 �@����G
�@����G
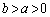 �ł���A�����P
�ł���A�����P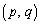 �����_�𒆐S�Ƃ��A���a
�����_�𒆐S�Ƃ��A���a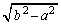 �̉~����̓_�ł��邱�Ƃ��Ӗ����A�ȉ~�̏ꍇ�ɑΉ����錋�ʂƂȂ�܂��B
�̉~����̓_�ł��邱�Ƃ��Ӗ����A�ȉ~�̏ꍇ�ɑΉ����錋�ʂƂȂ�܂��B
�Ƃ���ŁA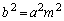 �C
�C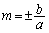 �C�܂�A�������Q�ߐ��ɕ��s�ɂȂ�Ƃ��ɂ́A�����́A�o�Ȑ���1��_�������A��_�������Ȃ����̂����ꂩ�ŁA�ڂ��邱�Ƃ͂���܂���B
�C�܂�A�������Q�ߐ��ɕ��s�ɂȂ�Ƃ��ɂ́A�����́A�o�Ȑ���1��_�������A��_�������Ȃ����̂����ꂩ�ŁA�ڂ��邱�Ƃ͂���܂���B
�F��m��2���������ƌ���Ƃ��A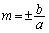 �����ɂ��ĂȂ��̂ŁA
�����ɂ��ĂȂ��̂ŁA �� 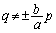 �@����H
�@����H
�{��ł́A�G�C�H�ɂ�����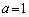 �C
�C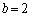 �Ƃ��āA
�Ƃ��āA 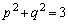 ����
���� 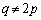 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B