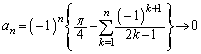�k�嗝�n���w'09�N�O��[5]
���R��n�ɑ���
�Ƃ����B���̂Ƃ��A�ȉ��̖₢�ɓ�����B
(1)  �����߂�B
�����߂�B (2) 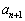 ��
��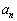 �ŕ\���B
�ŕ\���B (3)  �����߂�B
�����߂�B (4) 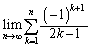 �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@��ϕ��̑Q�����́A�����ϕ��Ɏ������ނ̂���ł����A �����́A
�����́A
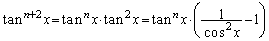
�𗘗p����̂Œ��ӂ��Ă��������B
(2)�œ�����Q�����ŁA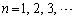 �Ƃ��Ă݂�A(4)�̌`�������Ă��āA�S�̂̃X�g�[���[�����n���܂��B
�Ƃ��Ă݂�A(4)�̌`�������Ă��āA�S�̂̃X�g�[���[�����n���܂��B
(2) 
�� 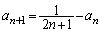 ......[��]
......[��]
(3) (2)�œ���ꂽ�Q�����ŁA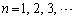 �Ƃ��čs���ƁA
�Ƃ��čs���ƁA �ƂȂ�A(4)�̌`�������Ă���̂ŁA(3)��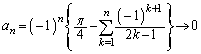 �Ƃ���āA�Ō�́A
�Ƃ���āA�Ō�́A �Ƃ���̂��낤�A�Ƃ����A���̖��̃X�g�[���[�����n���܂��B
�Ƃ���̂��낤�A�Ƃ����A���̖��̃X�g�[���[�����n���܂��B
�@�̌`�ł́A �̂Ƃ�
�̂Ƃ�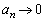 �������̂͑�ςł��B
�������̂͑�ςł��B
�����ŁA���̒�ϕ��̌`�����邱�ƂɂȂ�܂����A��ϕ����� �����炩�̕s�����ł͂��ނ̂��낤�A�Ƃ����A�C�f�A���N���܂��B
�����炩�̕s�����ł͂��ނ̂��낤�A�Ƃ����A�C�f�A���N���܂��B
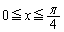 �ɂ�����
�ɂ�����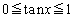 �Ȃ̂ŁA
�Ȃ̂ŁA �ł��B
�ł��B
�e�ӂɐϕ��L��������ƁA���ׂĂ̎��R��n�ɂ��āA 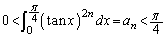 �@����A
�@����A(2)�̕s�����𗘗p����ƁA ���A
���A ��  ������
������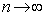 �Ƃ���ƁA
�Ƃ���ƁA �Ȃ̂ŁA�͂��݂����̌������A
�Ȃ̂ŁA�͂��݂����̌������A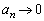
��  ......[��]���D�A��
......[��]���D�A��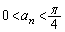 �����ł́A
�����ł́A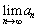 ���������邱�Ƃ͂킩��܂����A�Ɍ��l���킩��܂���B
���������邱�Ƃ͂킩��܂����A�Ɍ��l���킩��܂���B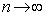 �̂Ƃ���0�Ɏ���������̂������Ă��ďォ��}���Ă��K�v������܂��B
�̂Ƃ���0�Ɏ���������̂������Ă��ďォ��}���Ă��K�v������܂��B
 �̃O���t��
�̃O���t�� ��ʂ�A
��ʂ�A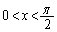 �ɂ����ĉ��ɓʂł��邱�Ƃ𗘗p����ƁA
�ɂ����ĉ��ɓʂł��邱�Ƃ𗘗p����ƁA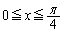 �ɂ�����
�ɂ����� �Ƃ����s�����������܂��B������A
�Ƃ����s�����������܂��B������A ����������A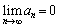 �������܂��B
�������܂��B
(�T)  �̂Ƃ��A�B�ɂ����āA
�̂Ƃ��A�B�ɂ����āA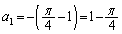 �ƂȂ�܂����A(1)�̌��ʂ�萬�藧���܂��B
�ƂȂ�܂����A(1)�̌��ʂ�萬�藧���܂��B (�U)  �̂Ƃ��A�B�����藧�Ɖ��肷��ƁA
�̂Ƃ��A�B�����藧�Ɖ��肷��ƁA (2)�̑Q������p���āA
����āA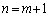 �̂Ƃ��ɂ��A�B���������܂��B
�̂Ƃ��ɂ��A�B���������܂��B (�T)�C(�U)���A���ׂĂ̎��R��n�ɂ��āA�B�����藧���܂��B(3)���A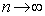 �̂Ƃ��A
�̂Ƃ��A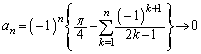
�� 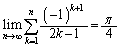 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 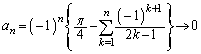 �Ƃ���āA�Ō�́A
�Ƃ���āA�Ō�́A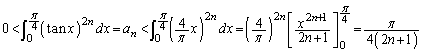

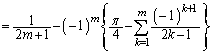

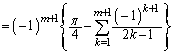 �@(k�̏�[�̒l�ɒ���)
�@(k�̏�[�̒l�ɒ���)