�L���嗝�n���w'09�N[3]
�Ȑ�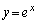 ��̓_A
��̓_A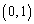 �ɂ�����ڐ���
�ɂ�����ڐ���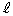 �Ƃ��A�_B
�Ƃ��A�_B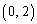 ��ʂ蒼��
��ʂ蒼��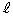 �ɕ��s�Ȓ�����m�Ƃ���B����m�ƋȐ�
�ɕ��s�Ȓ�����m�Ƃ���B����m�ƋȐ�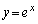 ��2�̌�_P�CQ��x���W�����ꂼ��α�Cβ (������
��2�̌�_P�CQ��x���W�����ꂼ��α�Cβ (������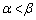 )�Ƃ���B����
)�Ƃ���B����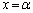 �ƒ���
�ƒ���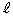 �̌�_��
�̌�_��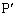 �C����
�C����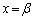 �ƒ���
�ƒ���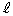 �̌�_��
�̌�_��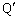 �Ƃ���B���̖₢�ɓ�����B
�Ƃ���B���̖₢�ɓ�����B
(1) ���s�l�ӌ`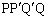 �̖ʐ�S��α�Cβ �ŕ\���B
�̖ʐ�S��α�Cβ �ŕ\���B (2) ����m�ƋȐ�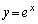 �ɂ���Ĉ͂܂��}�`�̖ʐ�T��α�Cβ�̑������ŕ\���B
�ɂ���Ĉ͂܂��}�`�̖ʐ�T��α�Cβ�̑������ŕ\���B (3) ����PQ�̒��_R�͑�2�ی��ɂ��邱�Ƃ������B
(4) 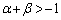 �ł��邱�Ƃ������B
�ł��邱�Ƃ������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�s�����̏ؖ����Ȑ��̉����𗘗p����A�Ƃ����Z�I���m���Ă��܂����A���X�A�����W���ĉ��ʂ��l���Ă݂悤�A�Ƃ������ł��B
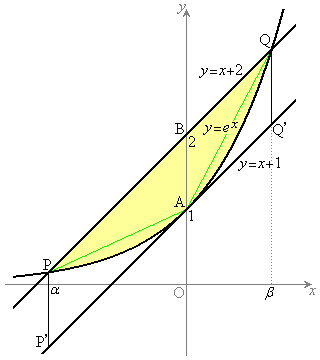 (1)
(1) 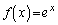 �Ƃ��܂��B
�Ƃ��܂��B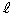 �F
�F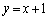
�����ŁA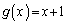 �Ƃ��܂��B���l�ɁAB
�Ƃ��܂��B���l�ɁAB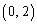 ��ʂ�
��ʂ�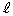 �ɕ��s�������́A
�ɕ��s�������́A m�F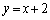
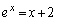 �@����@
�@����@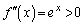 ��
��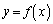 �̃O���t�͉��ɓʂȂ̂ŁA�E�}���A�������@�͑��قȂ�2�������������܂��B��ӂ��A���������̉���α�ő傫�����̉���β �ł��B�]���āA
�̃O���t�͉��ɓʂȂ̂ŁA�E�}���A�������@�͑��قȂ�2�������������܂��B��ӂ��A���������̉���α�ő傫�����̉���β �ł��B�]���āA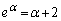 �C
�C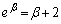 �@����A
�@����A�����藧���܂��B
����m�͒���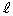 ��y����������1���s�ړ������������Ȃ̂ŁA���s�l�ӌ`
��y����������1���s�ړ������������Ȃ̂ŁA���s�l�ӌ`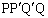 �́A��ӂ̒���1�C����
�́A��ӂ̒���1�C����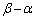 �̕��s�l�ӌ`�ŁA���̖ʐ�S�́A
�̕��s�l�ӌ`�ŁA���̖ʐ�S�́A 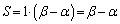 ......[��]
......[��]
�A��p���āA
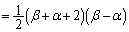 ......[��]
......[��]
(3)(4) �_P�C�_Q��y���W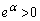 �C
�C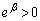 ���A����PQ�̒��_R����2�ی��ɂ���A�Ƃ������Ƃ́AR��x���W
���A����PQ�̒��_R����2�ی��ɂ���A�Ƃ������Ƃ́AR��x���W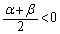 �Ƃ������Ƃł��B(4)��
�Ƃ������Ƃł��B(4)��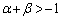 �ƍ��킹�āA
�ƍ��킹�āA 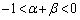 �@����B
�@����B�������悢�킯�ł��B
�����������ŕs�����̏ؖ�������ꍇ�ɁA�Ȑ��̉��ʂɒ��ڂ���Ƃ��܂��s���ꍇ������܂��B
���ɓʂȋȐ�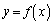 ��̓_�͂��̐ڐ�
��̓_�͂��̐ڐ�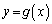 �����ɗ���̂ŁA�_P�C�_Q�ɒ��ڂ���ƁA
�����ɗ���̂ŁA�_P�C�_Q�ɒ��ڂ���ƁA 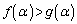 �C
�C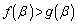
���A
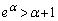 �C
�C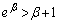 �@����C
�@����C�Ƃ����s�������ł��܂��B
�܂��A���ɓʂȋȐ�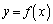 ���2�_PQ�����Ԑ���
���2�_PQ�����Ԑ���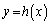 (
(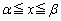 )��̓_�́A�Ȑ�
)��̓_�́A�Ȑ�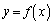 �����ɗ���̂ŁAPQ�̒��_
�����ɗ���̂ŁAPQ�̒��_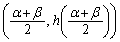 �ɂ��āA
�ɂ��āA �ƇA���A
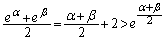 �@����D�@(
�@����D�@(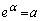 �C
�C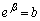 �Ƃ����A�������ρE���敽�ς̊W�F
�Ƃ����A�������ρE���敽�ς̊W�F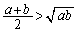 �������܂�)
�������܂�)�Ƃ����s�������ł��܂��B�ł����A�C�C�D����B���o�����Ƃ��ł��܂���B�{��ł́A���ʂɒ��ڂ��邾���ł́A�B�����Â��s�������������Ȃ��̂ł��B�����ŁA(1)�C(2)�ōl�����ʐς𗘗p���āA�Ȑ��̉��ʂ̋�������ƌ������]������A�Ƃ����̂���ӂł��B(1)�C(2)���g���ƁA�Ȑ�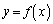 �̋Ȃ����ɂ��āA����m�F
�̋Ȃ����ɂ��āA����m�F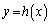 �ƋȐ�
�ƋȐ�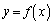 �Ƃň͂܂�镔���̖ʐ�T�����s�l�ӌ`
�Ƃň͂܂�镔���̖ʐ�T�����s�l�ӌ`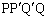 �̖ʐ�S�����������Ƃ����s��������邱�Ƃ��ł��܂��B
�̖ʐ�S�����������Ƃ����s��������邱�Ƃ��ł��܂��B
�܂��A�Ȑ�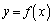 �����ɓʂł��邱�Ƃ���A����PA��̓_�͋Ȑ�
�����ɓʂł��邱�Ƃ���A����PA��̓_�͋Ȑ�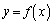 �����ɂ���A����AQ��̓_�͋Ȑ�
�����ɂ���A����AQ��̓_�͋Ȑ�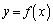 �����ɂ���A�ʐ�T�́A�O�p�`PAB�̖ʐςƎO�p�`QAB�̖ʐς̘a�A�܂�A���s�l�ӌ`
�����ɂ���A�ʐ�T�́A�O�p�`PAB�̖ʐςƎO�p�`QAB�̖ʐς̘a�A�܂�A���s�l�ӌ`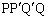 �̖ʐ�S��
�̖ʐ�S��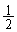 �����傫���Ƃ����s��������邱�Ƃ��ł��܂��B�]���āA
�����傫���Ƃ����s��������邱�Ƃ��ł��܂��B�]���āA �� 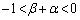 ����ŇB�������܂����B����PQ�̒��_R�͑�2�ی��ɂ���A
����ŇB�������܂����B����PQ�̒��_R�͑�2�ی��ɂ���A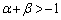 �ł��B
�ł��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B