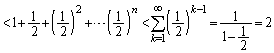��q�嗝�H���w'09�N[1]
�Ɍ��l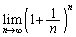 �͎��R�ΐ��̒�e�ł���A���̋ߎ��l��
�͎��R�ΐ��̒�e�ł���A���̋ߎ��l��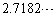 �ł��邱�Ƃ��m���Ă���B�����ł́A
�ł��邱�Ƃ��m���Ă���B�����ł́A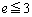 �ł��邱�Ƃ����̎菇�Ŏ������B
�ł��邱�Ƃ����̎菇�Ŏ������B
(1) ���R��k�ɑ��āA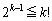 �ł��邱�Ƃ������B
�ł��邱�Ƃ������B (2) 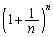 ��藝��p���ēW�J���邱�Ƃɂ��A
��藝��p���ēW�J���邱�Ƃɂ��A �ł��邱�Ƃ������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�Q�l���Ȃǂɂ悭�o�Ă���ؖ�������悢���Ȃ̂ł����A�����A������Ŏ����ł���Ă݂Ȃ����A�ƌ�����ƁA��q���邩���m��܂���B
(�T) 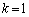 �̂Ƃ��A
�̂Ƃ��A 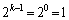 �C
�C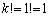
����āA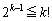 �͐������܂��B
�͐������܂��B (�U) 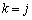 �̂Ƃ��A
�̂Ƃ��A 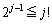 �@����@
�@����@����������Ɖ��肵�܂��B
�@�̗��ӂ�2�������āA
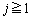 �̂Ƃ��A
�̂Ƃ��A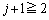 ���A
���A����āA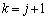 �̂Ƃ��ɂ��A
�̂Ƃ��ɂ��A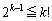 ���������܂��B
���������܂��B (�T)�C(�U)���A���R��k�ɑ��āA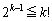 �����藧���܂��B
�����藧���܂��B
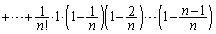 �@����A
�@����A���āA�����ŖڕW�Ƃ��邱�Ƃ́A���ꂪ�A3�ȉ��A�܂�A�擪��1����������2���ȍ~�̘a��2�ȉ��ł��邱�Ƃ��������Ƃł��B
���̂��߂ɁA�A�̑�2���ȍ~�̊e�����A����1�Řa��2�ƂȂ�悤�����䐔���̊e���Ɣ�r�ł��Ȃ����A�l���Ă݂܂��B
����1�C�a��2�ƂȂ�悤���������䋉���̌����r�Ƃ���ƁA �� 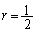 �ƂȂ�̂ŁA�A�̑�
�ƂȂ�̂ŁA�A�̑�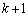 ���A�܂�
���A�܂�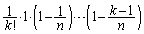 ��
��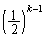 �Ɣ�r���܂��B(1)��p���āA
�Ɣ�r���܂��B(1)��p���āA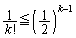 ���A
���A ������
�ƂȂ�̂ŁA�A�̑�2���ȍ~�ɂ��āA
������A��3�����������Ȃ�A
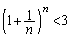 �@����B
�@����B����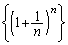 �̊e���ɂ��ćB�����藧�̂ŁA
�̊e���ɂ��ćB�����藧�̂ŁA ���Ɍ��ɂ��āA
���Ɍ��ɂ��āA �����藧���܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B