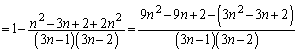九州工大情報数学'09年[4]
箱の中に、数字の1を記入したカード、2を記入したカード、3を記入したカードがそれぞれn枚、合計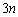 枚入っている。ただし、
枚入っている。ただし、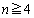 であり、またカードの裏側には何も書かれていないものとする。以下の問いに答えよ。
であり、またカードの裏側には何も書かれていないものとする。以下の問いに答えよ。
(1) 箱の中からカードを1枚取り出し、数字を見ないで伏せておく。次に箱の中から取り出したカードの数字が1である確率を求めよ。
(2) 箱の中から2枚のカードを同時に取り出したとき、カードの数字が異なる確率をnを用いて表せ。
(3) 箱の中から3枚のカードを同時に取り出したとき、カードの数字がちょうど2種類である確率をnを用いて表せ。
(4) 箱の中から4枚のカードを同時に取り出したとき、カードの数字がちょうど2種類である確率をnを用いて表せ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 (2),(3)は余事象に着目してもよいのですが、(4)は余事象を考えてしまうと(3)の応用が効かなくなります。
この問題では、問われている方の事象を考える方が、(2),(3),(4)のつながりがスムーズです。
(1) 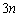 枚のカードから2枚取る取り方は、1枚目の取り方が
枚のカードから2枚取る取り方は、1枚目の取り方が 通り、1枚取ると
通り、1枚取ると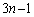 枚残るので、2枚目の取り方が
枚残るので、2枚目の取り方が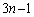 通りで、
通りで、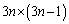 通り。
通り。 1枚目の数字がわからないので、1枚目が1かどうかで場合分けします。
・1枚目に1を取る取り方はn通り、このとき、1は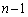 枚残るので、2枚目にも1を取る取り方は
枚残るので、2枚目にも1を取る取り方は 通りで、
通りで、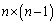 通り。
通り。 ・1枚目に1以外を取る取り方は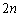 通り、このとき、1はn枚残っていて2枚目に1を取る取り方はn通りで、
通り、このとき、1はn枚残っていて2枚目に1を取る取り方はn通りで、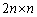 通り。
通り。 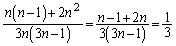 ......[答]
......[答]注.この結果は、1枚目の数字を見ないでおけば、2回目に1を引く確率は、1回目に1を引く確率と同じだということを表しています。
(2) 全事象は(1)と同じく、 通りあります。
通りあります。 1枚目は何を取ってもよいので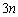 通り。2枚目は1枚目と異なるカードを取ります。1枚目と異なるカードは
通り。2枚目は1枚目と異なるカードを取ります。1枚目と異なるカードは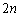 枚あります。
枚あります。
求める確率は、 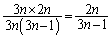 ......[答]
......[答]別解.余事象に着目することもできます。余事象は、1枚目と2枚目が同じ数字になる事象です。全事象は、 枚から2枚取る取り方として
枚から2枚取る取り方として 通り(組み合わせを参照)、1枚目と2枚目が同じになる事象は、同一数字のカードn枚から2枚取る取り方が
通り(組み合わせを参照)、1枚目と2枚目が同じになる事象は、同一数字のカードn枚から2枚取る取り方が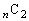 通り、数字は3種類あるので、
通り、数字は3種類あるので、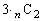 通り、求める確率は、
通り、求める確率は、
(3) 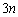 枚のカードから3枚取る取り方は、1枚目が
枚のカードから3枚取る取り方は、1枚目が 通り、2枚目が
通り、2枚目が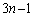 通り、3枚目が
通り、3枚目が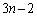 通りで、
通りで、 通り。
通り。 1枚目は何を取ってもよいので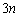 通り。
通り。 ・2枚目に1枚目と同じものを取るとき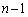 通り、このとき3枚目には、1枚目、2枚目とは異なるものを取ればよいのですが
通り、このとき3枚目には、1枚目、2枚目とは異なるものを取ればよいのですが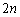 枚残っているので取り方は
枚残っているので取り方は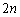 通りあり、
通りあり、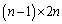 通り。
通り。 ・2枚目に1枚目と異なるものを取るとき 通り、このとき3枚目には、1枚目あるいは2枚目に取ったものと同じものを取ればよいのですが
通り、このとき3枚目には、1枚目あるいは2枚目に取ったものと同じものを取ればよいのですが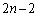 枚残っているので取り方は
枚残っているので取り方は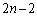 通りあり、
通りあり、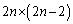 通り。
通り。 求める確率は、
 ......[答]
......[答]別解.余事象は、1〜3枚目が同じ数字になる、か、1〜3枚目で1,2,3の全ての数字が出る事象です。
全事象は、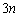 枚から3枚取る取り方として
枚から3枚取る取り方として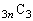 通り。1〜3枚目が同じ数になるのは、同一数字のn枚から3枚取る取り方が
通り。1〜3枚目が同じ数になるのは、同一数字のn枚から3枚取る取り方が 通り、数字が3種類で、
通り、数字が3種類で、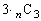 通り。1〜3枚で1,2,3の全ての数字が出るのは、各数字n枚あって、1,2,3の並び方が
通り。1〜3枚で1,2,3の全ての数字が出るのは、各数字n枚あって、1,2,3の並び方が 通りあるので、
通りあるので、 通り。
通り。
求める確率は、 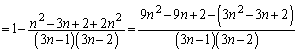
 ......[答]
......[答]
(4) 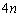 枚のカードから4枚取る取り方は、
枚のカードから4枚取る取り方は、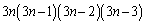 通り。
通り。 1枚目は何を取ってもよいので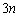 通り。
通り。 ・2枚目に1枚目と同じものを取るとき 通り、このとき、
通り、このとき、 (a) 3枚目に、1枚目、2枚目と同じものを取るとき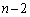 通り、4枚目は、1〜3枚目と異なるものを取るので
通り、4枚目は、1〜3枚目と異なるものを取るので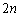 通りで、
通りで、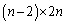 通り。
通り。 (b) 3枚目に、1枚目、2枚目とは異なるものを取るとき 通り、4枚目は、1枚目あるいは3枚目に取ったものと同じものを取ればよいのですが
通り、4枚目は、1枚目あるいは3枚目に取ったものと同じものを取ればよいのですが 枚残っているので取り方は
枚残っているので取り方は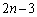 通りあり、
通りあり、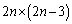 通り。
通り。 (a),(b)合わせて、 通り。
通り。 ・2枚目に1枚目と異なるものを取るとき 通り、このとき、3枚目は、1枚目あるいは2枚目に取ったものと同じものを取ればよく、
通り、このとき、3枚目は、1枚目あるいは2枚目に取ったものと同じものを取ればよく、 通り、4枚目も同様に、
通り、4枚目も同様に、 通りで、
通りで、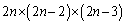 通り。
通り。 求める確率は、
 ......[答]
......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。