���嗝�n���w'09�N�O��[1]
 �C
�C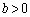 �Ƃ���B�_A
�Ƃ���B�_A �𒆐S�Ƃ��锼�ar�̉~���A�o�Ȑ�
�𒆐S�Ƃ��锼�ar�̉~���A�o�Ȑ�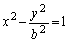 ��2�_B
��2�_B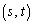 �CC
�CC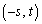 �Őڂ��Ă���Ƃ���B�������A
�Őڂ��Ă���Ƃ���B�������A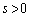 �Ƃ���B�����ŁA�o�Ȑ��Ɖ~���_P�Őڂ���Ƃ́AP���o�Ȑ��Ɖ~�Ƃ̋��L�_�ł���A���_P�ɂ�����o�Ȑ��̐ڐ��Ɠ_P�ɂ�����~�̐ڐ�����v���邱�Ƃł���B
�Ƃ���B�����ŁA�o�Ȑ��Ɖ~���_P�Őڂ���Ƃ́AP���o�Ȑ��Ɖ~�Ƃ̋��L�_�ł���A���_P�ɂ�����o�Ȑ��̐ڐ��Ɠ_P�ɂ�����~�̐ڐ�����v���邱�Ƃł���B
(1) r�Cs�Ct��a��b��p���ĕ\���B
(2) ��ABC�����O�p�`�ƂȂ�a��r�����݂���悤��b�̒l�͈̔͂����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@b�̒l�����낢��ƕς��āA�ǂ������o�Ȑ��̂Ƃ��ɐ��O�p�`���ł��邩����������ł����ƁA(2)�̈Ӗ������߂�ł��傤�B
�_A �𒆐S�Ƃ��锼�ar���~�F
�𒆐S�Ƃ��锼�ar���~�F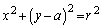 �@����A
�@����A
 ���@�C�A�̋��L�_�ł��邱�Ƃ���A
���@�C�A�̋��L�_�ł��邱�Ƃ���A 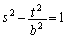 �@����B
�@����B
 �@����C
�@����C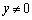 �̂Ƃ��ɂ́A
�̂Ƃ��ɂ́A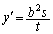 �@����D
�@����D�A��x�Ŕ�������ƁA
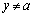 �̂Ƃ��ɂ́A
�̂Ƃ��ɂ́A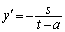 �@����E
�@����E�o�Ȑ��Ɖ~�͓_B �Őڂ���̂ŁA�D�ƇE�͈�v���܂��B
�Őڂ���̂ŁA�D�ƇE�͈�v���܂��B
�� 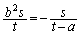 �o�Ȑ��́A
�o�Ȑ��́A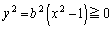 ���A
���A �C
�C �̕����ɑ��݂���̂�
�̕����ɑ��݂���̂�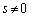 �ł��B����āA
�ł��B����āA 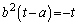
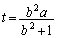 �@����F
�@����F�Ƃ���ŁA �̂Ƃ��A
�̂Ƃ��A �ƇB���
�ƇB���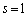 �ł����A
�ł����A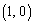 �ɂ�����o�Ȑ��̐ڐ���x���ɐ����Ȓ���
�ɂ�����o�Ȑ��̐ڐ���x���ɐ����Ȓ���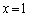 �ł��B
�ł��B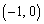 �ɂ�����o�Ȑ��̐ڐ���x���ɐ����Ȓ���
�ɂ�����o�Ȑ��̐ڐ���x���ɐ����Ȓ���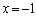 �ł��B
�ł��B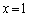 �C
�C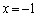 ���~�̐ڐ��ɂȂ�Ƃ��A���S��y���W�F
���~�̐ڐ��ɂȂ�Ƃ��A���S��y���W�F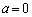 �ƂȂ��Ă��܂����߁A
�ƂȂ��Ă��܂����߁A �Ƃ����������ł́A
�Ƃ����������ł́A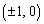 �őo�Ȑ��Ɖ~���ڂ��邱�Ƃ͂���܂���B
�őo�Ȑ��Ɖ~���ڂ��邱�Ƃ͂���܂���B
�܂��A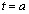 �̂Ƃ��A�~�̐ڐ���x���ɐ����ɂȂ�܂����A�D���A�o�Ȑ��̐ڐ��̌X����
�̂Ƃ��A�~�̐ڐ���x���ɐ����ɂȂ�܂����A�D���A�o�Ȑ��̐ڐ��̌X���� �ŁA�o�Ȑ��̐ڐ���x���ɐ����ł͂Ȃ��A�o�Ȑ��Ɖ~���ڂ��邱�Ƃ͂���܂���B
�ŁA�o�Ȑ��̐ڐ���x���ɐ����ł͂Ȃ��A�o�Ȑ��Ɖ~���ڂ��邱�Ƃ͂���܂���B
�F�̂Ƃ��A �ł��B����āA
�ł��B����āA  ......[��]
......[��]�B���A
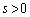 ���A
���A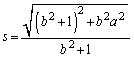 ......[��]
......[��]�C���A
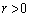 ���A
���A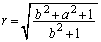 ......[��]
......[��]
(2) ��ABC�����O�p�`�̂Ƃ��A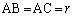 �Ȃ̂ŁA
�Ȃ̂ŁA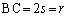 �ł��B����āA
�ł��B����āA 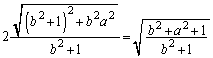
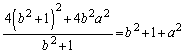

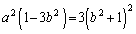
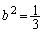 �̂Ƃ����ӂ�0�ł����E�ӂ͐��Ȃ̂�
�̂Ƃ����ӂ�0�ł����E�ӂ͐��Ȃ̂�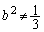 �ł��B
�ł��B
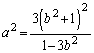 �@����G
�@����G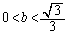 �@����H
�@����H�t�ɇH�����藧�Ƃ��A�G�ɂ����a���߂�A(1)�̌��ʂ�p���āA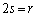 �ƂȂ�悤��r�邱�Ƃ��ł��܂��B
�ƂȂ�悤��r�邱�Ƃ��ł��܂��B
����āA���߂�b�͈̔͂́A  ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 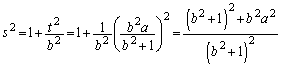
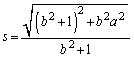 ......[��]
......[��]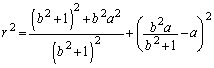
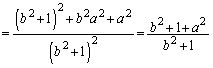
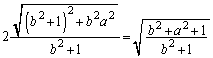
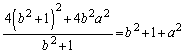
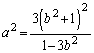 �@����G
�@����G