��㋳��吔�w'09�N[4]
1�̂��������n����Ƃ��Ak��ڂɏo���ڂ� �Ƃ��A�����̐�
�Ƃ��A�����̐� ��
�� �Ƃ���B������
�Ƃ���B������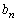 ��r���̎��R���ƂȂ�m����
��r���̎��R���ƂȂ�m���� �Ƃ���B���̖₢�ɓ�����B
�Ƃ���B���̖₢�ɓ�����B
(1) 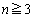 �̂Ƃ��A
�̂Ƃ��A ��n��p���ĕ\���B
��n��p���ĕ\���B (2)(i) 1�̂��������n����Ƃ��A1�ȊO�̖ڂ����傤��s��o��m����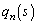 �Ƃ���B
�Ƃ���B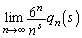 ��s��p���ĕ\���B
��s��p���ĕ\���B (ii) 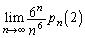 �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(2)(ii)�����ł��B(i)���ǂ����p���邩���|�C���g�ł��B
(1) ���낢��ȍl�������\�ł����A�����ł́A(2)���ɂ��ŁAn������𓊂���Ƃ���1�ȊO�̖ڂ�����o�邩�A�Ƃ������Ƃŕ��ނ��čl���Ă݂����Ǝv���܂��B
 ��1���̎��R���ɂȂ�̂́A�ȉ���4�̏ꍇ�ł��B
��1���̎��R���ɂȂ�̂́A�ȉ���4�̏ꍇ�ł��B(a) n�ׂ�1���o��Ƃ��A1�ʂ�B
(b) 1�ȊO�̖ڂ�1��o��Ƃ��A����1��ɏo���ڂ�2�`6�܂ł�5�ʂ�A2�`6�̖ڂ�n��̂����̂ǂ�1��ɏo�邩��n�ʂ�ŁA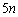 �ʂ肠��܂��B
�ʂ肠��܂��B (c) 1�ȊO�̖ڂ�2��o��Ƃ��A����2��ɏo���ڂ��A
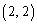 �C
�C �C
�C �C
�C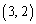 �C
�C �C
�C
��6�ʂ肠��A����2��n��̂����̂ǂ�2�� �ʂ�ŁA
�ʂ�ŁA �ʂ肠��܂��B
�ʂ肠��܂��B(d) 1�ȊO�̖ڂ�3��o��Ƃ��A����3��ɏo���ڂ��A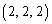 ��1�ʂ�A����3��n��̂����̂ǂ�3��
��1�ʂ�A����3��n��̂����̂ǂ�3��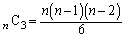 �ʂ肠��܂��B
�ʂ肠��܂��B n������𓊂���Ƃ��A�ڂ̏o���� �ʂ肠���āA���߂��m���́A
�ʂ肠���āA���߂��m���́A 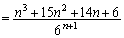 ......[��]
......[��]
(2)(i) 1�ȊO��2�`6��5�ʂ�̖ڂ�s��o��̂� �ʂ�A�P�ȊO�̖ڂ��o��̂�n��̂����̂ǂ�s��
�ʂ�A�P�ȊO�̖ڂ��o��̂�n��̂����̂ǂ�s�� �ʂ�ŁAn������𓊂���1�ȊO�̖ڂ����傤��s��o��m���́A
�ʂ�ŁAn������𓊂���1�ȊO�̖ڂ����傤��s��o��m���́A  ......[��]
......[��](ii) �܂��An�ׂ�1�C���邢�́A1�ȊO�̖ڂ̏o��̂����傤��1��̂Ƃ��ɂ́A ��1���̎��R����2���ɂȂ�܂���B
��1���̎��R����2���ɂȂ�܂���B 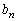 ��2���̎��R���ɂȂ�̂́A�Ⴆ�A1�ȊO�̖ڂ�2��o��Ƃ��A����2��ɏo���ڂ��A
��2���̎��R���ɂȂ�̂́A�Ⴆ�A1�ȊO�̖ڂ�2��o��Ƃ��A����2��ɏo���ڂ��A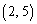 �C
�C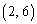 �C
�C �C
�C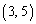 �C
�C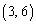 �C
�C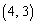 �C
�C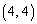 �C
�C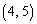 �C
�C �C
�C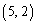 �C
�C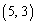 �C
�C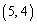 �C
�C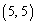 �C
�C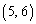 �C
�C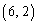 �C
�C �C
�C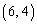 �C
�C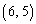 �C
�C
��19�ʂ肠��A����2��n��̂����̂ǂ�2�� �ʂ�ŁA
�ʂ�ŁA �ʂ肠��܂��B
�ʂ肠��܂��B
�ł����A���̂܂܁A1�ȊO�̖ڂ�3��o��Ƃ��A4��o��Ƃ��A�ƁA����Ă����Ƒ�ςȂ��ƂɂȂ�܂��B�����ŁA(i)�̗��p���l���܂��B
�ƌ����Ă��A�ǂ����p����̂��A�Ȃ��Ȃ��v�������т܂���B��C�Â��������Ƃ́A1�ȊO�̖ڂ��o��͂����瑽���Ă��ǂ��킯�ł͂Ȃ��A�Ƃ������Ƃł��B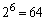 �C
�C ����l����ƁA1�ȊO�̖ڂ�7��ȏ�o�Ă��܂��ƁA
����l����ƁA1�ȊO�̖ڂ�7��ȏ�o�Ă��܂��ƁA �ƂȂ��Ă��܂��܂��B�]���āA
�ƂȂ��Ă��܂��܂��B�]���āA ��2���̎��R���ɂȂ邽�߂ɂ́A1�ȊO�̖ڂ̏o��́A2�A3�A4�A5�A6��̂����ꂩ�łȂ���Ȃ�Ȃ��̂ł��B
��2���̎��R���ɂȂ邽�߂ɂ́A1�ȊO�̖ڂ̏o��́A2�A3�A4�A5�A6��̂����ꂩ�łȂ���Ȃ�Ȃ��̂ł��B
�����ŁA��L��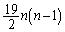 �ʂ�̏ꍇ���l����ƁA���̖ڂ̏o���̏W���́A1�ȊO�̖ڂ�2��o��ꍇ�̖ڂ̏o���̏W���̕����W���ł��B�Ƃ������Ƃ́An������𓊂��āA1�ȊO�̖ڂ�2��o�āA���A
�ʂ�̏ꍇ���l����ƁA���̖ڂ̏o���̏W���́A1�ȊO�̖ڂ�2��o��ꍇ�̖ڂ̏o���̏W���̕����W���ł��B�Ƃ������Ƃ́An������𓊂��āA1�ȊO�̖ڂ�2��o�āA���A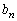 ��2���̎��R���ƂȂ�m����
��2���̎��R���ƂȂ�m����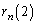 �Ƃ���ƁA
�Ƃ���ƁA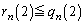 �ɂȂ�Ƃ������Ƃł��B
�ɂȂ�Ƃ������Ƃł��B
����Ɍ����A �Ƃ��āAn������𓊂��āA1�ȊO�̖ڂ�s��o�āA���A
�Ƃ��āAn������𓊂��āA1�ȊO�̖ڂ�s��o�āA���A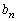 ��2���̎��R���ƂȂ�m����
��2���̎��R���ƂȂ�m����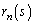 �Ƃ���ƁA
�Ƃ���ƁA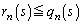 �ƂȂ�܂��B����ŁA(i)�����p�ł������ł��Bn������𓊂��āA
�ƂȂ�܂��B����ŁA(i)�����p�ł������ł��Bn������𓊂��āA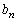 ��2���̎��R���ɂȂ�m��
��2���̎��R���ɂȂ�m�� �́A
�́A 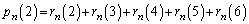 �@����A
�@����A�Ȃ̂ŁA
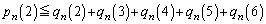 �@����B
�@����B�ł��B����ŁA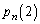 ���̂����߂�͓̂���Ă��A
���̂����߂�͓̂���Ă��A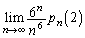 �́A�͂��݂����ɂ���̂��낤�A�Ƃ������̍\�}�����ڂ낰�Ɍ����Ă��܂��B
�́A�͂��݂����ɂ���̂��낤�A�Ƃ������̍\�}�����ڂ낰�Ɍ����Ă��܂��B
�B�� ��������ƁA�E�ӂ́A�@��p���āA
��������ƁA�E�ӂ́A�@��p���āA  �@����C
�@����C������ �Ƃ���ƁA
�Ƃ���ƁA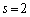 �̍�����
�̍�����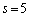 �̍��ł�
�̍��ł�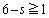 �ƂȂ蕪���n���]�v�ɂ���̂�
�ƂȂ蕪���n���]�v�ɂ���̂� �ƂȂ�܂����A
�ƂȂ�܂����A �̍����������n���c�炸
�̍����������n���c�炸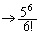 �ƂȂ�A
�ƂȂ�A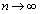 �̂Ƃ��ɁA�B�̉E�ӂ�
�̂Ƃ��ɁA�B�̉E�ӂ� �ƂȂ邱�Ƃ��킩��܂��B������ƌ����āA
�ƂȂ邱�Ƃ��킩��܂��B������ƌ����āA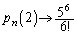 �ł͂Ȃ��A
�ł͂Ȃ��A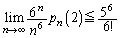 �ł��邱�Ƃɒ��ӂ��Ă��������B
�ł��邱�Ƃɒ��ӂ��Ă��������B
�����ŁA���x�́A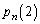 �����������Ȃ���̂�T���܂��B����������ɂ͒T���Ȃ��̂ŁA�܂��A�C��
�����������Ȃ���̂�T���܂��B����������ɂ͒T���Ȃ��̂ŁA�܂��A�C��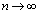 �̂Ƃ��ɗL���Ȋ�^�����鍀��
�̂Ƃ��ɗL���Ȋ�^�����鍀�� �̍������Ƃ����Ƃ���ɖڂ�t���܂��B����́A
�̍������Ƃ����Ƃ���ɖڂ�t���܂��B����́A �Ŋ����ċɌ����Ƃ邩��ŁA
�Ŋ����ċɌ����Ƃ邩��ŁA ��6�̘A�������̐ς��o�Ă���
��6�̘A�������̐ς��o�Ă���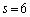 �̍����L���ɂȂ�̂ł��B�����ŁA
�̍����L���ɂȂ�̂ł��B�����ŁA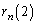 �`
�` �̒��ŁA
�̒��ŁA �Ŋ����ċɌ����Ƃ�Ƃ��ɗL���ɂȂ肻����
�Ŋ����ċɌ����Ƃ�Ƃ��ɗL���ɂȂ肻����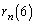 ���l���Ă݂܂��B�A�ɂ����āA
���l���Ă݂܂��B�A�ɂ����āA �̂Ƃ���
�̂Ƃ���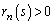 �ł��邱�Ƃ͖��炩�Ȃ̂ŁA
�ł��邱�Ƃ͖��炩�Ȃ̂ŁA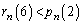 �ł��B
�ł��B
 �́An������𓊂��āA1�ȊO�̖ڂ�6��o�āA���A
�́An������𓊂��āA1�ȊO�̖ڂ�6��o�āA���A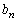 ��2���̎��R���ɂȂ�m���ł��B����6��̖ڂ̏o���́A
��2���̎��R���ɂȂ�m���ł��B����6��̖ڂ̏o���́A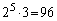 �C
�C �C
�C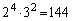 �Ȃǂ���l���āA
�Ȃǂ���l���āA  �C
�C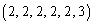
��2�ʂ肵������܂���B
 �̕��́An��̂����ǂ�6���2���o�邩�ƍl���āA
�̕��́An��̂����ǂ�6���2���o�邩�ƍl���āA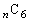 �ʂ�A
�ʂ�A
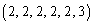 �̕��́An��̂����ǂ�6���2��3���o�邩��
�̕��́An��̂����ǂ�6���2��3���o�邩�� �ʂ�A6��̂����ǂ̉�3����6�ʂ�ŁA
�ʂ�A6��̂����ǂ̉�3����6�ʂ�ŁA �ʂ�A
�ʂ�A
�� 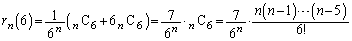
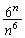 �������āA
�������āA �Ƃ���ƁA
�Ƃ���ƁA 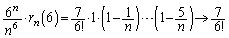 �@����D
�@����D���̋Ɍ��l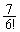 �́A��قLJC�̉E�ӂ�
�́A��قLJC�̉E�ӂ�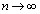 �Ƃ����Ƃ��̋Ɍ��l
�Ƃ����Ƃ��̋Ɍ��l �ƐH������Ă��܂��B�B�̂܂܂ł́A�͂��݂����̌`�ɂł��Ȃ��̂ł��B
�ƐH������Ă��܂��B�B�̂܂܂ł́A�͂��݂����̌`�ɂł��Ȃ��̂ł��B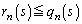 �Ȃ̂ŁA�B�̉E�ӂ̂���������
�Ȃ̂ŁA�B�̉E�ӂ̂���������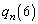 ��
�� �Ƃ��Ă��A
�Ƃ��Ă��A �ƂȂ�܂��B�����ŁA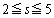 �̂Ƃ��A
�̂Ƃ��A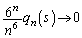 �ł��������Ƃ��v���N�����A�͂��݂����̌`������ꂽ���Ƃ��킩��Ǝv���܂��B���ǁA
�ł��������Ƃ��v���N�����A�͂��݂����̌`������ꂽ���Ƃ��킩��Ǝv���܂��B���ǁA  �@����A
�@����A�ɂ����āA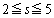 �̂Ƃ�
�̂Ƃ�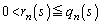 �ł��邱�Ƃ���A
�ł��邱�Ƃ���A 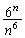 �������āA
�������āA�����ŁA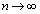 �Ƃ���ƁA�D�ƁA
�Ƃ���ƁA�D�ƁA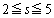 �̂Ƃ�
�̂Ƃ�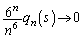 �ł��邱�Ƃ���A���ӁA�E�ӂƂ��A
�ł��邱�Ƃ���A���ӁA�E�ӂƂ��A 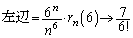 �C
�C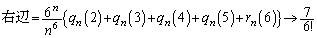
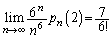 ......[��]
......[��]�NjL�D�\���Z�u�t�̂悤�ȃv���Ȃ�ŏ����� ���x�z�I���낤�Ƃ������ƂɋC�Â��Ǝv���܂����A��ʂ̎��̊F����́A���낢��Ǝ��s���낵�čŏI�ɂ��ǂ���̂ō\��Ȃ��Ǝv���܂��B
���x�z�I���낤�Ƃ������ƂɋC�Â��Ǝv���܂����A��ʂ̎��̊F����́A���낢��Ǝ��s���낵�čŏI�ɂ��ǂ���̂ō\��Ȃ��Ǝv���܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 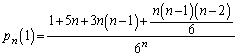
 ......[��]
......[��] �@����C
�@����C