阪大文系数学'09年[3]
次のような、いびつなさいころを考える。1,2,3の目が出る確率はそれぞれ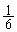 ,4の目が出る確率はa,5,6の目が出る確率はそれぞれ
,4の目が出る確率はa,5,6の目が出る確率はそれぞれ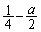 である。ただし、
である。ただし、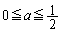 とする。
とする。
このさいころを振ったとき、平面上の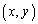 にある点Pは、1,2,3のいずれかの目が出ると
にある点Pは、1,2,3のいずれかの目が出ると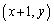 に、4の目が出ると
に、4の目が出ると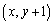 に、5,6のいずれかの目が出ると
に、5,6のいずれかの目が出ると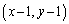 に移動する。
に移動する。
原点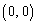 にあった点Pが、k回さいころを振ったときに
にあった点Pが、k回さいころを振ったときに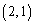 にある確率を
にある確率を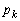 とする。
とする。
(2) 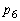 を求めよ。
を求めよ。 (3) 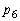 が最大になるときのaの値を求めよ。
が最大になるときのaの値を求めよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 確率と3次関数の融合問題です。(2)の考え方は定型的なものなので、記憶するようにしてください。
(1) 原点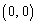 にあった点Pが1回さいころを振って行ける可能性のある点は、
にあった点Pが1回さいころを振って行ける可能性のある点は、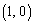 ,
,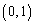 ,
,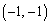 で
で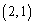 に行ける可能性はありません。よって、
に行ける可能性はありません。よって、 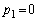 ......[答]
......[答]同様に考えて、原点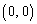 にあった点Pが2回さいころを振って行ける可能性のある第1象限の点は
にあった点Pが2回さいころを振って行ける可能性のある第1象限の点は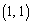 のみで、
のみで、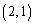 に到達できる可能性はありません。よって、
に到達できる可能性はありません。よって、 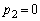 ......[答]
......[答]原点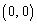 にあった点Pが3回さいころを振って
にあった点Pが3回さいころを振って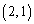 に到達するのは、1,2,3のいずれかの目が2回、4の目が1回出たときで、3回の目の出方が
に到達するのは、1,2,3のいずれかの目が2回、4の目が1回出たときで、3回の目の出方が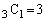 通りあります。よって、
通りあります。よって、 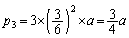 ......[答]
......[答]
(2) 樹形図を書いて場合の数を数えようとすると大変なことになります。
こうした問題では、それぞれの事象の起こる回数に関する等式(不等式ということもあります)を立てます。
6回さいころを振るとき、1,2,3の目が出る(x座標が1増える)回数をiとし、4の目が出る(y座標が1増える)回数をjとし、5,6の目が出る(x座標とy座標が)回数をkとして、
x座標について、
y座標について、
これらを満たすi,j,kは、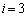 ,
,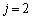 ,
,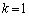 6回さいころを振るとき、1,2,3の目が3回出て、4の目が2回出て、5,6の目が1回出る目の出方のパターンは、
6回さいころを振るとき、1,2,3の目が3回出て、4の目が2回出て、5,6の目が1回出る目の出方のパターンは、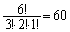 通り(同じものを含む順列を参照)あり、その確率
通り(同じものを含む順列を参照)あり、その確率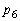 は、
は、 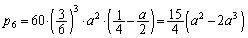 ......[答]
......[答]
(3) 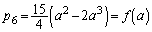
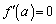 とすると、
とすると、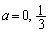 a,0,,
a,0,,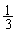 ,,
,,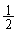
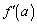 ,0,+,0,−,
,0,+,0,−,
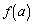 ,,
,, ,,
,, ,増減表より(3次関数の増減を参照)、
,増減表より(3次関数の増減を参照)、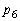 が最大になるときのaの値は、
が最大になるときのaの値は、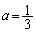 ......[答]
......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。