��嗝�n���w'09�N���[3]
O�����_�Ƃ���xyz��ԓ��̓_A�CB�CC�����ꂼ��A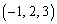 �CB
�CB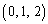 �CC
�CC �Ƃ��A2�_A�CB��ʂ钼����
�Ƃ��A2�_A�CB��ʂ钼���� �Ƃ���B�ȉ��̖₢�ɓ�����B
�Ƃ���B�ȉ��̖₢�ɓ�����B
(1) �_P�͒���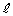 ����A�_Q��y��������̂Ƃ���B���̂Ƃ��A2�_P��Q�Ƃ̋����̍ŏ��l�����߂�B�܂��AP��Q�Ƃ̋������ŏ��ƂȂ�Ƃ���P��Q�����ꂼ��
����A�_Q��y��������̂Ƃ���B���̂Ƃ��A2�_P��Q�Ƃ̋����̍ŏ��l�����߂�B�܂��AP��Q�Ƃ̋������ŏ��ƂȂ�Ƃ���P��Q�����ꂼ��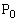 �C
�C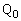 �Ƃ���B
�Ƃ���B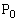 ��
�� �̍��W�����߂�B
�̍��W�����߂�B (2) 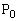 �Ƃ̋�����s�ł���悤�Ȓ���
�Ƃ̋�����s�ł���悤�Ȓ���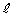 ��̓_�̈��S�Ƃ���B�_S����O�p�`
��̓_�̈��S�Ƃ���B�_S����O�p�`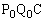 ���܂ޕ��ʂɉ��낵�������Ƃ��̕��ʂƂ̌�_��R�Ƃ���Ƃ��A����SR�̒��������߂�B
���܂ޕ��ʂɉ��낵�������Ƃ��̕��ʂƂ̌�_��R�Ƃ���Ƃ��A����SR�̒��������߂�B (3) y����ɒ���k�̐���DE������A���� ��ɒ���m�̐���FG������B�l�ʑ�DEFG�̑̐ς����߂�B
��ɒ���m�̐���FG������B�l�ʑ�DEFG�̑̐ς����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�˂���̈ʒu�ɂ���2����������̒�����2�̐����������Ƃ��A2�����̒[�_��4���_�Ƃ����l�ʑ̂̑̐������ɂȂ邱�Ƃ������A�Ƃ������ł��B�Ȃ��A��ԃx�N�g�����Q�Ƃ��Ă��������B
(1) 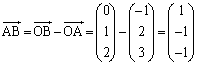
 �@����@
�@����@y����̓_Q�̍��W��q�������Ƃ���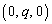 �@����A
�@����A ����́A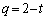 ����
����  �̂Ƃ��ɍŏ��l2�ƂȂ�܂��B
�̂Ƃ��ɍŏ��l2�ƂȂ�܂��B
����āA2�_P�CQ�̋����̍ŏ��l�́A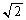 ......[��]�܂��AP�CQ�̋����̍ŏ���^����
......[��]�܂��AP�CQ�̋����̍ŏ���^����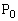 �C
�C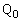 �̍��W�́A
�̍��W�́A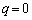 �C
�C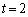 ���@�C�A�ɑ�����āA
���@�C�A�ɑ�����āA 
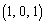 �C
�C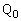
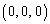 ......[��]�@(�܂�
......[��]�@(�܂�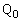 �͌��_O�ł�)
�͌��_O�ł�)�ʉ��D�{��ł�Q��y����̓_�ō��W���ȒP�Ȃ̂ŁA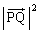 ��2����t�Cq�ŕ\���Ă��債���v�Z�ɂ͂Ȃ�܂��A
��2����t�Cq�ŕ\���Ă��債���v�Z�ɂ͂Ȃ�܂��A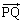 �̊e������2������������悤�ȂƂ��ɂ͌v�Z�����ɖʓ|�ɂȂ�܂��B�˂���̈ʒu�ɂ���2����������_�Ԃ̋����̍ŏ��l�����߂�ꍇ�ɂ́A���ʂ̕������𗘗p���Ĉȉ��̂悤�ɉ��邱�Ƃ��ł��܂��B
�̊e������2������������悤�ȂƂ��ɂ͌v�Z�����ɖʓ|�ɂȂ�܂��B�˂���̈ʒu�ɂ���2����������_�Ԃ̋����̍ŏ��l�����߂�ꍇ�ɂ́A���ʂ̕������𗘗p���Ĉȉ��̂悤�ɉ��邱�Ƃ��ł��܂��B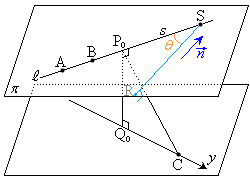 y���ɕ��s�Œ���
y���ɕ��s�Œ��� ���܂ޕ���π�̖@���x�N�g���́Ay���ɂ�����
���܂ޕ���π�̖@���x�N�g���́Ay���ɂ����� �ɂ������A�܂�A�x�N�g��
�ɂ������A�܂�A�x�N�g��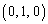 �ɂ�
�ɂ� �ɂ������ł��B���҂��O���́A
�ɂ������ł��B���҂��O���́A �ƂȂ�̂ŁA����π�̖@���x�N�g�� ��
��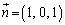 �Ƃ��āA����π�̕������́A
�Ƃ��āA����π�̕������́A 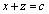 �@(c�͒萔)
�@(c�͒萔)�ƂȂ�܂��B����π�́A�_A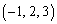 ��ʂ�̂ŁA
��ʂ�̂ŁA 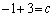 �@��
�@�� 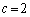
������A����π�̕������́A
2�_P�CQ�̍ŏ��l�́Ay����̔C�ӂ̓_(�ǂ̓_�ł�����π�Ƃ̋����͓����ł�)�A�Ⴆ�Ό��_�ƕ���π�Ƃ̋����ƂȂ�A�_�ƕ��ʂ̋����̌�����p���āA
����ŁA�ȒP�ɍŏ��l�����߂��܂����A���̉�@�ł́A�ŏ��l��^����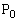 �C
�C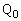 �̍��W�����߂��܂���B
�̍��W�����߂��܂���B
�����ŁAP�CQ�̋������ŏ��ɂȂ�Ƃ��ɁA ��y���ɂ�����
��y���ɂ�����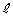 �ɂ������ɂȂ�Ƃ��������𗘗p���܂��B
�ɂ������ɂȂ�Ƃ��������𗘗p���܂��B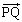 �́A��L�̂悤�ɂ��ē���ꂽ
�́A��L�̂悤�ɂ��ē���ꂽ �ɕ��s�ɂȂ�̂ŁA����k��p���āA
�ɕ��s�ɂȂ�̂ŁA����k��p���āA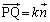 �Ƃ����܂��B�@�C�A��p���āA
�Ƃ����܂��B�@�C�A��p���āA ������A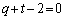 �C
�C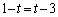
��  �C
�C
����ŁA �C
�C �̍��W�����߂��܂��B
�̍��W�����߂��܂��B
(2) �_S����O�p�`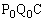 ���܂ޕ��ʂɉ��낵�������Ƃ��̕��ʂƂ̌�_��R�Ƃ���A�Ƃ������Ƃ́A
���܂ޕ��ʂɉ��낵�������Ƃ��̕��ʂƂ̌�_��R�Ƃ���A�Ƃ������Ƃ́A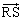 �́A
�́A �ɂ�
�ɂ� �ɂ��������Ƃ������Ƃł��B
�ɂ��������Ƃ������Ƃł��B �Ƃ����ƁA
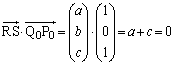
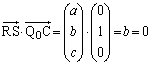 ������A
������A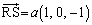 �Ƃ����܂��B
�Ƃ����܂��B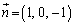 �C
�C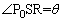 �Ƃ��āA
�Ƃ��āA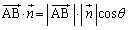
����āA
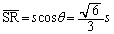 ......[��]
......[��]
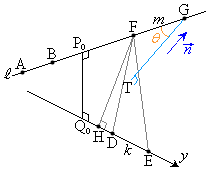 (3) F���y���ɐ���FH�����낵�AH��y���W��u�Ƃ���ƁAF��y���W��u�ł��B�@���A
(3) F���y���ɐ���FH�����낵�AH��y���W��u�Ƃ���ƁAF��y���W��u�ł��B�@���A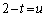 �Ƃ����ƁA
�Ƃ����ƁA
F��x���W�Az���W�́A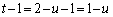 �C
�C ���AF�̍��W��
���AF�̍��W��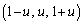 D��y���W��w�Ƃ����D�̍��W��
D��y���W��w�Ƃ����D�̍��W��
G����O�p�`DEF���܂ޕ��ʂɐ���GT�����낷�ƁA ��y���ɂ�
��y���ɂ�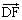 �ɂ������ŁA
�ɂ������ŁA
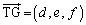
�Ƃ����ƁA ������A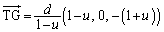 �Ƃ����܂��B
�Ƃ����܂��B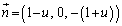 �C
�C �Ƃ��āA
�Ƃ��āA
 �C
�C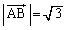 �C
�C ���A
���A ���A�O�p�`DEF�̖ʐς́A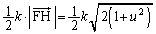
�l�ʑ�DEFG�̑̐ς́A������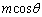 �ŁA
�ŁA 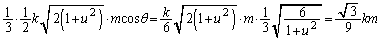 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 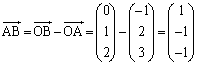
 �@����@
�@����@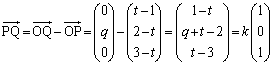
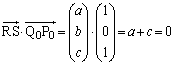
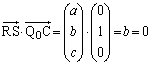
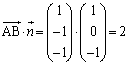 �C
�C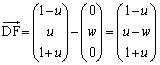

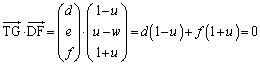
 �C
�C
