��Ԃɂ�����2�����̈ʒu�W�@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
 ���̍��ڂɂ��ẮA��ԃx�N�g�����Q�Ƃ��Ă��������B
���̍��ڂɂ��ẮA��ԃx�N�g�����Q�Ƃ��Ă��������B
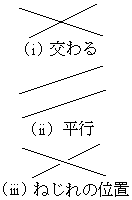
��Ԃɂ�����2�����̈ʒu�W�́A�E�}�̂悤��
(i) �����@(ii) ���s�@(iii) �˂���̈ʒu
��3�ʂ�B
(i) ��Ԃɂ�����2����
l�F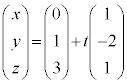 �@����@m�F
�@����@m�F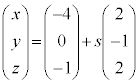 �@����A
�@����A �́A�@���A�A����x�Cy�Cz�����Ƃ����ƁA
�B�ƇC����A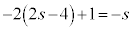
�� 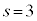
�B���A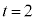
�ƂȂ�̂ł����A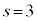 �C
�C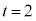 �́A�D�����܂��B
�́A�D�����܂��B
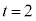 �̂Ƃ��A�@�ł́A
�̂Ƃ��A�@�ł́A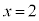 �C
�C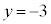 �C
�C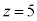
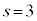 �̂Ƃ��A�A�ł��A
�̂Ƃ��A�A�ł��A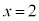 �C
�C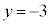 �C
�C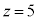
�ƂȂ�܂��B
�Ƃ������Ƃ́A����l�Cm�Ƃ��ɁA�_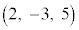 ��ʂ�Ƃ������Ƃł����āA2����l�Cm�́A�_
��ʂ�Ƃ������Ƃł����āA2����l�Cm�́A�_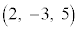 �ɂ����Č����Ƃ������Ƃ��Ӗ����܂��B
�ɂ����Č����Ƃ������Ƃ��Ӗ����܂��B
��Ԃɂ����镽�s�łȂ�2�����́A�K��������_�������܂���B
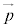 �C
�C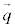 ��l�Cm����_�̈ʒu�x�N�g���A
��l�Cm����_�̈ʒu�x�N�g���A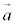 �C
�C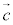 ��l�Cm���1��_�̈ʒu�x�N�g���A
��l�Cm���1��_�̈ʒu�x�N�g���A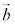 �C
�C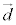 ��l�Cm�̕����x�N�g��(
��l�Cm�̕����x�N�g��(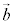 �C
�C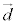 ��1���Ɨ�)�At�Cs���������Ƃ��āA2����l�Cm���x�N�g�����������A
��1���Ɨ�)�At�Cs���������Ƃ��āA2����l�Cm���x�N�g�����������A
l�F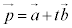 m�F
m�F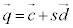
�ƕ\�����Ƃ��܂��B
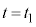 �C
�C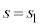 �ɂȂ����Ƃ���
�ɂȂ����Ƃ���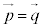 �ƂȂ�A2����l�Cm��
�ƂȂ�A2����l�Cm��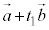 ���ʒu�x�N�g���Ƃ���_�Ō����A�Ƃ��܂��B���̂Ƃ��A
���ʒu�x�N�g���Ƃ���_�Ō����A�Ƃ��܂��B���̂Ƃ��A
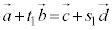 �@����E
�@����E
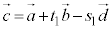 �@����F
�@����F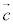 ���ʒu�x�N�g���Ƃ���_���A�x�N�g��������(���ʂ̃x�N�g�����������Q��)
���ʒu�x�N�g���Ƃ���_���A�x�N�g��������(���ʂ̃x�N�g�����������Q��)
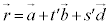 �@����G
�@����G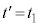 �C
�C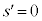 �Ƃ����Ƃ���
�Ƃ����Ƃ���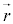 ���ʒu�x�N�g������_��2����l�Cm�̌�_�ł��B�܂��A�G��
���ʒu�x�N�g������_��2����l�Cm�̌�_�ł��B�܂��A�G��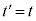 �C
�C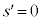 �Ƃ���ƒ���l�ƂȂ�A�G��
�Ƃ���ƒ���l�ƂȂ�A�G��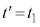 �C
�C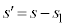 �Ƃ���ƁA�F��p���āA
�Ƃ���ƁA�F��p���āA
�́A����m�ł��B�܂�A����α�́A�����2����l�Cm���܂ޕ��ʂł��B
�����ŁA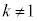 �C
�C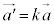 �Ƃ��āA
�Ƃ��āA
�Ƃ���ƁA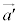 �C
�C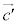 ���ʒu�x�N�g���Ƃ���_�͕���α��̓_�ł͂Ȃ��A
���ʒu�x�N�g���Ƃ���_�͕���α��̓_�ł͂Ȃ��A
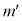 �F
�F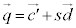
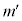 ��l�ƌ�_�������܂���(��q)�B
��l�ƌ�_�������܂���(��q)�B
l�Cm���@�C�A�̏ꍇ�A�G�́A
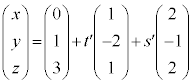 �@����H
�@����H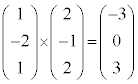 �ƂȂ�̂ŁA�H�̗��ӂ�
�ƂȂ�̂ŁA�H�̗��ӂ� �Ƃ̓��ς��Ƃ邱�Ƃɂ�蕽��α�̕������́A
�Ƃ̓��ς��Ƃ邱�Ƃɂ�蕽��α�̕������́A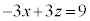 �C�܂�A
�C�܂�A
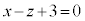 �@����I
�@����I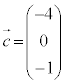 �́A�I�����̂ŕ���α��̓_�ł���Al�Cm�͂Ƃ��ɕ���α��̒����ł��B
�́A�I�����̂ŕ���α��̓_�ł���Al�Cm�͂Ƃ��ɕ���α��̒����ł��B
(ii)�@��Ԃɂ�����2���������s�ł����Ă��A����̒����łȂ��ꍇ�A����2�����͌�_�������܂���B
(iii) ��Ԃɂ�����2����
l�F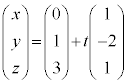 �@����J
�@����J
m�F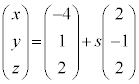 �@����K
�@����K
�́A�J���A�K����x�Cy�Cz�����Ƃ����ƁA
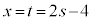 �@����L
�@����L
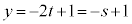 �@����M
�@����M
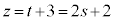 �@����N
�@����N
�L�ƇM����A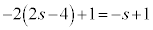
�� 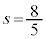
�L���A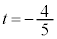
�ł����A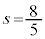 �C
�C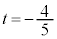 �͇N�������܂���B
�͇N�������܂���B
�܂�A����l��̓_�ƒ���m��̓_������̓_�ɂȂ邱�Ƃ͂��蓾�Ȃ��̂ł��B����́A����2��������_�������Ȃ����Ƃ��Ӗ����܂��B���̂悤��2�����̈ʒu�W���u�˂���̈ʒu�v�ƌ����܂��B
l��̓_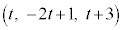 ��m��̓_
��m��̓_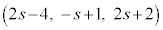 �Ƃ̋���d���l���Ă݂܂��B
�Ƃ̋���d���l���Ă݂܂��B
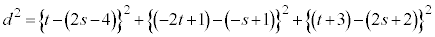
�@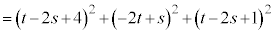 �@����O
�@����O
�E�ӂ�W�J���Đ�������ƁA
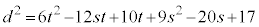
�����t�Ɋւ���2�����ƌ���������������ƁA
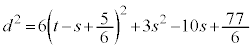
����ɁA�c��̕�����s�ɂ��Ă�������������ƁA
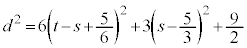
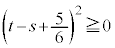 �C
�C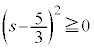 �ł�����A
�ł�����A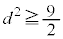 �ƂȂ�܂��B�ł�����A2����l�Cm��̓_�͂����Ƃ��߂��_���u�̋�����
�ƂȂ�܂��B�ł�����A2����l�Cm��̓_�͂����Ƃ��߂��_���u�̋�����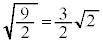 �ł����āA���������2�����������Ȃ����Ƃ��킩��܂��B
�ł����āA���������2�����������Ȃ����Ƃ��킩��܂��B
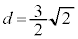 �ƂȂ�̂́A
�ƂȂ�̂́A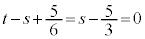 �C�܂�A
�C�܂�A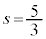 �C
�C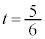 �̂Ƃ��ł��B
�̂Ƃ��ł��B
���̂Ƃ��A�J���A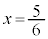 �C
�C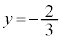 �C
�C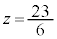
�K���A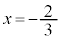 �C
�C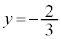 �C
�C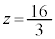
l��̓_��m��̓_�Ƃ̋����̍ŏ��l��^����2�_�́Al���P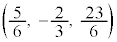 ��m���Q
��m���Q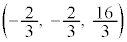 �ł��B
�ł��B
�����ŁA����2�_�����ԃx�N�g��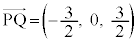 �́Al�Cm�̕����x�N�g��
�́Al�Cm�̕����x�N�g��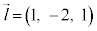 �C
�C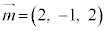 �ɑ��āA
�ɑ��āA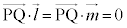
�܂�A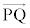 �́A����l�C����m�̑o���Ɛ����ł��B
�́A����l�C����m�̑o���Ɛ����ł��B
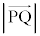 ��2����l�Cm�������ƌ������Ƃ�����܂��B
��2����l�Cm�������ƌ������Ƃ�����܂��B
�܂��A2����l�Cm�̕����x�N�g��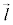 �C
�C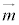 �̂Ȃ��p���A2����l�Cm�̂Ȃ��p�ƌ������Ƃ�����܂��B
�̂Ȃ��p���A2����l�Cm�̂Ȃ��p�ƌ������Ƃ�����܂��B
�Ƃ���ŁA�@�C�A�ŕ\����钼��l�Cm�͌�_�������Ă��܂����B�@�ƇJ�͓���̒����ł����A�A�ƇK�� ��
�� �̂Ƃ��낪����Ă��āA�J�ƇK�͌�_�������܂���B
�̂Ƃ��낪����Ă��āA�J�ƇK�͌�_�������܂���B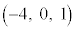 �͇I�����̂ŕ���α��̓_�ł����A
�͇I�����̂ŕ���α��̓_�ł����A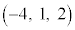 �͇I�����Ȃ��̂ŕ���α��̓_�ł͂Ȃ��A���̂��߂ɕ���α��̒����łȂ��K(�ł����A�K�ƕ���α�͕��s�ł�)�ƇJ�͌�_�������܂���B
�͇I�����Ȃ��̂ŕ���α��̓_�ł͂Ȃ��A���̂��߂ɕ���α��̒����łȂ��K(�ł����A�K�ƕ���α�͕��s�ł�)�ƇJ�͌�_�������܂���B
���D �́A
�́A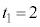 �C
�C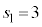 �Ƃ��āA�F��
�Ƃ��āA�F��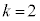 �Ƃ������́A
�Ƃ������́A
�ɂȂ��Ă��܂��B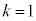 �łȂ��̂ŁA
�łȂ��̂ŁA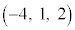 �͕���α��̓_�ɂ͂Ȃ�܂���B
�͕���α��̓_�ɂ͂Ȃ�܂���B 2����l�Cm�̋��������߂�̂ɁAl�Cm��̓_��t�Cs�ŕ\���āAl�Cm��̓_�̋�����2��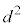 ���O�̂悤�ɕ\���A����������2��s����
���O�̂悤�ɕ\���A����������2��s����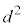 �̍ŏ��l�Ƃ��ċ��߂�̂ł͑�ςł��B��L�ɏ������悤�ɁA�K // α�Ȃ̂ŁA�K��̓_�A�Ⴆ�A�K��
�̍ŏ��l�Ƃ��ċ��߂�̂ł͑�ςł��B��L�ɏ������悤�ɁA�K // α�Ȃ̂ŁA�K��̓_�A�Ⴆ�A�K��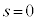 �Ƃ����_
�Ƃ����_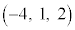 �ƕ���α�F
�ƕ���α�F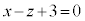 (�I)�Ƃ̋����Ƃ��āA
(�I)�Ƃ̋����Ƃ��āA
���A�e�Ղɋ��߂邱�Ƃ��ł��܂��B
�܂�A�˂���̈ʒu�ɂ���2�����̋��������߂�ɂ́A2�����̕����x�N�g���̊O��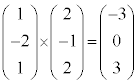 ��@���x�N�g���Ƃ��镽��α���A�����J���܂ݒ����K�ƕ��s�ȕ��ʂƂ��āA����α�̕��������A
��@���x�N�g���Ƃ��镽��α���A�����J���܂ݒ����K�ƕ��s�ȕ��ʂƂ��āA����α�̕��������A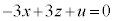 �Ƃ����āA�J��̓_
�Ƃ����āA�J��̓_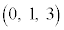 �������āA
�������āA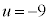 �����߁A�K��̓_
�����߁A�K��̓_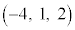 �ƕ���α�Ƃ̋����Ƃ��ċ��߂�悢�A�Ƃ������ƂɂȂ�܂��B
�ƕ���α�Ƃ̋����Ƃ��ċ��߂�悢�A�Ƃ������ƂɂȂ�܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 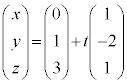 �@����@
�@����@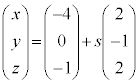 �@����A
�@����A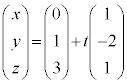 �@����@
�@����@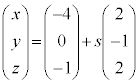 �@����A
�@����A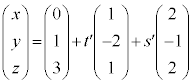 �@����H
�@����H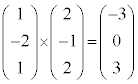 �ƂȂ�̂ŁA�H�̗��ӂ�
�ƂȂ�̂ŁA�H�̗��ӂ�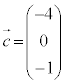 �́A�I�����̂ŕ���α��̓_�ł���Al�Cm�͂Ƃ��ɕ���α��̒����ł��B
�́A�I�����̂ŕ���α��̓_�ł���Al�Cm�͂Ƃ��ɕ���α��̒����ł��B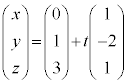 �@����J
�@����J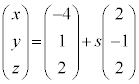 �@����K
�@����K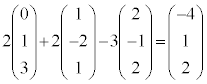
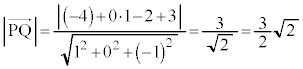
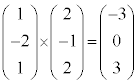 ��@���x�N�g���Ƃ��镽��α���A�����J���܂ݒ����K�ƕ��s�ȕ��ʂƂ��āA����α�̕��������A
��@���x�N�g���Ƃ��镽��α���A�����J���܂ݒ����K�ƕ��s�ȕ��ʂƂ��āA����α�̕��������A