東京理科大理数学'09年[2]
以下の(1)から(3)の問いに答えよ。ただし、(1)および(2)で得られた結論は、必要なら(3)の解答の際に用いてよい。
(1) 
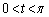をみたす実数tをとる。実数θ が
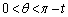の範囲を動くとき、関数
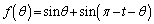の値が最大になるようなθ の値と、関数
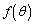の最大値
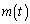を求めよ。 (2) (1)で求めた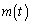
を用いて関数
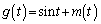を定める。実数tが
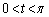の範囲を動くとき、関数
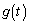の値が最大になるようなtの値と、関数
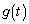の最大値Mを求めよ。 (3) 半径1の円Tに内接する三角形ABCの頂点Aにおける内角をtで表し、頂点Cにおける内角をθ で表すことにする。
(a) 頂点Aにおける内角tが動く範囲を求めよ。
(b) 頂点Aにおける内角tを一定に保ちながら頂点Aが円T上を動くとき、線分ABと線分ACの長さの和が最大になるための必要十分条件を三角形ABCについての条件として述べよ。
(c) (b)で求めた条件をみたす三角形ABCの頂点Aにおける内角tを、(a)で求めた範囲で動かすことにより、この三角形の3辺の長さの和の最大値を求めよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 計算の部分と論述の部分を明確に分けて、受験生の力を評価しよう、という問題です。
(1) 
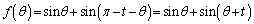
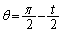......[答]のとき、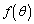
は、 最大値：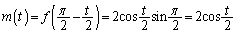
......[答] をとります。
増減表より(関数の増減を参照)、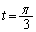
......[答]のとき、
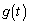は、 最大値：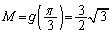
......[答] をとります。
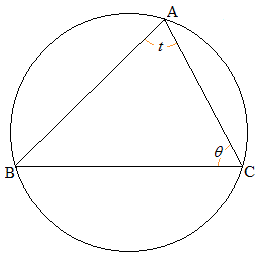
(3)(a)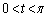 
......[答] ∴ 
，
，
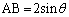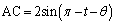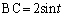
線分ABと線分ACの長さの和は、
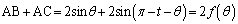(但し、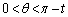
)内角tを固定してθ を動かすと、(1)より、
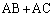は、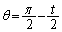
のときに最大値をとりますが、このとき、頂点Bにおける内角は、 となり、頂点Bにおける内角と頂点Cにおける内角が等しくなります。また、頂点Bにおける内角と頂点Cにおける内角が等しければ、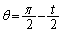
となり、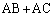
が最大になります。つまり、線分ABと線分ACの長さの和が最大になるための必要十分条件は、
三角形ABCが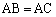
となる二等辺三角形であること ......[答]
(c) 三角形ABCの3辺の長さの和は、 tを固定してθ だけを動かすと、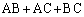
は、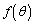
が最大になるとき、つまり、(1)より、
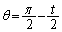のときに、最大値
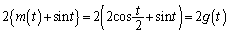をとります。tを
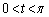の範囲で動かすと、
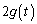は、(2)より、
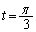のとき、 最大値：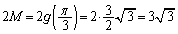
......[答] をとります。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
より、
となるので、
，つまり、
より
とすると、
，即ち、
，
，
